中学数学「比例と反比例」の教え方①　関数とは何か？

中学数学の教え方のノウハウを提供するこの連載。

今回から中１「比例と反比例」です。

いわゆる勉強のしかたではなく、「この単元でつまずいている場合、どのように教えたらいちばん理解が早いのか」という具体的な指導法を書いていきます。

いま、中学生をもつ保護者の方。

塾講師や家庭教師をしている方。

指導に悩む中学校数学教員の方。

参考になればさいわいです。

 

[過去記事一覧]

正負の数①　②　③

文字と式①　②　③　④　⑤

１次方程式①　②　③　④

方程式文章題①　②　③　④　⑤　⑥　⑦　⑧　⑨

 

１回目は「関数とは何か」について。

「比例と反比例」単元では最初にまず、関数の導入がおこなわれます。

教科書および多くの中学校の授業でおこなわれている導入は、たとえばこんな感じです。

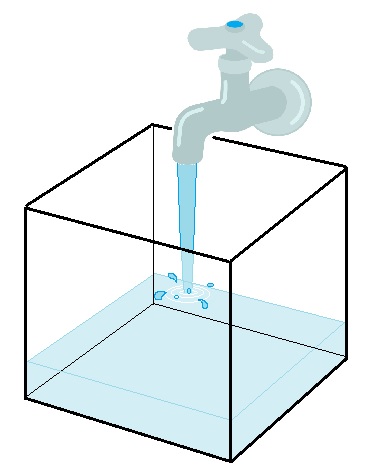
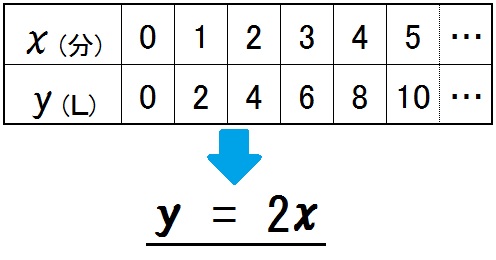
水槽に毎分2Lの割合で水を入れていきます。水を入れはじめてから \(x\) 分後の水の量を \(y\) Lとすると、 \(x\) と \(y\) のあいだにはどんな関係があるでしょうか。

このように、\(y=2x\) という関係があるときの \(x\) と \(y\) のように、いろいろな値をとる文字を変数といいます。

一般に、２つの変数 \(x\) と \(y\) があって、 \(x\) の値を決めると、それに対応して \(y\) の値がただひとつに決まるとき、 \(y\) は \(x\) の関数であるといいます。

このあと中学校では、「次のうち \(y\) が \(x\) の関数であるものはどれか」などの問題が出ます。

ここでつまずく原因。

大別すると２つです。

• 関数とは何か、教える側もちゃんと理解していない
• 抽象化が早すぎる（具体例が少なすぎる）

つまり教える側が、この記述はコーシーによる定義であること、それなのに現代数学ではオイラーによる定義を集合論で拡張した「写像」が関数であることを、ちゃんと理解していない。ようするに関数には２つの定義があることを意識していないのです。

そして、２つの量の関係をみていく際にいきなり \(x\) と \(y\) という文字を使ってしまう。しかも \(y=2x\) と関係を表す式までいきなり文字入りで出してしまう。おまけに具体例がひとつだけなのに「変数」という用語まで定義してしまう。こうした早すぎる抽象化が生徒をおいてけぼりにするのです。

 

そこで本記事ではまず、そもそも関数とは何かをふりかえります。

関数は数学のなかでどんな位置づけの分野なのか？

関数の２つの定義はどうちがうのか？

こうした俯瞰的視野（見通し）を、教師の側がもつことが先決です。

 

そのうえで、具体例から抽象化につなげる指導例を紹介します。

関数って、変数ってどういうものか？

なぜ関係を表す式を答えさせられるのか？

スモールステップでわかりやすく積み上げていく指導法を、示します。

では、どうぞ。

関数とは何か？

関数とは何か。

この点にかんしては２つの定義があります。

しかしどっちの定義を使うかは統一されていません。教科書や参考書によって、出版社によって、そしていつの時代の教科書かによって、まちまちです。こうした混乱のため、比例と反比例を習う中学１年生も、われわれ大人も、知らず知らずのうちに２つの定義を混同してしまっています。

 

また、関数という分野は、中１のはじめから習ってきた計算分野とは趣を異にする分野です。

それなのに、そのことを伝えないまま比例・反比例に入ってしまうと、中学生は何を求められているのかわからず「答えってこれでいいの？」と不安をおぼえてしまう。

 

こうした混乱と、見通しの悪さが、中学生をして「比例と反比例よくわからない」にしてしまう原因のひとつです。

そこでまずは、われわれ教える側が「関数とは何か」を正確に理解すること。

これが必要になります。

 

数学の４分野

さきに、関数という分野が数学のなかでどう位置づけられているのか、見通すところから始めましょう。

数学にはおおきく分けて「計算(代数)」「関数(解析)」「図形(幾何)」「統計(情報)」という４つの分野があります。

先に進むほど４分野はからみあい混じっていきますが、中学・高校で習う数学はとにかくこの４つに分けられます。

そして中学・高校で習う単元を４分野別に分けると、以下のとおりです。

 

ここで数学の歴史にかるく触れると、代数と幾何はともに歴史が古く、古代オリエントまで遡れます。

いっぽう関数（解析）が誕生したのは17世紀の西ヨーロッパ。

デカルトが座標平面を発案したことに始まり、ニュートンやライプニッツらによって解析学へと発展します。

この関数の登場によって、図形を代数的にあつかうことが可能になった。つまり砲弾が描く放物線軌道や、天体が描く楕円の面積、光の波長などを予測・分析できるようになったのです。これが近代科学の幕開けです。

（統計も同じく17世紀頃に登場し、19世紀以降の統計的自然観および保険業の発達によって発展）。

 

つまり関数とは、計算と図形とを統合する分野なんです。

上に挙げた表で、数Ⅲ単元をぜんぶ関数に入れていますが、これは数Ⅲではもう計算も図形もぜんぶ関数のなかに入っているという意味でこうしています。

これくらい、関数は重要な分野です。

 

…ということを、初めに生徒に伝えるといいでしょう。

ジュウゴはかならず伝えています。

数学には４つの分野があって、「比例と反比例」から関数分野なんだ。

高校の最後には計算も図形もぜんぶ関数に入っちゃうんだ。

だからしっかり学んでいこう。と。

生徒の興味・関心や能力にもよりますが、中１だからってなにも知らずにただ学べ、そんな態度はとりたくありません。

まずは数学の地図の全体像を見通せるようにしてあげてください。

 

関数の１つめの定義

関数の位置づけがわかったところで、じゃあつぎに関数とはいったい何か、という問題が出てきます。

現行の中学校教科書では、最初にみたように、こう定義されます。

つまり関数とは、ある変数に依存して決まる値。

ようするに \(y\) のことを指す、という定義です。

 

あれ？わたしの理解とちょっと違う…。

こう思った方も多いでしょう。

そうなんです、現行の教科書では関数とは「２変数の対応関係それ自体をいう」とは書いていないんです。

だから数学史でいえば、いま（2019年）の日本の中学教育はオーギュスタン・ルイ・コーシーによる定義を採用しているということになります。

 

関数の２つめの定義

いっぽう、レオンハルト・オイラーによる定義は以下のとおりです。

つまり関数とは、２変数の対応関係それ自体。

ようするに \(y=2x\) などの数式そのもの、という定義です。

参考書ではこちらの定義を採用しているものもありますし、関数とはこっちの意味で理解しているという人も多いでしょう。

 

そして現代数学は関数をどっちで定義しているかというと、オイラーのほうなんです。

厳密にいえば、オイラーの定義を集合論で捉えなおし、関数とは一種の写像であるとしています。（写像の考え方はたとえば数Ⅲ「合成関数」などで出てきます）

 

なぜ現在の中学教科書がコーシーの定義を採用しているのかはわかりません。

おそらく1970年代の「数学の現代化」に反発してゆとり教育が推進された、そのなごりでしょう。

1970年代には義務教育にも集合論が導入され、たとえば1974年の教科書における関数の定義は以下のとおりでした。

これが、現代化時代(1972-1981年)の中学数学教科書における関数概念の定義だ！

現代化時代は小学校から集合概念を学んでおり、関数の定義でも、集合という概念は、既習のものとして説明なしに、用いられている。

#掛算 #超算数 #数学 #数学教育 #現代化数学 #数学教育の現代化 #関数 #集合 pic.twitter.com/S5ygH78a3n

— kistenkasten723 (@flute23432) 2018年11月6日

 

しかし、当時の教師・保護者たちは集合論に拒否反応を示し、また落ちこぼれる生徒も多かったため、1980年代から日本の公教育は「ゆとり」に舵を切ってゆきました。

その後2000年代になって学力低下が叫ばれ、学習内容は一部増えましたが、関数の定義が現代数学に沿ったかたちで統一されることはありませんでした。

 

以上が「関数とは何か」についての俯瞰的視点、パースペクティブになります。

これをふまえて、実際の「関数の導入」指導に入っていきます。

 

…

…で、実際に指導方法を書いてみたら膨大な量になったので、記事を分けます。

次回、「関数の導入」指導例はこちらから↓

中学数学「比例と反比例」の教え方②　関数の導入と用語の説明

 

いちおうのまとめと補足

 

ここまでのまとめ

数学には「計算」「関数」「図形」「統計」という４分野があること。

なかでも関数は計算と図形とを統合する分野であり、17世紀以降の近代科学発展を支えてきた重要な分野であること。

 

関数の定義は２通りあり、

• 独立変数に依存して決まる値（従属変数）を指す
• ２変数の関係そのものを指す

このうち前者が現行の中学教科書で取り入れられていること。

しかし現代数学では、後者の定義を集合論で拡張した定義であること。

 

かつて日本でも後者の定義が教えられていたが、「数学の現代化」への反発から削除されたこと。

そしていまだ関数の定義は統一されていないこと。

 

こうした視野を、数学教育に携わる者は持っておくべきである。

以上がここまでのまとめです。

次の記事→中学数学「比例と反比例」の教え方②　関数の導入と用語の説明

[関連記事]

比例と反比例③ 比例の式を求める

比例と反比例④ 反比例の式を求める

比例と反比例⑤ 座標とグラフ

比例と反比例⑥ 文章問題のコツ(基本・応用)

比例と反比例⑦ 文章問題のコツ(図形・速さ・歯車)

 

補足：解析、統計的自然観、集合論

なお補足として、記事中ではさらっと流してしまった内容に触れておきます。

まず関数と解析のちがいについて。

記事では「関数(解析)」と一緒にしてしまいましたが、解析とは本来関数の発展版で、おもに極限や収束を扱う分野です。理系出身の人にとっては何をいまさらという話ですが、この極限・収束などの操作によってはじめて、ユークリッド幾何学で扱えなかったさまざまな図形が代数的に処理できるようになりました（曲線、波、回転etc.）。結果として解析学はあらゆる運動を数学的にとらえる強力な道具となり、またあらゆる設計の道具ともなって、今日の科学文明の土台となっています。

よって関数という分野の中心にどっかとすわる解析、という図式が成り立つわけです。

 

また「19世紀以降の統計的自然観」とは何か。

これは量子力学に代表される統計的手法があまりに有効なため、自然も人間もぜんぶ統計的に処理するんだ、処理するしかないんだ、そういう観方のことです。ようするに確率、平均、正規分布などで世界を理解しようという考え方で、決定論的自然観（ラプラスの悪魔や、アインシュタインの「神はサイコロをふらない」などの考え方）と対立する観点です。今日の実験科学、経済学、行動心理学その他あらゆるところにこの統計的自然観が顔を出し、われわれのものの見方さえ規定しています。

これに加えて、20世紀以降は保険業の発達がますます顕著なため、中学数学にも統計分野がすこしずつ入ってきているわけです。おそらく今後、指導要領の改訂のたびに、統計分野の単元はさらに増えていくでしょう。

 

最後に、集合論がなぜ数学の現代化で登場したのか。

これは現代数学の論文の大半が、集合論のことばで書かれているからです。なぜなら集合論は概念を定義するとき非常に便利だから（そもそも集合＝概念。「犬」の集合は「犬」という概念と同じこと）。たとえば20世紀初めの数学者ゴットロープ・フレーゲが数そのものを定義したときも集合論を使いました（どう定義したかは『フェルマーの最終定理』という本のなかで紹介されています）。概念というあやふやなものを厳密に定義できるため、とくに20世紀以降、数学界では集合論の考え方を使うのが常識になったのです。

この数学史の潮流に数学教育も乗り遅れるな、というのが、スプートニクショック後の資本主義世界での「数学の現代化」だったわけです。

 

 

補足は以上。

次回は「関数の導入と用語の説明」の指導方法を具体的に解説します。

>次の記事へ

 

その後は

• ３回目：比例でつまずくポイントの解説
• ４回目：反比例でつまずくポイントの解説
• ５回目：座標やグラフに入ったときの注意点
• ６回目：文章問題のコツ（基本・応用）
• ７回目：文章問題のコツ（図形・動点・速さ・圧力・歯車・てんびん）

という構成を予定しています。