中1数学「文字と式」の解説3回目。
今回は分数のまじった複雑な計算問題の指導について見ていきます。
つまり、
$$ \frac{2}{5} (10x-25) \quad \frac{4x+5}{3} \times 6 $$
とか、
$$ (9x-6) \div (-15) \quad \left( -\frac{1}{3}x – \frac{3}{4} \right) \div \frac{5}{12} $$
とか、
$$ \frac{3x-y}{4} – \frac{5x-7y}{6} $$
といった問題でつまずく生徒への対処法です。
[文字と式の記事一覧]
- 文字と式①:文字式計算の導入
- 文字と式②:途中式と分数、かっこ外し、分配法則
- 文字と式③:分数まじりの複雑な計算
- 文字と式④:数量の表し方
- 文字と式⑤:規則性の問題
文字式単元さいごの計算になります。
ここを乗り越えるか、「まぁ難問はできなくてもいいや」で済ませるか。
それによって、中3時に行ける高校が変わってきます。
つまり分数をふくむ複雑な計算もできるかどうかは、偏差値50以上の高校に進学できるかどうかの最初の分かれ目なのです。
大学進学を望むなら、ここはしっかりとできるようにしましょう。
スポンサーリンク
分数まじりの分配法則:かけ算
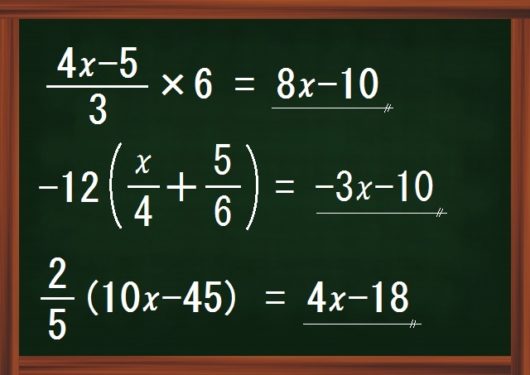
まず上図のような、分数まじりの分配法則の計算問題について。
ここでの指導目標は、図のように、「一発で正答できる」状態です。
「え?途中式を書かないの?」
はい。ここでは書かせません。
なぜならいつまでも途中式を書いていたら、余計に混乱するから。
そして次の「1次方程式」で困ることになるからです。
(数学指導法の記事一覧はまとめページへ)
原因
分数まじりの分配法則計算で、生徒がつまずく原因は主に3つです。
- 途中式を書くことで混乱している
- 分数のかけ算が暗算できない
- 単純に、練習不足
1.について。
論より証拠。学校準拠の教え方を見てもらいましょう↓
こうした丁寧なやり方は、最初の理解には有効です。
しかしずっとこうした途中式を書いていたら、式がややこしくなって、ミスの増加につながります。
とくに生真面目な生徒ほど、書かなくてもいい途中式をいつまでも書いて、まちがえる。
そんなことのないよう、ここでは一発で答えが出せるように導いてあげましょう。
![]()
2.について。
一発で答えを出すためには、分数のかけ算を暗算できる必要があります。
とりわけ(分数)×(整数)の約分を頭の中で処理しなければいけません。
よってたとえば、
$$ \frac{5}{6} \times 12 =10 $$
が瞬時に答えられない・暗算できない生徒には、まず(分数)×(整数)を復習すべきです。
![]()
3.については、そのままです。
速く正確に正答できるようになるまで、何度もくりかえし練習させましょう。
以下、1.2.3.すべてを解消するための指導案です。
指導案
①(分数)×(整数)問題の復習をする。
具体的にはまず、小6「分数のかけ算」のドリルなどを用意して、(分数)×(整数)の問題を示す。
$$ \frac{5}{6} \times 12 $$
ここで「約分の\を書かずに、暗算でやってみて」と伝える。
最初のうち、むずかしければ、約分後の数を頭の中に保持するよう指導する。
つまりこう。
先生「\(6\) と \(12\) で約分、上に何が残る?」
生徒「\(2\)」
先生「\(5 \times 2\) ?」
生徒「\(10\)」
$$ \frac{5}{6} \times 12 = 10 $$
これを自力でパッとできるまで、くりかえさせる。
②以下のような問題を示し、おなじく約分後の数を頭の中に保持するよう指導していく。
$$ \frac{4x-5}{3} \times 6 $$
先生「\(3\) と \(6\) で約分。上に何が残る?」
生徒「\(2\)」
先生「\(2\) を分配する。\(4x \times 2\) で?」
生徒「\(8x\)」
先生「\(-5 \times 2\) で?」
生徒「\(-10\)」
\begin{eqnarray} & &\frac{4x-5}{3} \times 6 \\&=& 8x-10 \end{eqnarray}
目の前で数問させた後、類題を練習させる。
③以下のような問題を示し、おなじく約分後の数を頭の中に保持するよう指導していく。
$$ -12 \times \left( \frac{x}{4} + \frac{5}{6} \right ) $$
先生「\(-12\) と \(4\) で約分。上に何が残る?」
生徒「\(3\)」
先生「符号つきで答えて」
生徒「あ、\(-3\)」
先生「\(-3 \times x\) で?」
生徒「\(-3x\)」
\begin{eqnarray} & &-12 \times \left( \frac{x}{4} + \frac{5}{6} \right ) \\&=& -3x \end{eqnarray}
先生「つぎ。\(-12\) と \(6\) で約分。どっちに何が残る?」
生徒「上に \(-2\)」
先生「そう。\(-2 \times +5\) で?」
生徒「\(-10\)」
\begin{eqnarray} & &-12 \times \left( \frac{x}{4} + \frac{5}{6} \right ) \\&=& -3x-10 \end{eqnarray}
目の前で数問させた後、類題を練習させる。
④以下のような問題を示し、おなじく約分後の数を頭の中に保持するよう指導していく。
$$ \frac{2}{5} (10x-45) $$
先生「\(5\) と \(10x\) で約分。どっちに何が残る?」
生徒「上に \(2x\)」
先生「\(2 \times 2x\) で?」
生徒「\(4x\)」
先生「つぎ。\(5\) と \(-45\) で約分。どっちに何が残る?」
生徒「上に \(-9\)」
先生「\(2 \times -9\) で?」
生徒「\(-18\)」
\begin{eqnarray} & &\frac{2}{5} (10x-45) \\&=& 4x-18 \end{eqnarray}
目の前で数問させた後、類題を練習させる。
注意点
目の前でさせたとき、つまったり、ミスしたりする生徒もいます。
そんな子には、前回の記事↓で指摘したように、「符号」→「数字」→「文字」の順でこまかくさせるといいでしょう。

また、②や④の計算でむずかしがる生徒には、約分後の数字を書かせてもいいでしょう。
つまり↓のように、です。
ただ③の計算では、書かせずに、必ず暗算させることが大切。
なぜなら分母がふたつあるので、約分後の数字がそれぞれちがうからです。
約分後の数を頭の中で保持し、それをかける。
基本的には、この暗算ができるようになることが、当単元で求められる力です。
できるまで、練習させてください。
ちなみに、なぜここでは途中式を書かせず、暗算できるようにすべきなのか?
それは、上でもちょっと書きましたが、次の「1次方程式」の以下のような問題で困らないようにするためです。
$$ \frac{2}{3}x – \frac{3}{4} = \frac{1}{2} x+ \frac{5}{6} $$
この方程式をかんたんに解くには、両辺に最小公倍数12をかけて、整数にします。
$$ 8x-9 = 6x+10 $$
このとき、頭の中で、以下の計算を暗算できないといけません。
$$ 12 \times \frac{2}{3}x \quad 12 \times -\frac{3}{4} \quad 12 \times \frac{1}{2}x \quad 12 \times \frac{5}{6} $$
約分を暗算でできない中学生は、ここでつまずくのです。
だから前もって、約分を暗算できる力をつけてあげるのです。
先々を見据えて、つまずきやすい石はあらかじめ取り除いてあげる。
「途中式を書かせるべきかどうか」は、つねにこのことを念頭において判断すべきと考えます。
[関連記事]
中1「1次方程式」④ 分数
分配法則:わり算
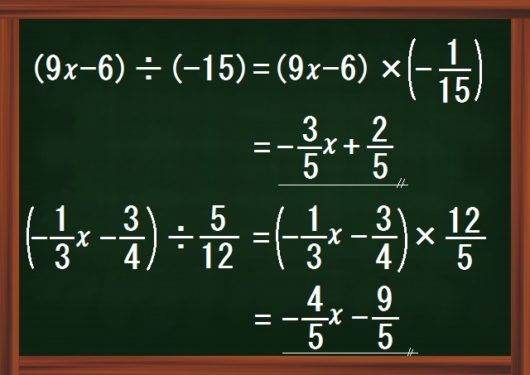
次に、「分数まじりの分配わり算」について。
先程の「分数まじりの分配かけ算」とちがい、ここでは、逆数にしてかける途中式を書かせる指導をおこないます。
ただそれができれば、ここは難しくない。
ここを難しいと感じるなら、それはいままでの単元の何かが抜けているということ。
つまり「分数まじりの分配わり算」問題は、いままで身につけるべき力をちゃんと身につけているか、そのチェックポイントになるのです。
![]()
原因と解決策
前単元までの何かの力が欠けている
ここでつまずく原因は、これです。
具体的に、どんな力が足りないとどのようなつまずきが起こるのか、見てみましょう。
1.「÷とは逆数をかけること」という発想が身についてない
\( (9x-6) \div 3 \) はできるけど、
\( (9x-6) \div 15 \) になると手が止まる。
こんな生徒をよくみかけます。
これは、「÷とは逆数をかけること」という発想がまだ身についていないためです。
わり算とはすべて逆数にしてかけることだと、徹底しましょう。
くわしくは正負の数:乗除の記事内「指導案:除法が混じるとまちがえる生徒に」を参照してください。

2.途中式を書く習慣がまだ身についてない
÷とは逆数をかけるんだと教えても、なお手が止まる。
そんな生徒は、いまだ途中式を書く習慣が身についていない可能性があります。
いままでも散々言ってきたことと思いますが、ここでも再度、途中式を書くことを徹底しましょう。
途中式を書かせる指導について、くわしくは、以下の過去記事などを参照してください。


3.分数のかけ算が暗算できない
かけ算にした途中式までは書ける。
しかし、その後の分配計算でミスしたり手が止まる。
これは、分数のかけ算が暗算でできないのが原因です。
解決策は、上で述べたように、約分後の数を頭の中で保持させる指導。
再度、当記事の最初を参照して、できるように導いてください。
分配わり算の計算でつまずく原因は、主に以上の3つです。
それぞれ、過去記事にすでに解決案を書いていますので、生徒の状況によって適宜復習させてください。
![]()
「分子に項2つ同士」の加減
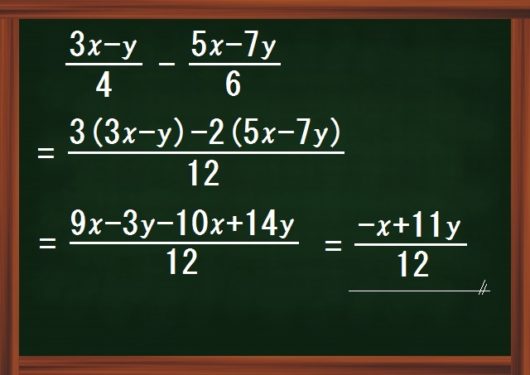
最後に、上図のような計算について。
こんな問題が「文字と式」単元最後の計算になります。
ここでつまずく場合もやはり、いままでの単元の何かが抜けているということ。
どこでつまずいたら、どんな力が足りないのか、具体的に示しますので、それぞれ復習させましょう。
原因と解決策
分子に項2つ同士の加減には、3段階の計算が必要です。
\begin{eqnarray} & &\frac{3x-y}{4}- \frac{5x-7y}{6} \\&=& \frac{3(3x-y)-2(5x-7y)}{12} \\&=& \frac{9x-3y-10x+14y}{12} \\&=& \frac{-x+11y}{12} \end{eqnarray}
どの段階でつまずくかによって、原因と解決策はちがってきます。
![]()
1.1行目から2行目でつまずく
最初の途中式が書けない。
こんな場合は、分数のたし算・ひき算ができないということです。
よって前回の記事内「分数計算ができない」を参照して、指導しましょう。

2.2行目から3行目でミスする
分子の分配法則の計算でまちがえる。
こんな場合は、分配法則の基本問題でつまずいています。
やはり前回の記事内の「分配法則でまちがえる」を参照してください。

3.3行目から4行目でミスする
最後、分子の同類項をまとめることができない。
こんな場合は、文字式の最初の計算に原因があります。
よって前々回の記事「最初の計算でつまずく」をまるごと参照し、復習させてあげてください。

4.4行目の約分でまちがえる
たとえば、以下のようなミスをする生徒をたまにみかけます。
\begin{eqnarray} &=& \frac{6x-5}{8} \\&=& \frac{3x-5}{4} \end{eqnarray}
つまり、片方だけと約分してしまうミスです。
こんな生徒には、3つぜんぶ揃わないと約分できないと伝えましょう。
そして実際にやってみせ、類題を数問させてみてください。
その後、約分できるのかできないのか、正しく判断できるようになったら、はじめて理由を伝えます。
$$ \frac{6x-5}{8} = \frac{6}{8}x -\frac{5}{8} $$
理由は上のとおりです。
だから3つ揃ってはじめて約分できるんだと、納得(=記憶を強化)させてあげてください。
以上の4つが、分子に項2つ同士の加減における、つまずく原因・解決策です。
すべて解決してあげれば、どの生徒もスラスラ正答していくでしょう。
まとめ

○\( \frac{4x+5}{3} \times 6 \) などでつまずく生徒に…
まず(分数)×(整数)の問題が暗算できるように復習する。
そして約分後の数を頭の中に保持することで、途中式を書かずともできるように導く。
難しがる生徒には「符号」→「数字」→「文字」の順でこまかく計算させる。また、約分後の数をちいさく書かせてもよい。
*途中式をいつまでも書いていたら、次の「1次方程式」でつまずくから。
○\( (9x-6) \div (-15) \) などでつまずく生徒に…
前単元までの何かの力が欠けていることが原因。該当箇所を復習する。
「÷とは逆数をかけること」という発想が欠けている
→正負の数:乗除
途中式を書く習慣が欠けている
→小5の分数、かっこ外し、四則混合
分数のかけ算が暗算できない
→当記事の最初
○\( \frac{3x-y}{4}- \frac{5x-7y}{6} \) などでつまずく生徒に…
前単元までの何かの力が欠けていることが原因。該当箇所を復習する。
分数のたし算・ひき算ができない
→小5の分数
分配法則の基本問題でまちがえる
→分配法則
同類項をまとめるところでミスする
→文字式最初の計算
約分ミス
→3つ揃わないとできないと教え、習熟した後、理由も伝える。
次回は「文字を使った数量関係の表し方」を解説します。




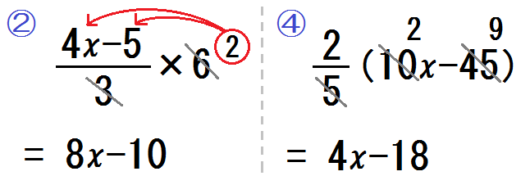
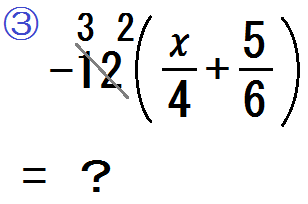



コメント
立て続けに失礼します。
文字式の計算をはじめに習ったときはいませんが、
数か月後、一次方程式を習ったあとにやると、
(x/2)+(x/3)
=3x+2x
=5x
と計算してしまう生徒が少なくありません。
その都度、
「分母を払っていいのは、方程式(等式)のときだけ、
きみがやっているのは、
(1/2)+(1/3)
=3+2
=5
と同じだ」
などと注意しますが、なかなか直りません。
このようなミス(悪癖)を防ぐ良い方法があれば、ご教示ください。
ご指摘のようなミス、多くありますね。
防ぐ方法として、私がよくやるのは、「毎年こんなミスをする中学生が多いんだよー」と言ってあらかじめご記載のようなミスを示すことです。
そのうえで、「次の式を計算しなさい」なのか「次の方程式を解きなさい」なのか、問題をよく読めと伝えます。
それでもやはり、言ったとおりのミスをする子は毎年います。
そんな子には「次の式を計算しなさいって問題だろ」と指摘すると、「あー」と納得してくれます。
あらかじめよくやるミスを伝える、というのがいいみたいですね。
伝えておかないと、その場で指摘しても、後出しジャンケンされたような不満げな表情になりますからね。
ちなみに、計算と方程式の違いを説明しだすとドツボにはまるので、あまりおすすめしません。
アドバイスありがとうございます。
確かに、よくあるミスを先に伝えておく、というのは良さそうですね。
今度試してみたいと思います。
{(4x-5)/3}*6の問題ですが、
指導案では、途中式はなしですが、
やはり、初期の段階では、途中式を書かせた方が良い気がしますが、いかがでしょうか。
2を分配することを忘れ、
与式=4x-10のような計算ミスをしてしまわないでしょうか?
ご指摘のような計算ミスはほとんど見受けません。
それよりも、初期の段階で途中式を書くことで、暗算力が身につかないことのほうが怖い。
1次方程式の分数問題が解けなくなるからです。
不安な生徒には、記事にあるように、約分後の数字を書かせればのりこえられると思います。
ご回答ありがとうございます。
確かに、暗算力を身につける、という意味では、
途中式は書かない方がいいですね。
ただ、分母を払った後は分配法則を使う、ということをまずは理解させる必要があると思います。
その意味で、途中式を書かせた方がよい、と考えています。
もちろん、それを理解した後は、途中式は不要ですし、
分配法則を使うことを、はじめから理解できる生徒であれば、
はじめから途中式は不要でしょう。
中1数学 文字と式③
×「1方程式」
〇「1次方程式」
素晴らしいブログですね。中3まで完成させてほしいです(笑)
ありがとうございます。中3まで完成させたいとは思っています。
「1方程式」まちがってましたね、修正しますm(_ _)m