「中学から、数学がわからなくなった…」。
こんな生徒と対峙したとき、どう指導すべきか?
悩んでいる人も多いと思います。
私も過去13年間おなじ悩みをもち、諸先輩方に教わりながら、試行錯誤をくりかえしてきました。
そこでその経験と蓄積を活かし、「こんな教え方もあるよ」というノウハウを提供させてもらいます。
いわゆる「勉強のしかた」ではなく、「この単元でつまずいている場合、どのように教えたらいちばん理解が早いのか」という具体的な指導法を書いていきます。
いま、中学生をもつ保護者の方。
塾講師や家庭教師をしている方。
指導に悩む中学校数学教員の方。
参考になればさいわいです。
なお、子どもが中学数学でつまづく原因は主に3つです。
- 練習不足(速く・正確に解く練習がたりてない)
- もっと前の単元でつまずいている(小5の分数など)
- 理解があやふや
このうち1.と2.に関しては、よく言われるように、ドリルなどをつかった反復練習が有効です。
どの単元から復習すればいいかはそのつど指摘しますが、このブログでのメインは3.の解決法になります。あしからず。
(数学指導法の記事一覧はまとめページへ)
1回目は中1「正負の数」の加減とかっこ外しについて。
とくに以下のようなまちがいをする生徒、
\begin{eqnarray} -7+4 &=& -11 \\ -7-4 &=& -3 \\ -6+(-2) &=& -4 \\ -6-(-2) &=& -8 \end{eqnarray}
つまり正の数・負の数の最初の計算でまちがえてしまう。
また、かっこ外しの際にまちがえてしまう。
これら2点の場合において、原因、解決法、注意点をそれぞれ解説します。
スポンサーリンク
加減の最初の計算でまちがえる
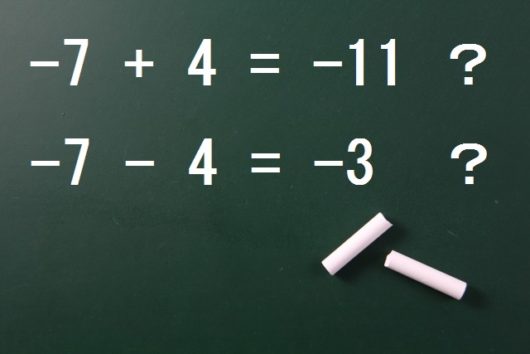
中学1年生になって最初の数学単元である「正の数、負の数」。
その最初の計算問題で、図のようなまちがいをしてしまう生徒をたまにみかけます。
このようなつまづきは、「+」「-」が符号であることを徹底させると解決します。
[関連記事]
原因
たとえば\( -7 -4 = -3 \) としてしまう生徒の場合、頭の中でこんな処理がおこなわれています。
つまりこのような生徒は、「-」というマークが計算記号なのか、数字の前につける符号なのか、ごっちゃになっている状態なんです。
こうなってしまう原因の一端は、現行の公教育にもあります。
教科書をみても、ある箇所では「-」をひき算の意味で使っていたり、またある箇所では「マイナスという符号」の意味で使っていたり。ばらばらです。
そこで、このような中学1年生には、「+」「-」とは数字の前につく符号であると統一させると、スムーズにいくことが多々あります。
![]()
指導案
①まず「+」「-」を「プラス」「マイナス」と読ませる。
生徒が「たす」「ひく」と読んだら、そのたびに訂正する。
そして「+」「-」とはぜんぶ、数字についている符号だと教える。
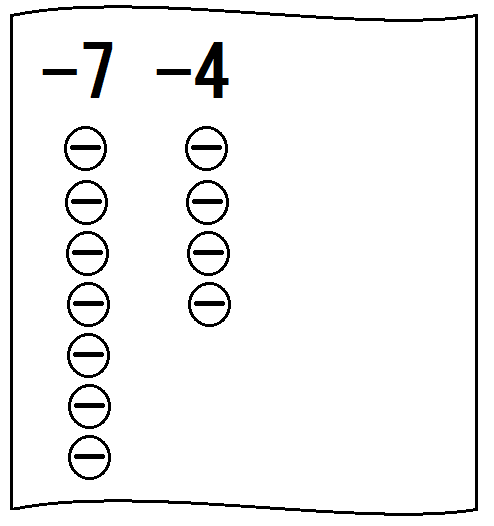
②「-7 -4」は「-7と-4の計算」だと言う。
そしてこんな図を書く↓
「マイナスはぜんぶで何個ある?」と聞く。
生徒が「11(コ)」と答えたら、「そう、答えはマイナスが11、つまり-11」と言って、「-11」と書く。
③「-7 +4」は「-7と+4の計算」だと言う。
そしてこんな図を書く↓
「+と-は打ち消しあう」と言って、取り消し線をひく。
そして「どっちが何個残った?」と聞く。
生徒が「マイナスが3(コ)」と答えたら、「そう、答えはマイナスが3、つまり-3」と言って、「-3」と書く。
④同様の練習問題を一緒に解く。
生徒が計算に慣れてきたら、自分でさせる。
注意点
「+」「-」は符号、と徹底させることがコツ。
ジュウゴはここでつまずく生徒に、「この世に足し算、引き算なんてない!ただ符号のついた数を計算するだけだ!」と指導しています。
また最初で+を「プラス」、-を「マイナス」と読ませることも重要。
中2、中3になっても基本計算でまちがえる生徒ほど、「たす」「ひく」と言いつづけています。
中1の早い段階で、算数ではなく数学に切り替わったと体感させましょう。
なお、「整数問題はできるけど、小数・分数計算になるとわからない」という場合は、小学校時ですでにつまずいている可能性が大です。
小4または小5の小数・分数計算問題を解かせてみて、様子を観察してください。
観察ポイントは4つ。
- 小数点の位置などの基本ルールが身についているか?
- 2桁+2桁、2桁×1桁くらいは横算のまま暗算できるか?
- 異分母のたし算・ひき算の際に途中式を正しく書けているか?
- 最小公倍数、最大公約数はノータイムで導き出せているか?
以上の4つのうち、ひとつでも欠けていたら、それはつまずきです。
(最小公倍数と最大公約数のコツについてはこちらも参照→中学数学「文字と式」②注意点)
4つすべて揃うまでその単元を算数ドリルなどで反復練習させましょう。
なぜこの教え方か?
一般的に「正負の数の加減」では、数直線をつかって導入する場合がほとんどです。
教科書でも、あまたの参考書でも、そして多くの教育ブログでも、数直線をつかって説明しています。
しかしジュウゴはこれに反対です。
理由は2つ。
- 数直線より個数のほうが子どものイメージに訴えやすいから。
- 数直線による説明では「+」「-」を計算記号ととらえてしまうから。
そもそも数直線という概念(つまり直線上の位置を数と考える方法)は、17~18世紀のヨーロッパでやっと成立したものです。
これは砲弾の軌道や天体の運行といった、連続量および位置関係を数学的に扱う必要が生じたからです。
数には
- 個数(1個、2匹、3人…)
- 順序(1番、第2、3日目…)
- 連続量(長さ、面積、質量…)
- 位置関係(ベクトル、時点…)
という4つの性質があって、下にいくほど歴史も新しく、理解も難しくなります。
だから、連続量と位置関係という2つの概念をふくんだ数直線で、正負の数の加減を教えることは、子どもにムダな負担を強いているのです。
よって私はすでに述べたように、+・-の○を書いて、個数で指導しています。
余計なところで、子どもの頭を悩ませないようにしましょう。
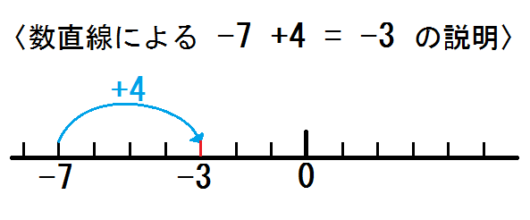
また、数直線で上図のように説明してしまうと、「-7に4をたす」と理解してしまいます。
子どもが計算記号と符号とをごっちゃにしてしまう原因、\( -7 +4 = -11 \) とまちがえてしまう原因も、実はここにあるのです。
「+」「-」は計算記号じゃなくて、符号。
これを徹底するためにも、数直線でなく、個数でイメージさせて指導するとよいでしょう。
とくにつまずいている生徒ほど、です。
かっこ外しでまちがえる
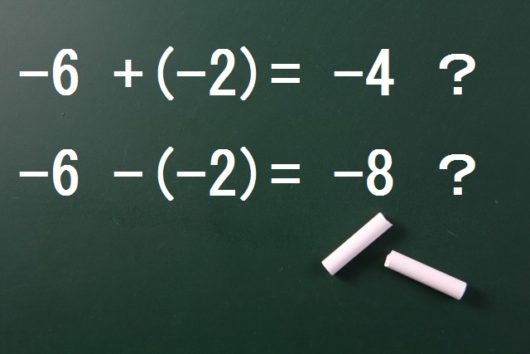
つづいて「正負の数の加減」におけるかっこ外しについて解説します。
かっこを外す計算でも、まちがえる中学生を散見します。
このようなつまづきは、教え方と教える順序を整理整頓することで、ほとんどの場合解決していきます。
[関連記事]
原因
正負の数の加減におけるかっこ外しでまちがえる原因は、主に3つです。
- かっこ外しのルールが正しく身についていない
- 途中式を書かずにやろうとしている
- かっこは正しく外せるけど、その後の計算でまちがえる
このうち1.の原因の場合が非常に多い。
というのも、学校での教え方と教える順序が、以下のように入り組んでいて複雑だからです。
↓
↓
↓
Ⅲ.まで丁寧に学習したあと、急にⅣ.のかっこ外しを習うんです。
かなりの生徒が「え、じゃあ今までのは何だったの?」となります。
なかには混乱して、かっこをどのように外したらいいのか迷ったままの生徒が出るのもムリありません。
ではどうすればいいのか?
指導案
①まず上の章で解説したように、かっこのない式で基本計算を学ばせる。
計算に習熟してくれば、Ⅰ,Ⅱのルールはおのずと身に付く。
「+どうし、-どうしの計算は、数字が増えるな」、
「+と-の計算は、頭の中でひき算だな」と。
気づかない生徒には、↑の声かけをして気づかせる。
これで「かっこは正しく外せるけど、その後の計算でまちがえる」という原因は解消される。
②下図のようなかっこのついた式を示し、「かっこのついた式はかっこを外してから計算する」と言う。
そして、下のような「かっこ外しのルール」を書いて示す。
ちなみに、学校で習うⅢのルールは計算上必要ない。
③下図のように波線をひき、ひとつ下に=を書く。
そして「+と-だから、どっちになる?」と聞く。
生徒が「マイナス」と答えたら、「そう、-2」と言って、書く。
このとき、「-6」はそのまま書くことを強調する。
これで「途中式を書かずにやろうとしている」という原因の対処にもなる。
最後に下に=を書き、「計算して」と言って、させる。
④別の問題を示して、今度は生徒にやらせてみる。
生徒の状況に応じて、声かけをする。
「-と-だから、どっちになる?」とか。
「-4を忘れるな。変わらないものもそのまま書くこと」とか。
⑤前にかっこのつく式も示して、「いちばん前のかっこは、そのまま外すだけ。関係ない」と言う。
そしてまた、生徒にやらせてみる。
⑥同様の練習問題を一緒に解く。
生徒が計算に慣れてきたら、自分でさせる。
注意点
むずかしい数学用語をできるだけ使わないこと。
聞きなれない言葉を使うと、そのたび生徒の思考はストップします。
たとえば①の段階で「同符号どうしの計算は絶対値の和に共通の符号を…」などと、教科書に準拠しようとして、いたずらに数学用語を使う必要はありません。
わかりやすい日常の言葉で伝えるように心がけましょう。
ちなみにジュウゴは、②の段階でかっこ外しのルールを示すとき、「同符号なら+、異符号なら-になる」とも言いません。
ルールを書いて、示すだけです。
このわけは下で解説します。
また、教える順序も指導要領に準拠する必要はありません。
とくに私教育の場合、その子にとって、そのクラスにとって、いちばん理解しやすい教え方・順序でいくべきです。
ジュウゴは1000人以上の中学生に対応してきた経験上、いまは上記の方法がもっとも良いと確信してるわけです。
つまり、「まずかっこのない計算に習熟させる」→「かっこ外しのルールを伝える」→「途中式を用いて正しい手順を理解させる」→「練習させて習熟させる」という教え方・順序です。
各々がいちばん良いと思うやり方でする。
私教育の長所はこの自由性にあるのだから、子どもより文部科学省の指示を大切にするような姿勢は省みるべきでしょう。
また、そもそもなぜ、かっこ外しのルールが上記のようになるのか?
生徒に質問された場合にそなえて、指導者があらかじめ知っておくことも大切です。
理由は、乗法から来ています↓
かっこ外しのすぐあと、「正負の数の乗除」で、-を偶数個かけたら+、-を奇数個かけたら-、と習います。
また次の単元である「文字と式」で、1およびかけ算記号は省略する、と習います。
よって、文字と式まで既習の生徒には、かっこ外しのルールのわけを教えてもいいでしょう。
![]()
なぜこの教え方か?
さきほど、かっこ外しのルールを伝える際に「同符号なら+、異符号なら-になる」とは言わないと述べました。
これは、いま見たように、かっこ外しのルールが乗法から来ているからです。
つまり、正しく伝えるなら、「マイナスが偶数個(0を含む)かけてあれば+、マイナスが奇数個かけてあれば-になる」なんです。
このちがい、微妙なようですが、後々おおきく響いてきます。
どこでかというと、四則混合です。
下の2つの計算を比較してください。
下の方法のほうが、途中式がひとつ少なく、計算も速くなります。
そしてこの計算速度のちがいは、学年が上がるほど顕著になっていきます。
たとえば中学2年生の最初、「式の計算」単元のこんな問題↓
\begin{eqnarray} -\left( -5xy \right)^2 \times \left( -6y \right)^2 \end{eqnarray}
この式を「すべてかけ算でつながってる」と捉えられたら、符号は一発で決まります。
マイナスが全部で5つだから、答えの符号は-なんです。
つまり、
\begin{eqnarray} &=& – \left( 25x^2y^2 \times 36y^2 \right) \\ &=& -900x^2y^4 \end{eqnarray}
このように、先々のことを考えて、「便宜上であってもまちがったやり方は伝えない、教えない」という姿勢が大事だと、ジュウゴは考えます。
かっこ外しのルールとして、「同符号なら+、異符号なら-になる」などとは伝えない。
それよりも、ただ例を示し、生徒自身にルールを体得させる。
もし言葉で伝えるなら、乗法のルールから来ていると正しい知識を伝える。
ただしこれは生徒が「文字と式」まで学習済みである場合に、です。
[関連記事]
まとめ

「正の数・負の数の加減」でつまずいている生徒に、どう指導したらいいか、具体的な教え方をみてきました。
まとめると、以下の教え方・順序で指導するといいでしょう。
1.「+」「-」は符号であると徹底する。
2.かっこのついてない式で、個数のイメージにより、加減の基本計算を導入する。
3.かっこのついてない式で、加減の基本計算を練習させる。
*整数問題はできるが小数・分数計算になるとできない場合は、つまずきポイントを見極めて、そこを反復練習させる。
4.かっこのある式で、かっこ外しのルールを提示し、同時に途中式を書くことを徹底しながら、計算方法を理解させる。
5.かっこのある式を練習させる。
6.「文字と式」まで学習済みの生徒には、かっこ外しのルールが乗法から来ていることを理解させる。そして、このルールの下に四則混合を解かせ、練習させる。
*なお、「文字と式」をまだ学習していない生徒に、正負の数の四則混合をどう教えたらいいかは、3回目の記事でくわしく解説しています。
この記事は管理人のジュウゴが、過去13年間の経験といろんな書籍情報をもとに書いています。
今後のさらなる経験や情報によって、改訂されていく余地アリです。
よって教育に携わる方からのご意見・ご感想は大歓迎です。
下のコメント欄から、随時おまちしています。
次回は「正負の数」の2回目、乗除と累乗の教え方を解説します。



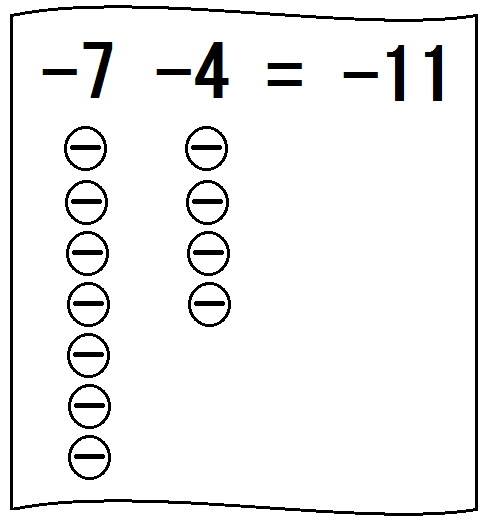

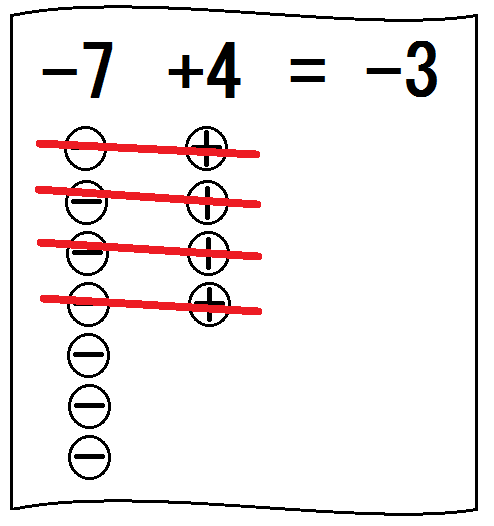




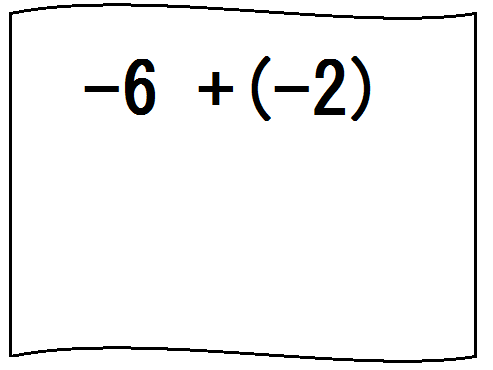
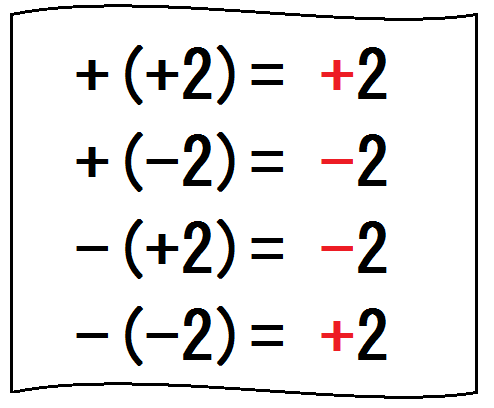
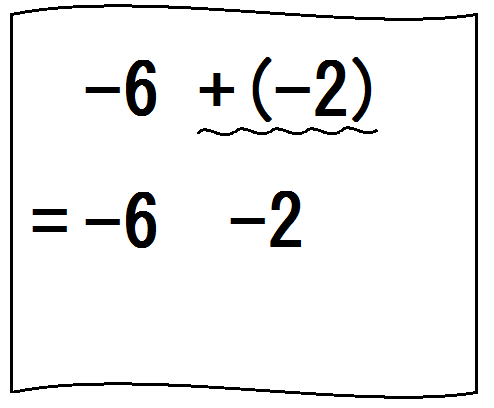
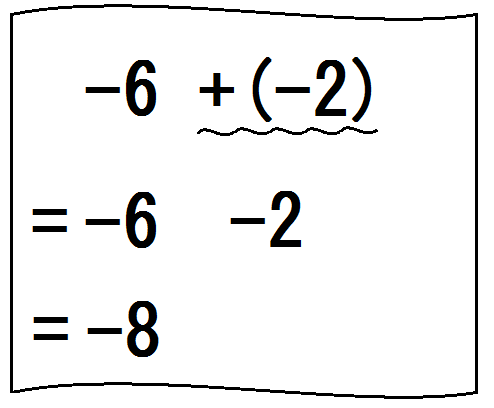
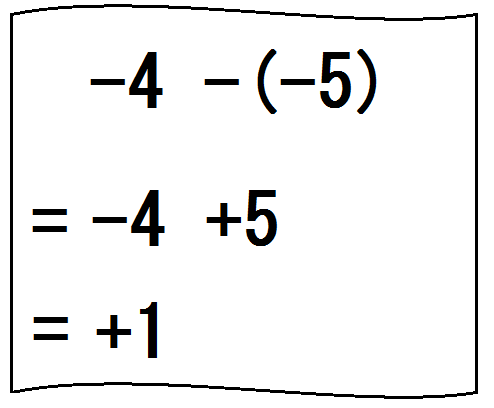
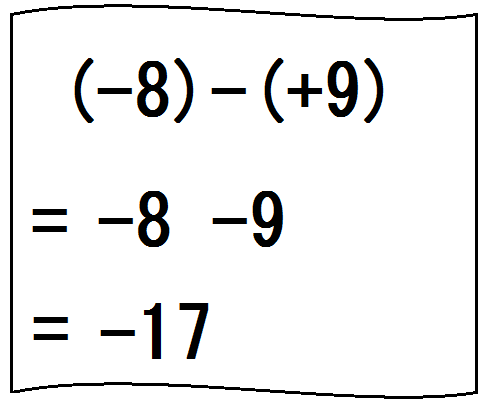



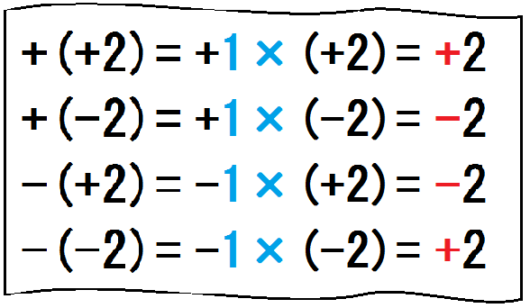



コメント
初めまして。中学数学を教えています。
この記事に出会って、目から鱗でした。教科書の「負の数の減法」の説明は、私が読んでいても「わかりにくいなぁ」とずっと思っており、これでは生徒たちは絶対に辛いだろうなと思いながら試行錯誤をしてきました。今回の記事を読み、さっそく試したところ、ほとんどの生徒がすらすらと解けるようになっていて、本当に良かったと思っています。
一つ。
例えば、-(-4)のかっこの外し方ですが、-1×(-4)の意味であることを説明し、「マイナスの数が何個かけられているか」という質問に対し「5個」と答える生徒は数名ですがおりました。「-4-7は、-が4個と-が7個で全部で11個だね」という説明と混同したように見受けられました。「足す・引く」という言葉を使わないようにしていたのですが、「-4」が-1が4個であって、マイナスの数が4個でないという説明に少し苦慮しました。
この点で、何かアドバイスが頂けたらと思い、コメントを書かせていただきました。
お忙しいところ恐縮ですが、よろしくお願いいたします。
返信が遅くなり申し訳ありません。
コメントありがとうございます。当記事がすこしでもお役に立てたなら幸いです。
-(-4)等のかっこの外し方に関しまして。
記事にもありますように、わたしはかっこ外しの最初、ルールだけを提示し、なぜそうなのかの説明はしません。
それで生徒が正しくかっこを外せるようになり、かつ正負の数の乗除(あるいは次章の「文字と式」)まで学んだ段階で、じつはあのルールは乗法から来てるんだとネタ明かしをします。
このような指導順ですと、質問者様の言われるような混同は、少なくとも今までは一回も起きませんでした。
ご参考になれば幸いです。
じゅうご先生
ありがとうございます!
家庭教師先の子、納得したみたいで、スラスラ解けていました……!
感動……!!!
50過ぎのおっさんですがご説明、腑に落ちました!子供への教え方含めてここしばらく悶々としてました。ありがとうございます!他の記事も読ませていただきます。
4月から小6になる子がいますが
驚きました!
わかりやすい!
たしかにそこの説明!
出来ないし、子供や私までも
思い出すとつまづいていたし
つまづきそうだし。。。
助かる!
と思いました。
いや、本当
わかりやす過ぎです
(o^^o)
このブログにいきついて
感謝です。
これからも拝見致しますー♪♪♪
(すみません、さきほど途中で送信してしまったので、再送いたします)
>指導案②「-7 -4」は「-7と-4の計算」だと言う。
についてですが、
生徒さんが、「-7とー4の『計算』って何?」とならないでしょうか?
やっていることは、「-7(マイナスが7個)」と「-4(マイナスが4個)」の足し算ですよね?
であれば、「-7とー4の『足し算』」と説明した方が良くないでしょうか?
>「この世に足し算、引き算なんてない!ただ符号のついた数を計算するだけだ!」
も少々言い過ぎな気がいたします。
中学数学でも、例を挙げるまでもなく、足し算、引き算、たくさん出てきますよね?
やはり、(-7)+(-4)=-11、
をー7とー4の足し算として説明した後、
+()が省略されたパターンを、
-7-4
=(-7)+(-4) ←慣れてきたら省略
=-11
のように、+()が省略されているだけで、同じくー7とー4の足し算なんだ、
と説明するのが良いかと思いますが、いかがでしょうか。
ご意見いただければ幸いです。
よろしくお願いします。
ご意見ありがとうございます。
サンダー様の言われる指導方法と、ブログに書いた指導方法、両方をジュウゴは試してきました。
結果、後者のほうが圧倒的に「つまずいている子」には効果的だったので、そのように主張している次第です。
指導事例数としては数百人程度です。
サンダー様の方法で指導した場合、演習段階で「-7+4=-11」というミスが多発しました。
「そうじゃない、-7と+4の足し算で…」などと注意していくと、中1最初でつまずく子ですから、よけいに混乱していくことが多かったのです。
よって、+-は符号という意識を植え付けるために、この指導方法にいま落ち着いています。
最初に○で導入すれば、「-7と-4の『計算』って何?」となる子は、いまのところ一人もいません。
ただ、「計算があるだけだ」はご指摘のとおり言い過ぎです。
極論を言って、要点をつかませて、その子ができるようになってから、のちのち訂正しています。それ、書いてませんでした、ごめんなさい。
早速ご回答いただき、ありがとうございます。
なるほど、「-7+4=-11」の例で納得です。
「足し算」という言葉を使うと、「足し」との言葉に引きずられ、
数字のみ、つまり、「7」と「4」を「足し」てしまう、
ということですね。
「計算」の意味についても、○+や○-を使って説明すれば、混乱はない、ということですね。
ただ、やはり、「計算」というと、なんだか漠然としている気がするので、
もう少し具体的な、「+とー、どっちが多いかの計算」とか言った方がいい気もします(単に「計算」の方が、簡潔でいいのかもしれませんが)
私も、教科書に載っている方法(上記のⅠ~Ⅳの方法)は、分析的ではあるけれど、わかりにくいと感じていました。
ですので、今後は、こちらの方法を試してみたいと思います。
そこで、もう1点教えていただきたいのですが、
こちらの方法は、教科書に載っている方法とは違う、という点で、
生徒さんが戸惑った、ということはなかったでしょうか?
もしあれば、どのように対処されたか、教えていただけないでしょうか?
よろしくお願いします。
>こちらの方法は、教科書に載っている方法とは違う、という点で、
>生徒さんが戸惑った、ということはなかったでしょうか?
記憶するかぎりでは、一度もありません。
子供は、最終的な理解にたどりつきさえすればその道筋は何でもいいという教育の自由性を、大人のわれわれより見抜いているように思います。
教科書の教え方、学校でこう言われた、指導要領・・・、権威に弱いのはむしろ大人のほうみたいです。
子供の伸びやかな思考に接するたび、自戒させられます。
ご回答ありがとうございました。
確かに、大人の方が気にしすぎているのかもしれませんね。
これからも、ちょくちょく質問させていただくと思いますが、
ご迷惑でなければ、回答いただければうれしいです。
よろしくお願いします。
こちらこそ、ご意見ご感想いただけるのはうれしいのです、ありがとうございます。
>指導案②「-7 -4」は「-7と-4の計算」だと言う。
についてですが、
生徒さんが「『計算』って何?」、とならないでしょうか?
やっていることは、「-7(マイナスが7個)」と「-4(マイナスが4個)」の「足し算」ですよね?
であれば、「-7と-4の『足し算』」と言った方が、良くないでしょうか?
>「この世に足し算、引き算なんてない!ただ符号のついた数を計算するだけだ!」
というのも、少々言い過ぎな気がいたします。
中学数学でも、例を挙げるまでもなく、足し算、引き算、出てきますよね?
やはり、(-7)+(-4)=-11、
をー7とー4の足し算として説明した後、
+()が省略されたパターンでも、
-7-4
=(-7)+(-4)←慣れてきたら省略
=-11、
のように、-7とー4の足し算として説明するのがよいかと思いますが、
いかがでしょうか?
ご意見お聞かせいただければ幸いです。
35才の大人です。すっごく分かりやすいです!!中学生の時に、この教え方に出会いたかったです(笑)
転職の際の入社試験でマイナスとプラスの計算がでました。全く解けなかったので、こちらのサイトで勉強させていただきました。本当に助かりました!
ありがとうございます。大人の学び直しにもお役にたてたなら嬉しいかぎりです。遅々とした更新の個人ブログですが中学・高校数学の教え方、完成めざして書きつづけていきます。よければ他テーマの連載も覗いてやってください。