こんにちは、ジュウゴです。
数学って「それを学んでいったい何の役に立つんだ?」と思いますよね。
今回はそんな単元の代表格、高校数学の「三角比」について見ていきます。
三角比とは何か?
サイン、コサイン、タンジェントがいったい何の役に立つのか?
だれしも一度は思ったことがあるでしょう。
昔からそうだったみたいで、明治の俳人・歌人である正岡子規も「酒」という随筆の冒頭でこう書いています。
一つ橋外の学校の寄宿舎に居る時に、明日は三角術の試験だというので、ノートを広げてサイン、アルファ、タン、スィータ、サイン、アルファ、タン、スィータと読んで居るけれど少しも分らぬ。困って居ると友達が酒飲みに行かんかというから、すぐにいっしょに飛び出した。
(正岡子規「酒」筑摩書房p51より)

「春や昔」サイト様
正岡子規でも投げ出した三角比に、ド文系のジュウゴが無謀にもいどみます。
できるだけわかりやすく、その成り立ちから応用まで解説してみたいと思います。
三角比とは何か。その歴史と成り立ち
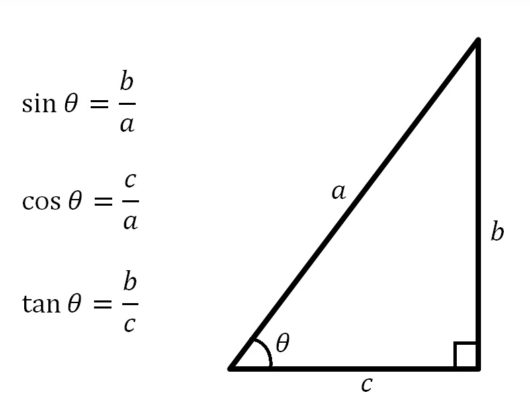
三角比の授業では、いちばんはじめに上の図のような定義を習います。
つまり直角三角形の3辺の長さをそれぞれ \(a\)、\(b\)、\(c\)として、左下の角度をθ(シータと読みます)とすると、
sin(サイン)θとは\( \frac{b}{a} \)を計算した値、
cos(コサイン)θとは\( \frac{c}{a} \)を計算した値、
tan(タンジェント)θとは\( \frac{b}{c} \)を計算した値ということにすると。
これいったい、いつ、だれが、なんのために考え出したんでしょうか?
三角比は測量のために生まれた
先に結論をいうと、三角比は紀元前2世紀に、アレクサンドリアの学者ヒッパルコスが考えだしたものです。
より正確にいうと、古代メソポタミアやエジプトからずっと考えられていて、ヒッパルコスによっていちおうの完成をみたのが三角比という分野です。
そして三角比はなんのために考え出されたかというと、測量のためです。
つまり長さや距離を測るために、生み出された考え方なんです。
長さや距離といっても、身長とかあそこの木までの距離とか、そんな小さなスケールじゃありません。それだったら巻尺つかえばいいし。
三角比を使えば、遠くの山の高さを測れたり、あるいは山や岬や島までの距離がわかって地図を描けたりするんです。
さらにヒッパルコスは三角比を使って、地球の半径や、地球から月までの距離も測っちゃったんです。
いったいどうやって測ったのか?
その方法をくわしく見ていきましょう。
サイン、コサイン、タンジェントの成り立ち
はじめに遠回りしますが、すこしだけ付き合ってください。
なぜって、ヒッパルコスの測量方法を理解するには、まずサイン、コサイン、タンジェントの意味を知る必要があるからです。
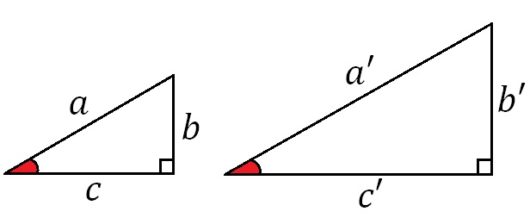
では突然ですが、中学3年生で習った「2つの角が等しい三角形は相似である」という定理を思い出してください。
相似とは、大きさはちがうけど形は同じということでしたね。
そして直角三角形の場合は、直角部分の角が等しいから、あと1つどこか角が等しければその直角三角形どうしは相似になります。
上の図でいうと、赤い角の部分だけ等しければ、2つの直角三角形は相似です。

つぎに、「相似な図形の辺の比は等しい」という定理も思い出してください。
上の図でいうと、\( a:a’=b:b’ \) だし、\(a:b=a’:b’ \) です。
後の式を分数で表すと、$$\frac{b}{a}=\frac{b’}{a’}$$となります。
(比を分数で表してもいいというのは、小学校で習いましたね)。
以上の2つから、1つの角度(上図の赤い部分)が等しい直角三角形であれば、どんなに小さくても、どんなに大きくても、\(a:b \) の比、つまり \( \frac{b}{a} \) の値は同じということがわかります。
つまり直角三角形では、1つの角度が決まると、自動的に \( \frac{b}{a} \) の値も1つに決まるんです。大きさ関係なしに。
それでヒッパルコスは、この \( \frac{b}{a} \) の値に特別な名前をつけたんです、「サイン」と。
おなじように \( \frac{c}{a} \) の値には「コサイン」、\( \frac{b}{c} \) には「タンジェント」と名付けました。
「三角比の表」を最初につくったヒッパルコス
それからヒッパルコスは、sin1°は0.0175、sin2°は0.0349、sin3°は0.0523…と、実際に値を出していきました。
赤い部分が1°の直角三角形を作って、\( a \)の長さと\( b\)の長さを測って、わり算すれば出ますもんね。直角三角形の大きさはなんでもいいですし。
(本当の求め方はちょっとちがうんですが、話が複雑になるので触れません。ついでに「サイン」「コサイン」「タンジェント」という名称も、本当はヒッパルコスが使っていた言葉ではないんですが、ややこしくなるので割愛します)。
コサインとタンジェントの値も同じように、ヒッパルコスは求めていきました。
こうして求めた値をぜんぶまとめると、下の表のようになります。
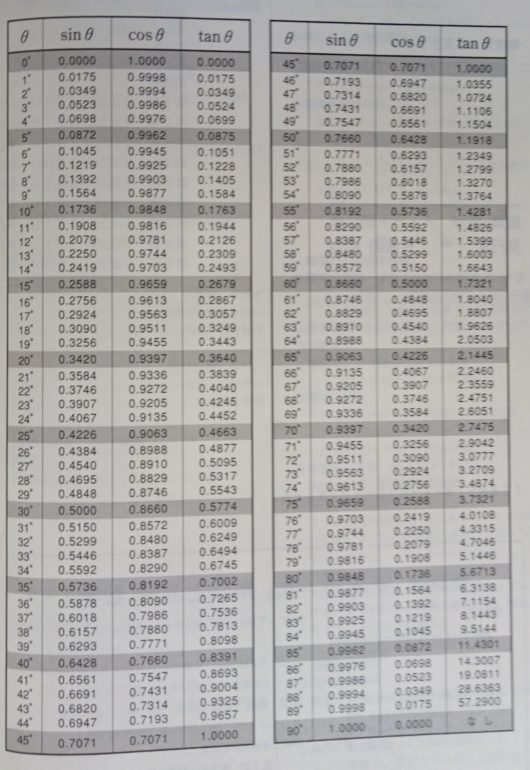
三角比の表
(数研出版「チャート式Ⅰ+A」巻末より)
そう、教科書や参考書にかならず載っている「三角比の表」です。
この表を最初につくったのがヒッパルコスだったんですね。
彼はこの値を使って、山の高さや、地球の半径や、月までの距離など、いろんな長さを測っていきました。
どうやったのか?もうちょっとでたどり着きます。
三角比をつかって山の高さを測る
まず、山の高さの測り方です。
下の図でいうと\(h\) の値を求めることになります。
山の高さを測るのに、頂上から真下にトンネルをほってメジャーを垂らすわけにはいきません。
そこで三角比の出番になります。
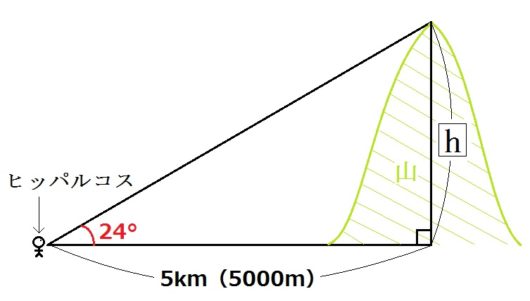
まず山からじゅうぶん離れた平地に立ちます。このとき山からの水平距離を測っておきます。まあ歩数でもだいたいの距離はわかるでしょう。
いまは例として5km(5000m)だったとします。
つぎにそこから山を見上げます。ここで分度器か測量機などで、見上げた角度を測ります。
例として24°だったとします。
ここで三角比のうち、タンジェントに登場ねがいます。
タンジェントの定義から、次の等式が成り立ちます。$$tan24° = \frac{h}{5000}$$
この式を変形して、$$h = 5000 \times tan24°$$
ここで\(tan24°\)はすでにヒッパルコスが計算してくれています。「三角比の表」によると、\(tan24° = 0.4452\)です。これを代入して、$$h = 5000 \times 0.4452 = 2226$$
これで、山の高さが2226mとわかりました。
このようにして、三角比をつかって遠い山の高さを測ることができるんですね。
地球の半径を測る
つぎにヒッパルコスが地球の半径を測った方法を紹介します。
下の図でいうと、\(r\) の値を求めることになります。
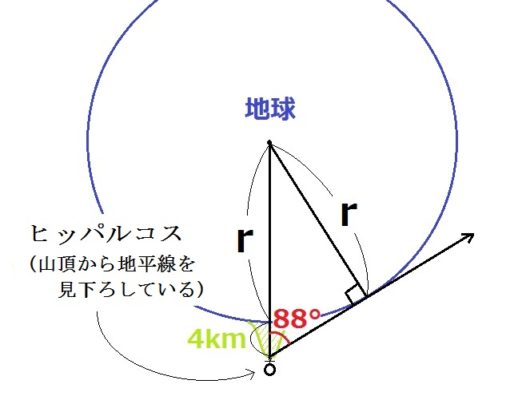
まずヒッパルコスは高い山の頂上にのぼり、そこから地平線を見下ろしました。
いま仮に山の高さは4km、見下ろした角度は88°としましょう。
山の高さは前掲の方法で測れるし、角度はやはり分度器か測量機で測れます。
じつはこれだけで、地球の半径を求めることができます。今度はサインの出番です。
サインの定義により、次の式が成り立ちます。$$sin88° = \frac{r}{r+4}$$
\(sin88°\)は「三角比の表」より、0.9994です。代入して、$$0.9994 = \frac{r}{r+4}$$
これ、\(r\)についての1次方程式ですね。中1の知識で解けます。んで解くと、$$r = 6662.666・・・$$
地球の半径は約6663kmとわかります。
(現代の精密な観測では、地球の半径は約6400kmです)。
いまから2200年も前に、計算だけで地球の半径を測っちゃったんですね。
三角比というのがどれだけ役に立つ強力な武器であったか、わかると思います。
月までの距離を測る
最後に、ヒッパルコスが月までの距離を測った方法も紹介しましょう。
下の図でいうと、\(d\) の値を求めることになります。
話を単純にするために、ヒッパルコス自身の方法とはすこし変えていますが、本質はたいして変わりません。
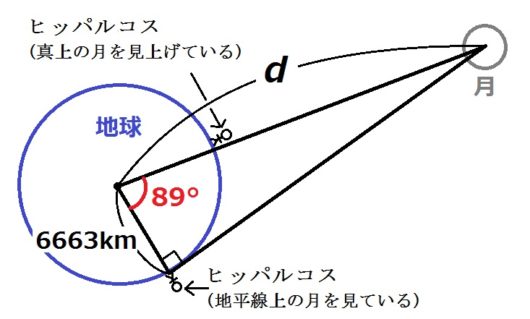
まずヒッパルコスは地球上を移動して、月が同じ位置にあるときに、2回、月を見ます。
一度は月が真上に来たとき(=南中したとき)に、もう一度は月が地平線に隠れるかどうかというときに見ます。
ちなみに「月が同じ位置」という条件は、そうじゃないと、上図のような固定した三角形をイメージできないからです。月って地球の周りを回ってますからね。
こうして2回月を見てから、ヒッパルコスはそれぞれの地点での緯度の差を出しました。
さいわいヒッパルコスは、いまいる地点の緯度を出す方法を知っていました。
この緯度の差というのが、上図の赤い角度になります。いまは89°としておきます。
また地球の半径はさっき計算したように、6663kmとしておきます。
これで準備が整いました。今度はコサインに登場してもらいます。
コサインの定義により、次の式が成り立ちます。$$cos89° = \frac{6663}{d}$$
\(cos89°\)は「三角比の表」より、0.0175です。代入して、$$0.0175 = \frac{6663}{d}$$
式を変形して、$$d = \frac{6663}{0.0175}$$
んでこれを計算すると\(d = 380742.85714\)、約38万kmと出てきます。
(現代の精密な観測では、地球と月の距離は約38.5万km)。
三角比を使うことで、地球と月の距離まで測れるんですね。
ピラミッドの高さを計算したり、いろんな地点までの距離を測って地図を描いたりできるのは、いわずもがなです。
こうした測量に、三角比がおおいに役に立つのです。
三角比はいまどう応用されているのか

ここまで、三角比の歴史と成り立ち、どのように役に立ってきたかを解説しました。
では、21世紀の現代において三角比はどのように使われているんでしょうか?
じつは測量をはじめ、設計や建築などの分野でバッチリ役に立っています。
そのひとつの例として、日本の国土地理院が三角比を使ってどのように地図を作製しているかを見ていきたいと思います。
ただ、じっさいに地図を作製するときには、正弦定理や、加法定理などを使います。
だって、地形を見ていて、直角三角形がそう都合よくいつも出てくるわけじゃないからです。上でみた3つの例はむしろ特殊です。
じっさいは直角のない、ただの三角形から、辺の長さを求めなければいけません。
だから正弦定理や加法定理などを使って、ちょっとした計算が必要になるんですね。
そこでまず、正弦定理や加法定理がどのように出てきたのか、歴史の流れにそって証明して、それから地図作成の例を見てみたいと思います。
んで、記事が長くなったのでそれは次回に!
→次の記事:三角比はいまどんな職業で役に立っているのか?地図製作を例に解説する
[この連載の記事一覧]
- 三角比とはなんだ?何の役に立つ?どんな歴史があるの?
- 三角比はいまどんな職業で役に立っているか?地図製作を例に解説する
- ド文系が「三角比の拡張」と「ラジアン」をわかりやすく解説する
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する①
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する②
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する③(2019/12完結!)




コメント
「三角比をつかって山の高さを測る」の項でつまずきました。「このとき山からの水平距離を測っておきます。」?図では山頂の真下からの距離になってますが、山頂の真下(山頂から地面に垂直に下がった直線と直角になる点)は現実にどうやって知ることができるのですか?
鋭いご質問ありがとうございます。
説明の流れ上省きましたが、山からの水平距離もまた、三角比を使った測量つまり「三角測量」で測ったのだと思われます。
三角測量の方法は次の記事「三角比はいまどんな職業で役に立っているか?地図製作を例に解説する」でくわしく解説しています。
主さんupお疲れ様です。
このサイトを見て三角関数が理解できました
よければですが、『フェルマーの最終定理』を噛み砕いて分かりやすく説明していただきたいです!
下と同じ人かな?
ありがとうございます。
「フェルマーの最終定理」ですか。
それ自体については、サイモン・シンの著作を超える「わかりやすい説明」はないと思いますが、数学の歴史という連載のなかで触れる予定ではおります。
いま現在のフェミニズムの思想史の連載を終えたら、とりかかるかも、です。
すぐ知りたい場合は上述の本がおすすめです。
主さん、わざわざありがとうございます。
これを見てずーっと分からなかった三角関数が少し理解できました。
リクエストなんですが『フェルマーの最終定理』を分かりやすく説明して欲しいです!
[…] 三角比とはなんだ?何の役に立つ?どんな歴史があるの? […]
分数が逆です(サインとかの意味のところの)
ご指摘いただき確認しましたが、正しいようです。
どこが逆になってますか?
aを斜線bを高さcを底辺とすると
sinθは斜線分の高さ
cosθは斜線分の底辺
tanθは底辺の高さ
で求めることができるはずなので問題ないと思います。
その通り。困るね。
何様のつもりですか( 主さん、これでサインコサインタンジェントが何故高校で教えられるか納得出来ました、ありがとうございます┏○ペコッ