三角比について3回目の記事になります。
これから、三角比の発展ヴァージョンである「三角関数」がどんな分野でどんな役に立っているかを見ていきます。
ただそのためにはまず、「三角関数」をおさらいする必要があります。
そして三角関数のためには、「三角比の拡張」と「ラジアン」を理解しとかないといけません。
ってことで、今日は「三角比の拡張」「ラジアン」の2つを復習します。
じゅうぶん理解してるよって人は読み飛ばしてかまいません。
逆に「ラジアンって何の意味があるの?」なんて人にはおススメの記事になります。
≪連載記事一覧≫
- 三角比とはなんだ?何の役に立つ?どんな歴史があるの?
- 三角比はいまどんな職業で役に立っているか?地図製作を例に解説する
- ド文系が「三角比の拡張」と「ラジアン」をわかりやすく解説する
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する①
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する②
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する③(2019/12完結!)
スポンサーリンク
三角比の拡張
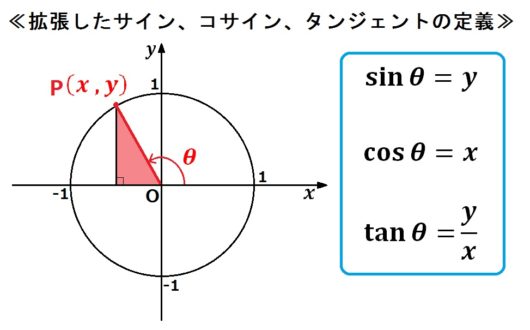
前々回の記事で、サイン・コサイン・タンジェントを直角三角形で定義しました。
でもそれでは、θの角度が0°~90°のあいだでしか使えません。
(正確には \(0°<θ<90°\))
120°とか、330°とか、1万°でもOKにしたほうが数学としては扱いやすいわけです。
また古代から中世にかけてインドとイスラーム教圏で数学が発展すると、「0」という数も出てきて、さらには「マイナス」という概念も出てきました。
となると、数学者は「-90°」とかも扱いたくなるんです。
そこで、すべての実数を扱えるようにθの角度を拡張して、同時にサイン・コサイン・タンジェントの定義も新しくしたのが「三角比の拡張」です。
座標上の単位円で直角三角形を考える
拡張のしかたを以下、ちょっとくわしく見てみます。
まず上図のように、座標上に半径1の円を描きます。円の中心は原点にします。
(この円を数学用語で「単位円」といいます)
そんで円周上に点Pをとります。どこでもいいんですが、わかりやすいように右上あたりにとっておきます。
すると上図のような、ピンクの直角三角形ができますね。
点Pの座標を(x , y)とすると、底辺がx、高さがy、斜辺の長さが1の直角三角形です。
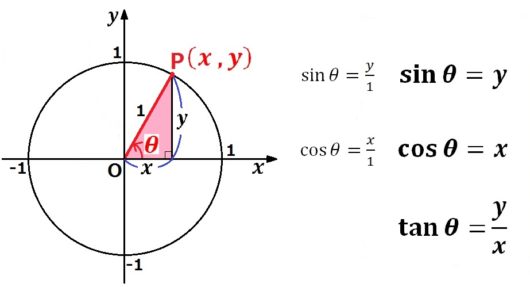
ここでサイン、コサイン、タンジェントの最初の定義より、$$sinθ = \frac{y}{1}、cosθ = \frac{x}{1}、tanθ = \frac{y}{x}$$となります。
こうして、$$\large{sinθ = y、cosθ = x、tanθ = \frac{y}{x}}$$という新しい定義が出てくるんです。
新しい定義の意味
このように定義しなおすと、
- sinθは点Pのy座標
- cosθは点Pのx座標
- tanθは直線OPの傾き
という意味になります。
じゃあべつに、点Pが左上にいても、左下にいても、右下にいても、それぞれsinθ・cosθ・tanθが表せますよね。
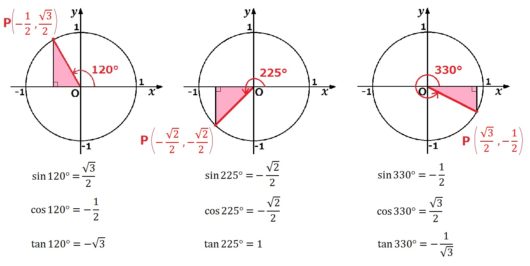
つまり例えばこういうこと↓
こうして、どんな角度でもサイン・コサイン・タンジェントが使えるようになったのでした。
もちろんマイナスもいけます、逆回りにぐるっとさせればいいわけだから。
ラジアンとは何か
次に、角度の表し方を変更します。
いままでは「60°」とか「330°」のように、一周を360等分した表示で角度を表していました。
これを「度数法」といいます。
でも度数法では、あとあと、三角関数を計算したり公式を書いたりするときに不便なんです。
(どう不便かは後で説明します)
そこで角度の新しい表し方、ラジアンが登場します。
このラジアンを使った角度表示を「弧度法」と呼びます。
ラジアンの定義
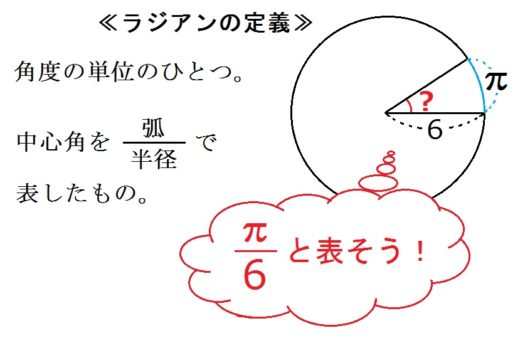
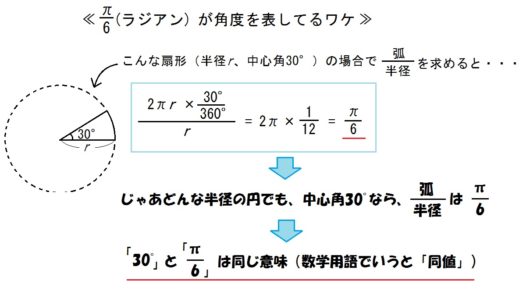
上図に掲げたとおり、ラジアンとは円の中心角を\(\frac{(弧)}{(半径)}\) で表したものです。
たとえば上図では、中心角は「\( \frac{π}{6}\) ラジアン」です。
ただうしろの「ラジアン」は省略することが多いですね。たんに「\( \frac{π}{6}\)」と書く場合がほとんどです。これで角度のことを言ってます。
なぜ半径と弧という2つの長さから、角度が表せるのか?
それは↓を見ればわかります。
式から半径 r が消えてなくなったでしょ。
だから大きさに関係なく、中心角30°の扇形なら、\( \frac{弧}{半径}\) はつねに\( \frac{π}{6}\) なんです。
じゃあ30°と\( \frac{π}{6}\) っておんなじことやん。
もういっそのこと、30°っていう表記はやめて、これからは角度を\( \frac{π}{6}\) って表そうや。
これが弧度法の発想なんですね。
度数法と弧度法の関係
弧度法では、180°がちょうど\(π\) (ラジアン) になります。
半円を考えて、\( \frac{弧}{半径}\) を計算してみればすぐわかります。
当然、360°は2\(π\)、540°は3\(π\) となります。
また90°は\( \frac{π}{2}\) ですね。
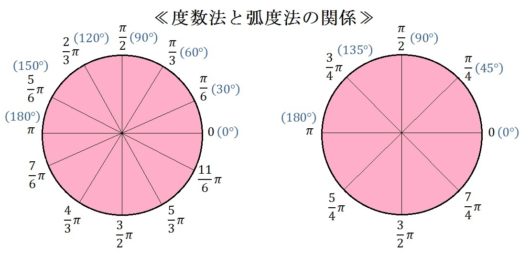
よく出てくる角度を下図に載せます。ついでに度数法での角度も併記しときます。
ちなみに、度数法の角度を弧度法の角度になおすには、以下の式でかんたんに求まります。$$\large{\frac{π}{180}x°} (x°は度数法での角度)$$
これは$$\begin{eqnarray}(弧度法の角度)&=& \frac{弧}{半径} = \frac{2πr × \frac{x°}{360}}{r} \\ &=& \frac{π}{180}x°\end{eqnarray}$$というようにして求まります。
これを使えば、たとえば度数法で30°の角度は、$$\frac{π}{180} × 30° =\frac{π}{6}$$ と出てきますね。
おぼえておいて損はない式です。
なぜ弧度法を使うのか?
さっき、「度数法ではあとあと、三角関数を計算したり公式を書いたりするときに不便」と書きました。
どう不便か、かんたんにいうと、三角関数の極限や微分を計算するときに不便なんです。
こちらのサイトにうまくまとめてありましたので、ジュウゴも参考にさせてもらいました。
→「高校数学の美しい物語 度数法ではなく弧度法を使うメリット」
ただサイトにもあるように、三角関数の極限や微分って、数Ⅲの途中から出てくるやつです。
数Ⅱ・数Bで終えたド文系のジュウゴには、だから弧度法を使う意味がよくわからなかったんですね!
このブログでは三角関数の極限や微分は取扱いません。
(三角関数の分野はフーリエ級数展開までとする予定です)
ただジュウゴの勉強がすすんだら、いつか書くかもしれません。
ってことで、数十年後のいつかのために(!)、次の記事からは弧度法の表記でいきます。
次回は「三角関数のグラフ」のおさらいです。
→三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する①
≪連載記事一覧≫
- 三角比とはなんだ?何の役に立つ?どんな歴史があるの?
- 三角比はいまどんな職業で役に立っているか?地図製作を例に解説する
- ド文系が「三角比の拡張」と「ラジアン」をわかりやすく解説する
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する①
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する②
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する③(2019/12完結!)


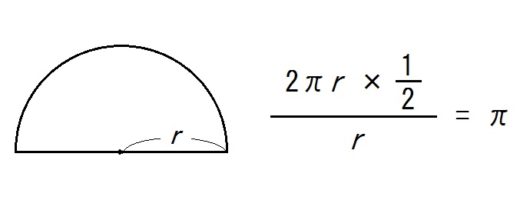



コメント
三角比の拡張を授業で取り扱ったい、何故θがその位置になるのかどうしても理解できなかったのですが、こちらの記事を拝見してなんとなく理解することができました。ありがとうございます。参考にして期末テストを乗り越えます。
解りやすく解説されていて、度数法と弧度法の関係を
理解することが出来ました。
有難うございました。
72歳