三角比・三角関数についてラストの記事になります。
ずっと放置してしまってましたが、2年半ぶりの更新!
いよいよフーリエ級数を最後まで理解していきましょー。
連載が完成していないことをすっかり忘れてました、コメントで指摘してくださった方、ありがとうございます。
≪前回までの記事≫
前回までの復習
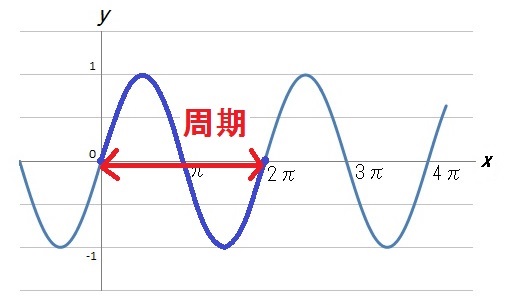
この連載は「三角比や三角関数がいったい何の役に立つのか」を明らかにするものでした。
三角比については、1,2回目の記事でみたように、測量などに役立つ。
三角関数については、3,4,5回目の記事でみてきたように、音波や心電図などのあらゆる波(=周期的な関数)を分析するのに役立つ、という話でした。
そしてどんなに複雑な波の形でもサインとコサインの足し算だけに分解できる、それを可能にするのが「フーリエ級数」だと。
それで前回からフーリエ級数の内容を理解してきたわけです。
前回わかったのは、
- フーリエ級数とはコサインとサインを何度も足し合わせたもの
- コサインとサインの係数はそれぞれ、なんらかの数列である
- \(x\) の前の数字は1,2,3…と1ずつ増えていく
という3点。
式の形としては、
$$f(x) = \displaystyle \sum_{ n = 1 }^{ 7 } [ a_n \cos nx + b_n \sin nx ]$$
まで到達しました。つまりバラして書けば、
\begin{eqnarray} f(x) &=& a_1 \cos x + b_1 \sin x \\ &+& a_2 \cos 2x + b_2 \sin 2x \\ &+& a_3 \cos 3x + b_3 \sin 3x \\ &+& a_4 \cos 4x + b_4 \sin 4x \\ &+& a_5 \cos 5x + b_5 \sin 5x \\ &+& a_6 \cos 6x + b_6 \sin 6x \\ &+& a_7 \cos 7x + b_7 \sin 7x \end{eqnarray}
までは理解できたわけです。
しかし、まだフーリエ級数の形にはなっていません。
フーリエ級数になるためには、
○\(n\) が7までじゃなくて\(\infty \)(無限)まで足す?
○\(nx\) の前に \(\frac{2\pi}{L}\) なんてのがあるぞ!?
○先頭に \(\frac{a_0}{2}\) がくっついてるぞ!
という3匹の敵をやっつける必要があります。
以下、ひとつひとつやっつけます。
数Ⅱ・Bで勉強をやめた文系の人にもわかりやすく説明していきます。
では!
無限に足し算するのはなぜ?

まず1つめの「無限に足し算するのはなぜか」という理由を解説します。
さきに結論をいえば、それは求める完成形に限りなく近づくためです。
フーリエ級数を使う場面とは
フーリエ級数が実際に使われる場面。
それはたとえば、交響曲をデジタル録音して再生したい場合などです。
コンサートホールにマイクを設置して、音を拾ったら、ある瞬間の音波が下図のようになったとしましょう。

こんな複雑な波のままでは、コンピュータでは処理できません。
コンピュータってのは、複雑なものを単純な要素に分解してやってはじめて「わかった!」となるヤツだからです。
そこで、フーリエ級数の出番です。
この複雑な波を、一個一個コサインとサインの単純な波に分解していって、それらを全部足す。
そうするとコンピュータはこの複雑な形を再現できるようになります。
このとき、足し合わせる要素が多ければ多いほど、もとの波の形に近くなります。
つまり7個よりも10個、100個よりも1000個足し合わせるほど、録音時の音を忠実に再現できるようになります。
では、もとの音を完璧に再現するには?
そう、無限に足せばいいんです。
これがフーリエ級数において「無限に足し算する」理由です。
足せば足すほど完成形に近づく
つまり、フーリエ級数を使うのは、もともとある完成形があって、それを単純な要素の足し算で再現するとき。
このとき、足し算する数が多ければ多いほど完成形に近づく。
だから、数式の上では「無限に足す」ことにしておいたんです。
このことを、以下のグラフで示してみましょう。
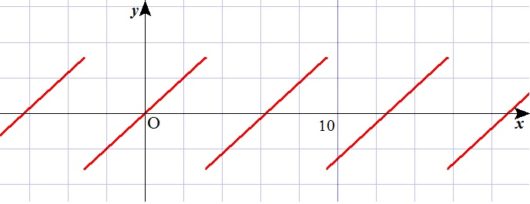
このグラフは
$$ f(x)=x \quad (-\pi \leq x \leq \pi) $$
という関数を周期的に描いたものです。
この完成形に、コサインとサインの足し算、つまりフーリエ級数で迫ってみましょう。
$$ f(x) = \displaystyle \sum_{ n = 1 }^{ a } \left[(-1)^{n+1} \frac{2}{n} \sin nx \right] $$
関数の式はこれです。係数どうやって決めたんじゃ!とかは後で説明しますんで、とりあえず置いといて。
まず3回ほど足してみます。つまり \(a=3\) のとき。
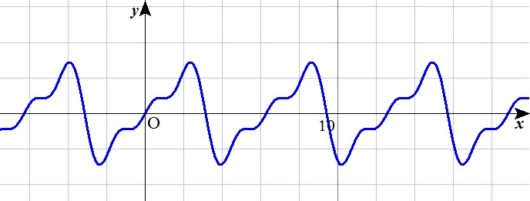
んー、まだまだ。
じゃ10回ほど足してみます。つまり \(a=10\) のとき。
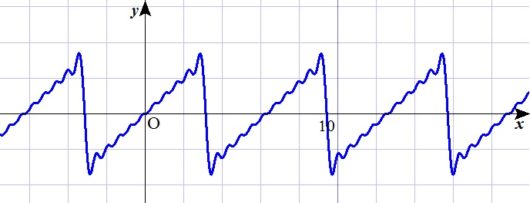
けっこう近づいた?
つぎ、30回ほど足します。
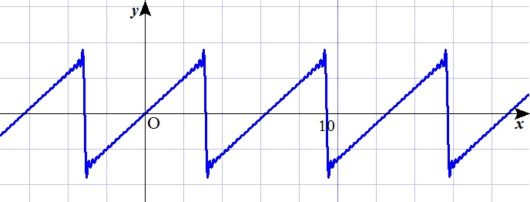
かなり近い!
最後、100回足しちゃえ。
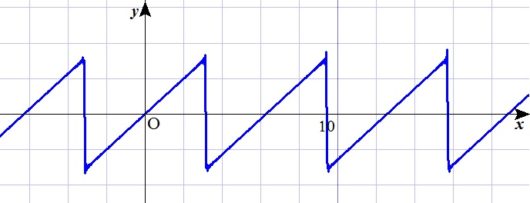
どうですか?
足せば足すほど完成形に近づくことがイメージできたのでは。
以上のように、なぜフーリエ級数では無限に足し算するのか?
その理由は「求める完成形に限りなく近づけるため」なのでした。
級数の収束
ただ中には「無限に足し算したら答えはぜんぶ無限大になるんじゃないの!?」って人もいると思います。
そういう人にむけて、ちょっと余談を。
大丈夫、無限大にならない数列もあります。
たとえば以下の数列など、そうです。
$$ 1 , \frac{1}{2} , \frac{1}{4} , \frac{1}{8} , \frac{1}{16} \quad \mbox{……} $$
この数列を無限に足すと、答えは「2」になります。
$$ 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} \quad \mbox{……} = 2 $$
なぜか?下の図をみればわかります。
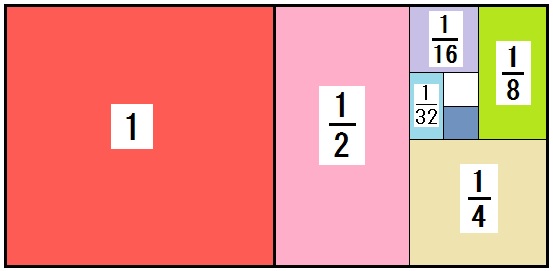
このように、数列の無限の足し算を「級数」、それがある値に収まることを「収束する」といいます。
数Ⅲで習う数学用語なんで、ほんとは出すつもりじゃなかったんですが、余談だから許してください。
この用語を知れば、なぜ「フーリエ級数」と呼ばれるかもわかるから……。
以上、フーリエ級数の \( \displaystyle \sum \) に \( \infty \) がある理由でした。
≪前回までの記事≫
\(\frac{2\pi}{L}\) ってなんなの?

次に、2つめの「\(nx\) の前の \( \frac{2\pi}{L}\) って何?」という疑問にお答えします。
これも先に結論からいえば、いろんな周期を扱えるようにするための工夫です。
\(nx\) では扱える周期が \(2\pi\) だけ
4回目の記事で復習したように、\(y=\cos x\) や \(y= \sin x\) の周期は \(2\pi\) でした。
フーリエ級数では、この \(2\pi\) というはじめの周期が、あとに続くすべての式の基準になります。
だって、フーリエ級数って
\begin{eqnarray} f(x) &=& a_1 \cos x + b_1 \sin x \\ &+& a_2 \cos 2x + b_2 \sin 2x \\ &+& a_3 \cos 3x + b_3 \sin 3x \\ &+& \quad \mbox{……} \end{eqnarray}
って続くので、
- 2行目の式の周期は「\(2\pi \) の \(\frac{1}{2}\)」
- 3行目の式の周期は「\(2\pi \) の \(\frac{1}{3}\)」…
となるから。
グラフでみれば、たとえば以下のような感じですね。
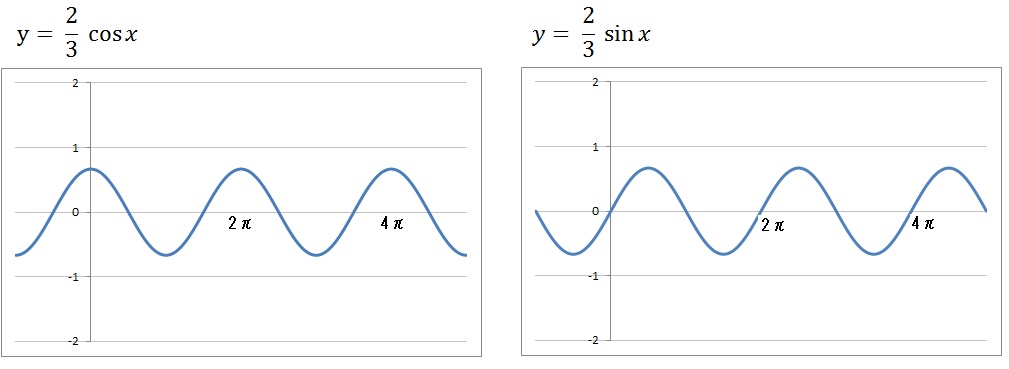
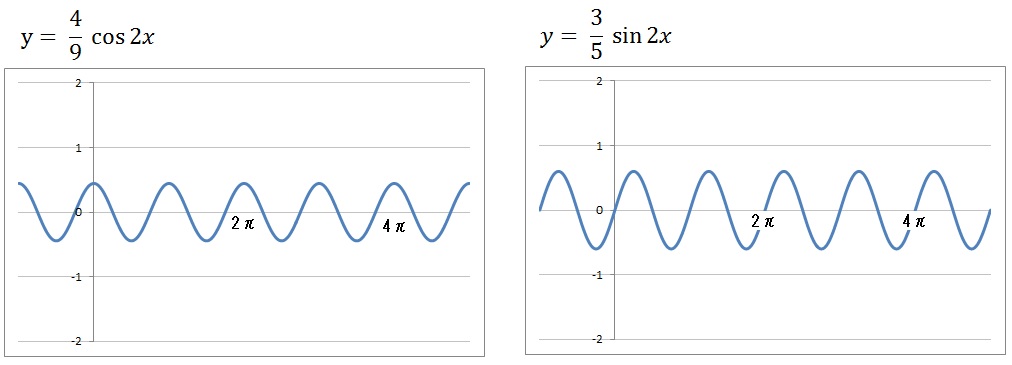
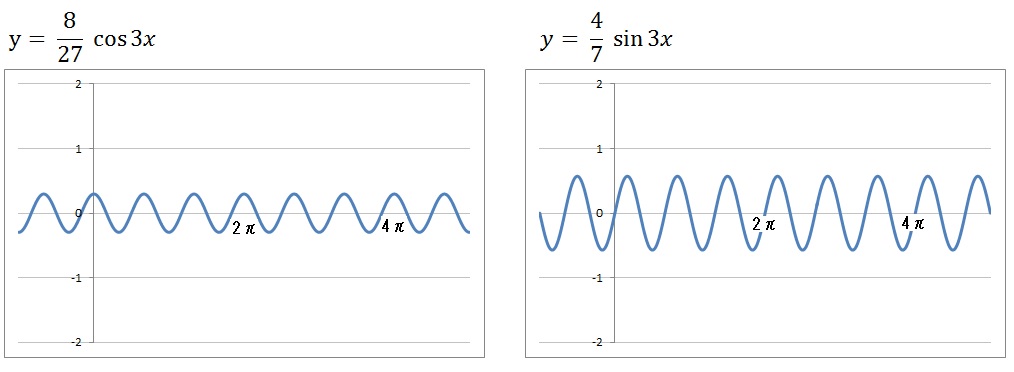
つまり
$$f(x) = \displaystyle \sum_{ n = 1 }^{ \infty } \left[ a_n \cos nx + b_n \sin nx \right]$$
という数式のままでは、周期が \(2\pi\) の波しか扱えないのです。
当然、できあがる波の形も \(2\pi\) の周期のものだけになります。
(\(x\) の係数は周期の逆数を表すんでした。ここまでの話が頭に入らない人は、3,4,5回目の記事を適宜復習してください)。
もっといろんな周期を!
でもこれじゃ何かと不便です。
たとえば、心電図。
1回の心拍はだいたい0.8秒(= \(\frac{4}{5}\)秒)なんで、\(\frac{4}{5}\pi\) とかの周期でも波が描きたい!
それに、ラジオとかの周波数。
Hzって1秒が基本単位なんで、\(1\pi\) の周期でも扱えるようにしたい!
そこで \(\frac{2\pi}{L}\) の出番です。
この式の \(L\) は「周期」を表しています。
つまり、あなたの扱いたい周期を \(L\) に代入することで、どんな周期の波でも自由に描けるようになるのです。
\(L\) ではなく \(T\) と書いている参考書もあります。
フーリエ級数
\(L\) に好きな周期を入れてみよう
たとえば \(1\pi\)(\(\pi\))周期の波を描きたいとします。
\(\frac{2\pi}{L}nx\) に \(L=\pi\) を代入すると
$$ \frac{2\pi}{\pi}nx = n \cdot 2x $$
となり、フーリエ級数は
\begin{eqnarray} f(x) &=& a_1 \cos 2x + b_1 \sin 2x \\ &+& a_2 \cos 2 \cdot 2x + b_2 \sin 2 \cdot 2x \\ &+& a_3 \cos 3 \cdot 2x + b_3 \sin 3 \cdot 2x \\ &+& \quad \mbox{……} \end{eqnarray}
と、\(2x\) 基準で式が展開していきます。
つまり周期は \(2\pi \times \frac{1}{2} = \pi \) が基準となります。
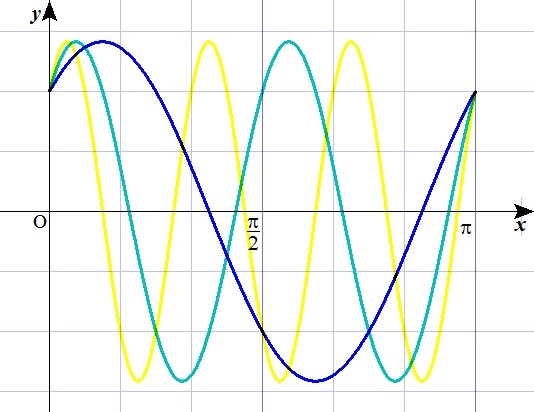
また、\(\frac{4}{5}\pi\) 周期で波を描きたい場合。
\(\frac{2\pi}{L}nx\) に \(L=\frac{4}{5}\pi\) を代入すると
$$ \frac{2\pi}{\frac{4}{5}\pi}nx = n \cdot \frac{5}{2}x $$
となり、フーリエ級数は
\begin{eqnarray} f(x) &=& a_1 \cos \frac{5}{2}x + b_1 \sin \frac{5}{2}x \\ &+& a_2 \cos 2 \cdot \frac{5}{2}x + b_2 \sin 2 \cdot \frac{5}{2}x \\ &+& a_3 \cos 3 \cdot \frac{5}{2}x + b_3 \sin 3 \cdot \frac{5}{2}x \\ &+& \quad \mbox{……} \end{eqnarray}
と、\(\frac{5}{2}x\) 基準で式が展開していきます。
つまり周期は \(2\pi \times \frac{2}{5} = \frac{4}{5}\pi \) が基準となります。
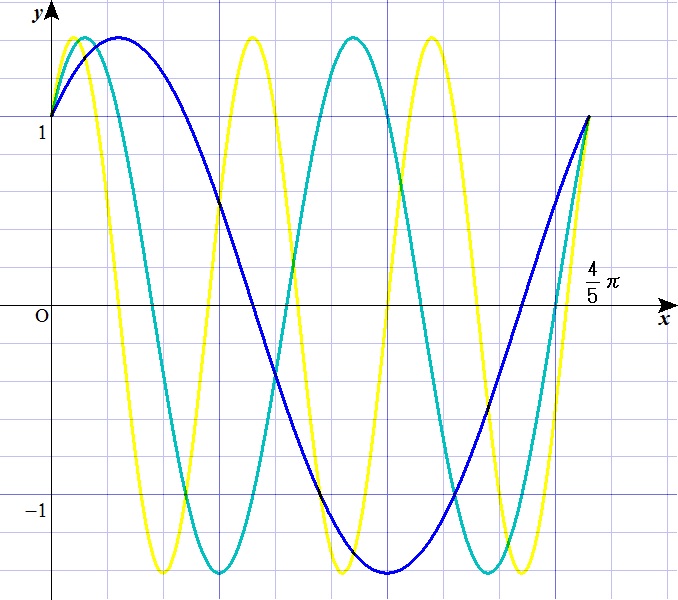
以上のように、なぜフーリエ級数に \(\frac{2\pi}{L}\) という文字があるのか?
それはいろんな周期を扱えるようにするための数学上の工夫だったのです。
*もちろん、周期が \(2\pi\) のままでよければ \(\frac{2\pi}{L}\) なんて必要ありません。このあとの話でも、数式をスッキリするために省略しておきます。
≪前回までの記事≫
\(\frac{a_0}{2}\) がくっついてる?

最後に、フーリエ級数の先頭にある \(\frac{a_0}{2}\) というヤツの意味を解説します。
これは「関数の平均値」を表しています。
ん?なんじゃそりゃ?
順をおって説明していきますね。
関数の平均値とは?
たとえば \(y=2+ \sin x\) という関数は以下のグラフでした。
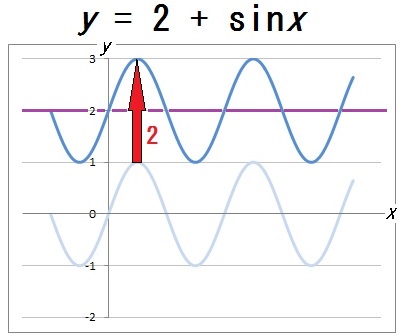
このときの「2」という値を、この関数の平均値といいます。
つまり関数の平均値とは、風がないときの水面の高さのこと。
風が立って波ができて、もともとの水面の高さから上下したりしますが、もし風がなければこの高さにおちつくよー、っていう値のことです。
だから \(y=\sin x\) とか \(y=\cos 2x\) とかの関数の平均値は「0」です。
定数が加えられてないからね。
フーリエ級数における \(\frac{a_0}{2}\) もまた、定数です。
よって、フーリエ級数に \(\frac{a_0}{2}\) がある意味。
それは水面の高さをいろいろに設定できるようにするためです。
これが無ければ、フーリエ級数で描く波はすべて水面の高さが「0」(つまりx軸)に限られてしまうのです。
なぜ「平均値」といえるのか
ただここで、「関数の平均値」という言葉に納得できない人もいるでしょう。
関数に平均があるなんて習わなかったぞ!と。
そこで、なぜ水面の高さが「関数の平均値」といえるのか、そのワケを例を使ってちょっと詳しくみてみましょう。
以下の棒グラフは、A,B,C,D,E,F君の6人が10点満点のテストをしたその結果です。
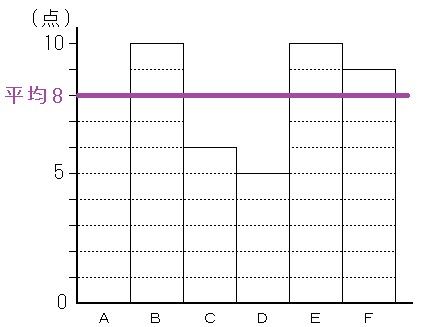
点数が順に8点,10点,6点,5点,10点,9点だったとすると、その平均は
$$(8+10+6+5+10+9) \div6 =8 $$
と求まります。
この平均値「8」に線を引いておきました。
さて、6人それぞれの点数がこの平均値からどれだけ離れているか、+ーで書き加えます。

すると+-の合計は差し引き0になりますね。
だから、この棒グラフの上をつないで関数のように見立てた場合、「8」は関数の平均値といえるんです。
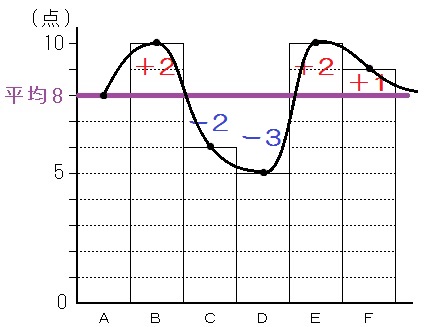
フーリエ級数における平均値の求め方
これで \(\frac{a_0}{2}\) が関数の平均値といえる理由はOKですね。
しかし、もうひとつ大きな疑問が残ります。
「なんで \(\frac{a_0}{2}\) という形なんだ?」
「定数なら \(c\) と単純に書けばいいだろう?」
って疑問です。
こいつを最後にやっつけますので、もうすこしだけお付き合いください。
話をわかりやすくするために、フーリエ級数という関数の平均値を \(c\) としておきます。
$$f(x) = c + \displaystyle \sum_{ n = 1 }^{ \infty } \left[ a_n \cos \left( \frac{2\pi}{L}nx \right) + b_n \sin \left( \frac{2\pi}{L}nx \right) \right]$$
まず、ちょっと寄り道して、\(c\) の求め方から。
平均値 \(c\) は定積分を使えば求まります。
積分って、数Ⅱでやった、曲線で囲まれた面積を求めるとかのアレです。
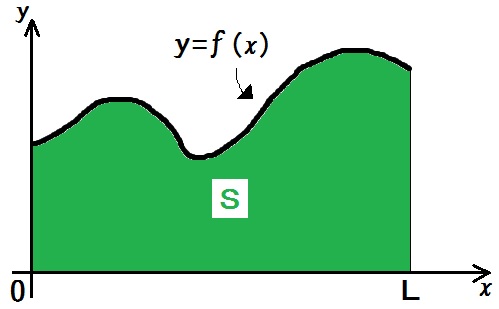
そもそもこんな面積をどうやって求めているかというと、細かく縦割りして足しています。
つまり、かぎりなく細い棒グラフを無数につくって、それらをぜんぶ足しているんです。
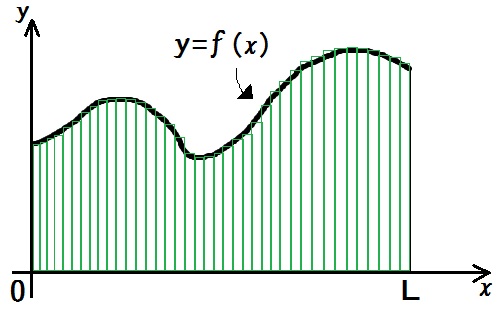
これが積分の考え方、つまり
$$ S= \displaystyle \int_0^L f(x) dx$$
の意味です。
では、これら棒グラフの平均値はどうやったら求まりますか?
そう、面積\(S\) を \(L\) で割ればいいね。
6人のテストの平均点は合計を6で割ったように。
よって、
$$ c= \frac{1}{L} \displaystyle \int_0^L f(x) dx $$
これがフーリエ級数における定数項 \(c\) の求め方になります。
謎が解けるまであと少しです。
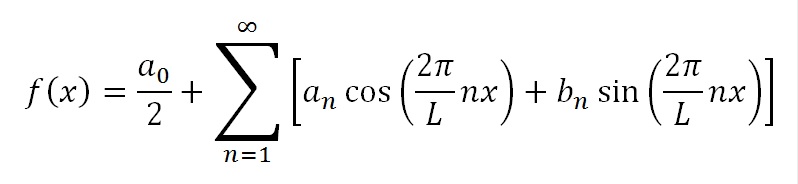
フーリエ級数
\(\frac{a_0}{2}\)となる理由
\(c\) の求め方につづいて、\(a_n\) と \(b_n\) の求め方も紹介します。
いきなり数式を出しちゃいますが、これです。
$$ a_n = \frac{2}{L} \displaystyle \int_0^L f(x) \cdot \cos nx dx $$
$$ b_n = \frac{2}{L} \displaystyle \int_0^L f(x) \cdot \sin nx dx $$
フーリエ級数のなかで、コサインとサインそれぞれの係数となっている \(a_n \) と \(b_n\) 。
その数列の一般項はこれで求められるのです。
*話を単純にするために \(\frac{2\pi}{L}\) は省いています。
*なぜこれで \(a_n \) と \(b_n\) が求まるのか、その理由はこの記事の最後に記します。

\(a_n\) の式をちょっと変形すると、こうなります。
$$ \frac{a_n}{2} = \frac{1}{L} \displaystyle \int_0^L f(x) \cdot \cos nx dx $$
んで \(n=0\) を代入してみます。
$$ \frac{a_0}{2} = \frac{1}{L} \displaystyle \int_0^L f(x) \cdot \cos 0 dx $$
\(\cos 0 =1\) だから↓
$$ \frac{a_0}{2} = \frac{1}{L} \displaystyle \int_0^L f(x) dx $$
…あれ?この右辺…
…どっかで見たよね?
$$ c= \frac{1}{L} \displaystyle \int_0^L f(x) dx $$
まったく同じやん!
ってことで
$$ c= \frac{a_0}{2} $$
となるのでした。
数学者ってのはなぜか「数式に登場する文字はできるだけ少ないほうがいい」というマナーを守ります。
なので、フーリエ級数の最初の定数項も \(a_n\) で表しているんです。
以上、なぜ \(\frac{a_0}{2}\) がくっついてるのか?
その理由は関数の平均値だから。
そしてその平均値が \(a_n\) で表せちゃったから、でした。
まとめ

おつかれさまでした。
まとめます。
この記事のまとめ
フーリエ級数ではなぜ「無限に足し算」するのか?
それは、足せば足すほど求める完成形に近づいていくため。
なので、数式上「\(\infty\)」としておいた。
フーリエ級数にはなぜ \(nx\) の前に \(\frac{2\pi}{L} \) というのがあるのか?
それは、いろんな周期を自由に扱えるようにするため。
\(L\) に好きな周期を代入すれば、その周期が基準となるように工夫した、それが \(\frac{2\pi}{L} \) 。
フーリエ級数にはなぜ \(\frac{a_0}{2}\) がくっついているのか?
それは、波の水面の高さ(=関数の平均値)を0以外でもOKにするため。
んで数式こねくりまわしたら \(\frac{a_0}{2}\) って形になったの、結果的に。
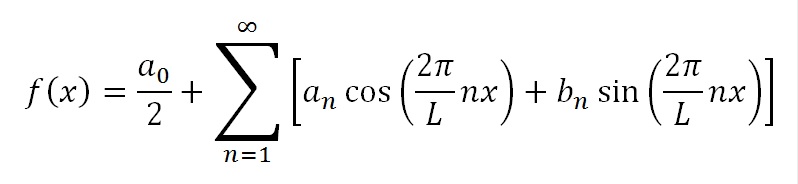
フーリエ級数
係数の求め方の導出
最後に、記事中でとばしていた \(a_n\) と \(b_n\) の求め方、つまり
$$ a_n = \frac{2}{L} \displaystyle \int_0^L f(x) \cdot \cos nx dx $$
$$ b_n = \frac{2}{L} \displaystyle \int_0^L f(x) \cdot \sin nx dx $$
こんなん出てくる理由を最後に説明します。
数学テクニックの話になりますが、本当に最後の最後なんで。
厳密さよりもわかりやすさ重視でいきますねー。
$$ f(x) = c+ \displaystyle \sum_{ n = 1 }^{ 7 } [ a_n \cos nx + b_n \sin nx ] $$
ってな感じの単純な式を用意します。つまり
\begin{eqnarray} f(x) &=& c \\&+& a_1 \cos x + b_1 \sin x \\ &+& a_2 \cos 2x + b_2 \sin 2x \\ &+& a_3 \cos 3x + b_3 \sin 3x \\ &+& \mbox{……} \\ &+& a_7 \cos 7x + b_7 \sin 7x \end{eqnarray}
こいつの両辺に \(\cos 7x\) をかける。
\begin{eqnarray} f(x) \cdot \cos 7x &=& c \cdot \cos 7x \\&+& a_1 \cos 7x \cdot \cos x + b_1 \cos 7x \cdot \sin x \\ &+& a_2 \cos 7x \cdot \cos 2x + b_2 \cos 7x \cdot \sin 2x \\ &+& a_3 \cos 7x \cdot \cos 3x + b_3 \cos 7x \cdot \sin 3x \\ &+& \mbox{……} \\ &+& a_7 \cos 7x \cdot \cos 7x + b_7 \cos 7x \cdot \sin 7x \end{eqnarray}
ここで「積→和の公式」を当てはめて
\begin{eqnarray} f(x) \cdot \cos 7x &=& c \cdot \cos 7x \\&+& a_1 \frac{1}{2}(\cos 8x + \cos 6x) + b_1 \frac{1}{2}(\sin 8x – \sin 6x) \\ &+& a_2 \frac{1}{2}(\cos 9x + \cos 5x) + b_2 \frac{1}{2}(\sin 9x – \sin 5x) \\ &+& a_3 \frac{1}{2}(\cos 10x + \cos 4x) + b_3 \frac{1}{2}(\sin 10x – \sin 4x) \\ &+& \mbox{……} \\ &+& a_7 \frac{1}{2}(\cos 14x + \cos 0) + b_7 \frac{1}{2}(\sin 14x – \sin 0) \tag{1} \end{eqnarray}
としておきます。
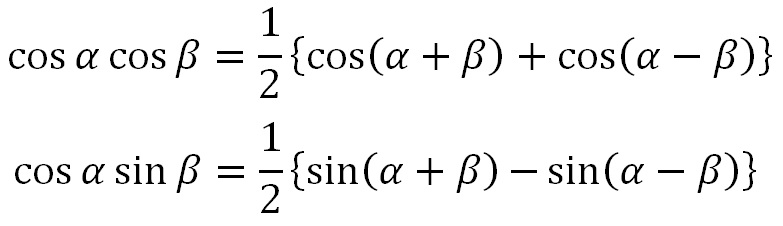
積→和の公式
ここから、(1)式の両辺の、\(0\)~\(L\) における平均値をとってみましょう。
まず左辺は
$$ \frac{1}{L} \displaystyle \int_0^L f(x) \cdot \cos 7x dx \tag{2}$$
この考え方は先に紹介した定積分ですね。
\(f(x) \cdot \cos 7x\) をひとつの関数とみて、平均をとるとこうなります。
次に右辺。
\(\cos7x\) の平均値は \(0\) だから、最初の行は \(0\) 。
\(\cos8x\) とか \(\sin6x\) とかの平均値も \(0\) だから、2行目も \(0\) 。
以下同様にしてほとんどが \(0\) ですが、最後の行だけ残ります。
最後の行は、\(\cos0 =1\) , \(\sin0 =0\) だから、
$$ a_7 \frac{1}{2}(\cos14x +1) + b_7 \frac{1}{2}(\sin14x -0) $$
1の平均値だけは \(0\) じゃなくて \(1\) ですね。
よって右辺の平均値は
$$ \frac{1}{2} a_7 \tag{3} $$
したがって、(2)(3)から、
$$ \frac{1}{L} \displaystyle \int_0^L f(x) \cdot \cos 7x dx = \frac{1}{2} a_7 $$
変形すれば
$$ a_7 = \frac{2}{L} \displaystyle \int_0^L f(x) \cdot \cos 7x dx $$
と出ます。
ところで、最初に \(\cos7x\) をかけてこうなったけど、\(7\) を \(n\) と一般化してやれば、
$$ a_n = \frac{2}{L} \displaystyle \int_0^L f(x) \cdot \cos nx dx $$
と、係数 \(a_n\) を求める式が導かれるのでした。
\(b_n\) についても理屈は同様です。
≪前回までの記事≫
長い旅でしたね。
三角比や三角関数が役に立っているワケを、ちょっとでもイメージできたなら幸いです。
ありがとうございました。
ご感想などお待ちしています。






コメント
>ここから、(1)式の両辺の、0~L における平均値をとってみましょう。
の意味が理解できません。
教えていただけますでしょうか。
左辺・右辺それぞれの関数において、xの変域0~Lにおける平均値をとった、ということです。
「0~L」と指定したのは、左辺の定積分が0からLまでとなるようにするための工夫です。
フーリエ変換の過程において、sin及びcosの係数の求め方も説明して頂けると嬉しいです。
とても丁寧な説明ありがとうございます。
理解しやすかったです。
フーリエ変換の全体像及び解を導くまでの過程が丁寧かつ親切で、
他の方にもお勧めです。
実践高校などで、数学を最後までやっていない自分にとって非常にありがたかったです。