中学数学「空間図形」⑤ 立体の切断問題のコツ

中１数学「空間図形」単元のさいごは、立体の切断問題を解説します。

ここでつまずく原因はおもに２つ。

• 切り口の図形がイメージできない
• 切断された立体の体積をどうやって求めたらいいかわからない

つまり、

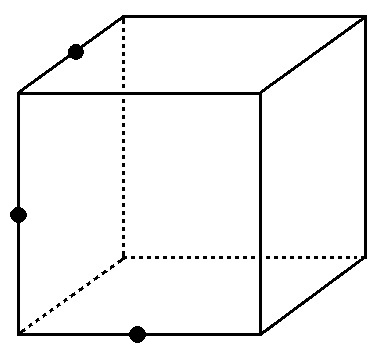
↑これが

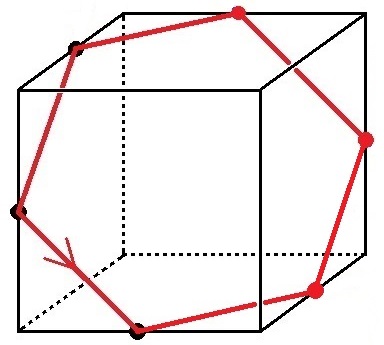
↑こんな切り口になるとイメージできない。

また、

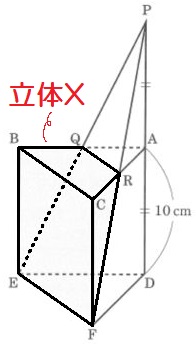
↑こんな立体の体積の求め方がわからない、というもの。

そこで以下では、

• 切り口の図形を描くコツ
• 切断された立体の体積の求め方

という２点を、豊富な例題とともに紹介します。

切断問題が苦手というすべての中学生に参考にしてください。

切り口の図形

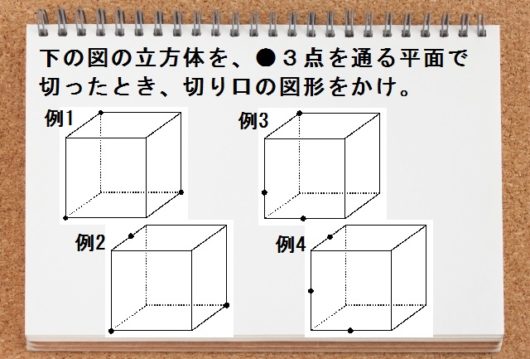
立方体や直方体を切断したときの切り口がどんな図形になるか？

これ、空間認識能力の高い人には理屈ぬきでイメージできるけど、そうでない人にはいつまでたってもわからない問題として立ちふさがります。

ただ、イメージできない人でもできるようになるコツがありました。

それは以下３つのルールに沿って描いていくことです。

1. 同じ面上の２点は結ぶ
2. 平行な面の切り口は平行になる
3. 面を延ばす

 

正三角形になる切り口

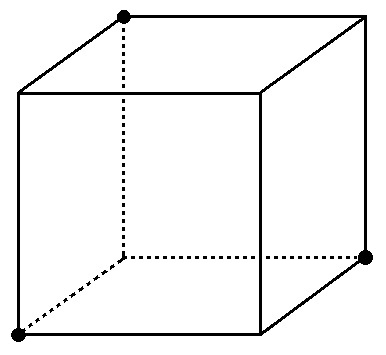
たとえばこの例題。

３つのルール

1. 同じ面上の２点は結ぶ
2. 平行な面の切り口は平行になる
3. 面を延ばす

を上から順に当てはめていけば、切り口が描けます。

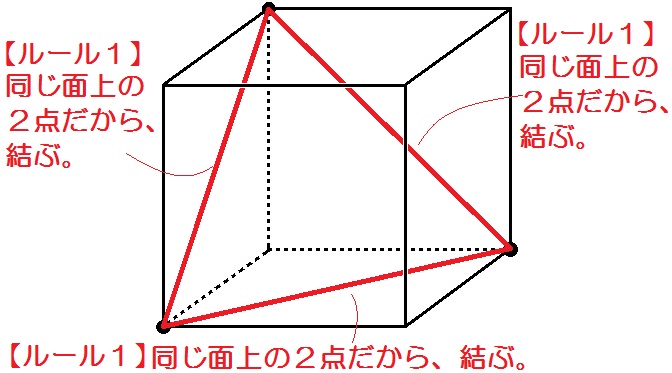
今回はどの２点を選んでも同じ面の上にあったので、ルール１だけでいけました。

切り口はごらんのとおり、正三角形になります。

ただ問題によってはルール１が当てはまらないときもある。

そんなときは次にルール２を適用します。

 

等脚台形になる切り口

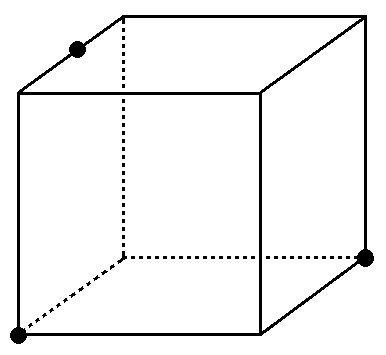
たとえばこの例題。

左と下は、同じ面上に２点があるので、ルール１に則って結べます。

でも、左上の点と右奥の点は同じ面上にないので、ルール１が当てはまらない。

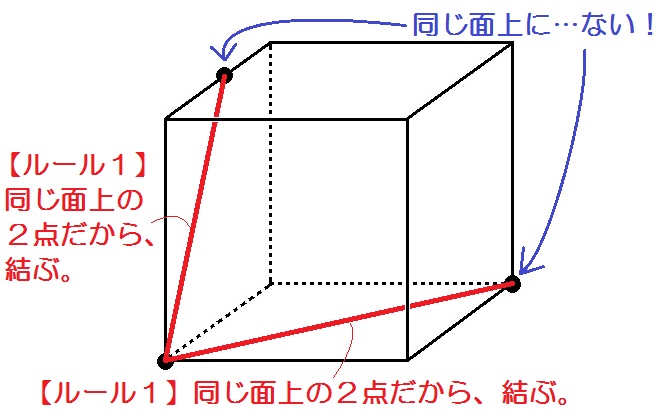
こんなときは以下のルールのうち２．を使う。

1. 同じ面上の２点は結ぶ
2. 平行な面の切り口は平行になる
3. 面を延ばす

つまりこんなかんじ↓

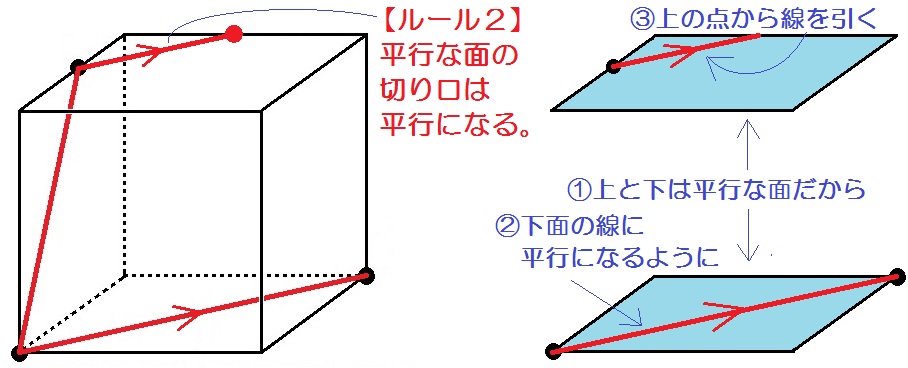
これで奥に、同じ面上の２点ができたので、またルール１に沿って結ぶだけ。

答えは以下のようになります（等脚台形という図形になる）。

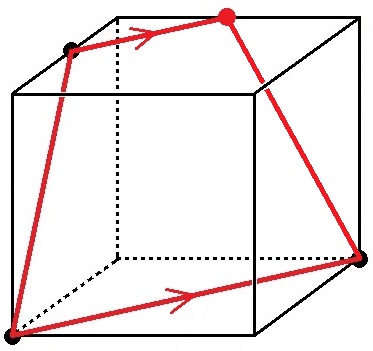
ルール１が当てはまらないときはルール２を使う。

これを、例題３でもやってみましょう。

 

五角形になる切り口

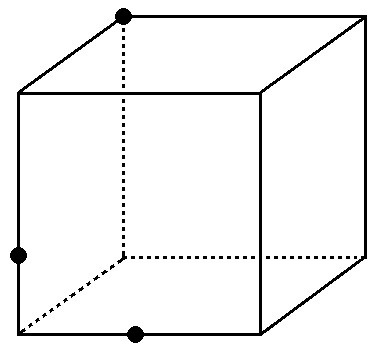
まずルール１「同じ面上の２点は結ぶ」に沿って↓

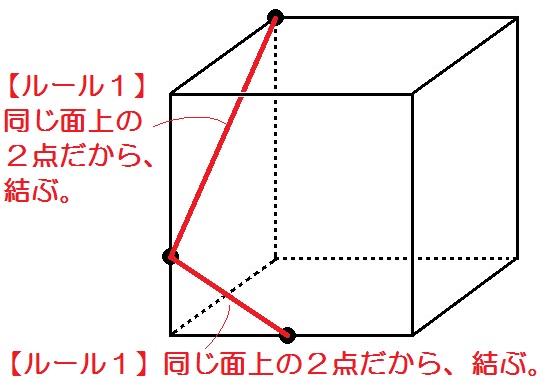
次にルール２「平行な面の切り口は平行になる」に沿って↓

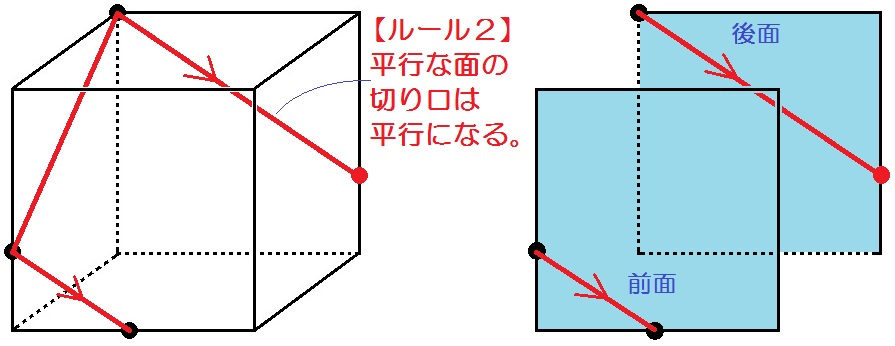
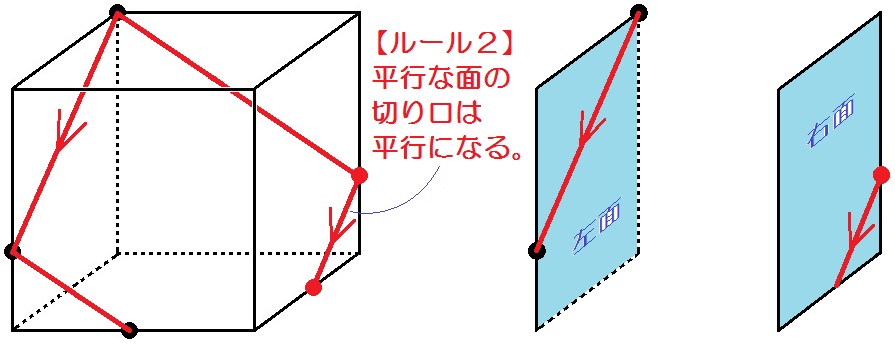
さいごはまたルール１「同じ面上の２点は結ぶ」が使える↓

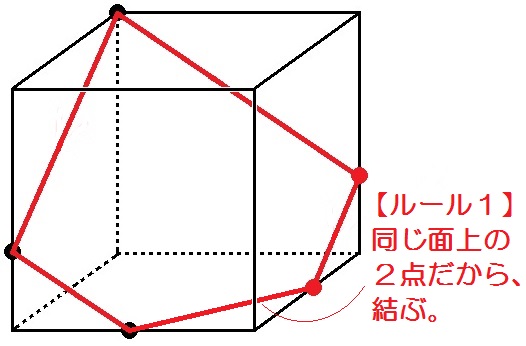
切り口の図形は五角形になります。

ではラストに、ルール１もルール２も使えない場合を見てみましょう。

 

正六角形になる切り口

この例題は、同じ面上の２点を結んだあと、ルール１はおろかルール２も使えなくなります。

だって、切り口のある面（前と左）に平行な面が、後ろと右。

そこには、点さえ無いからです。

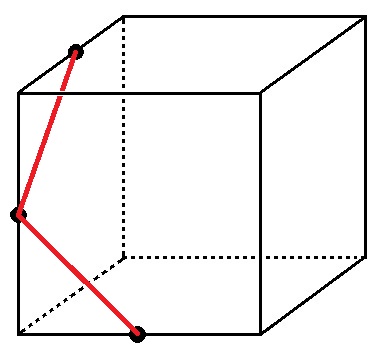
ここで初めてルール３の出番。

1. 同じ面上の２点は結ぶ
2. 平行な面の切り口は平行になる
3. 面を延ばす

つまり、立方体の面を拡張するんです↓

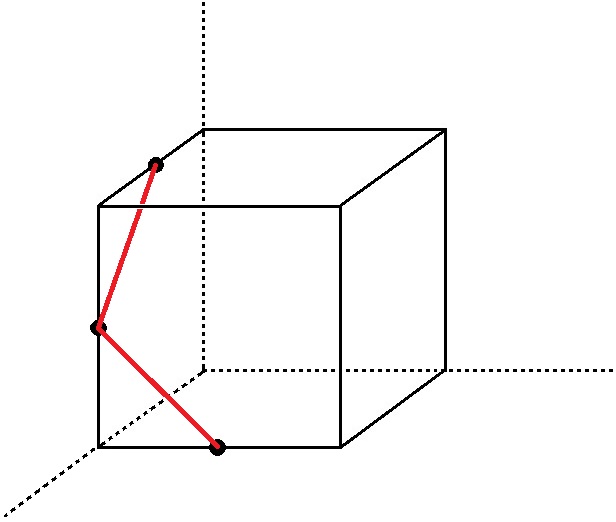
イメージとしては、部屋のすみっこにダンボールを置いたかんじ。

ダンボールの面だけじゃなく、部屋の壁や床までまるごとぶった切るかんじです。

まるごとぶった切るから、切り口の線も伸ばします。

どっちに伸ばしてもいいけど、とりあえず上に伸ばしてみましょう。

すると、後ろ面に点ができます（青い丸）↓

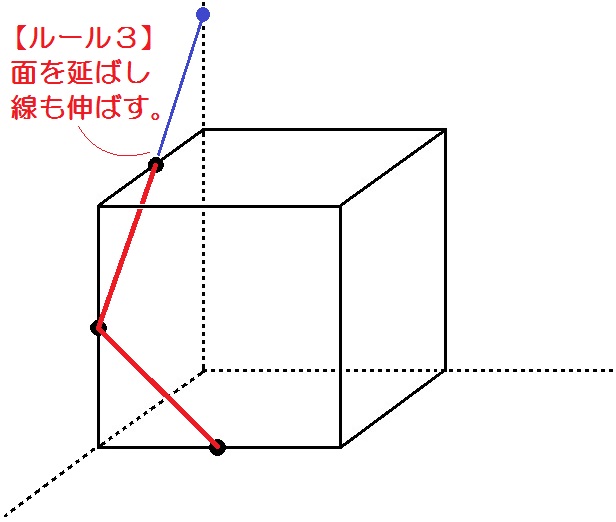
ここからはルール１とルール２だけでいける。

つまり、こんなかんじ↓

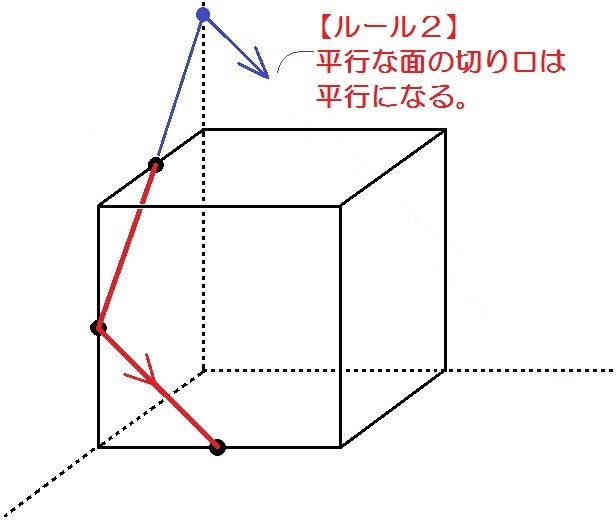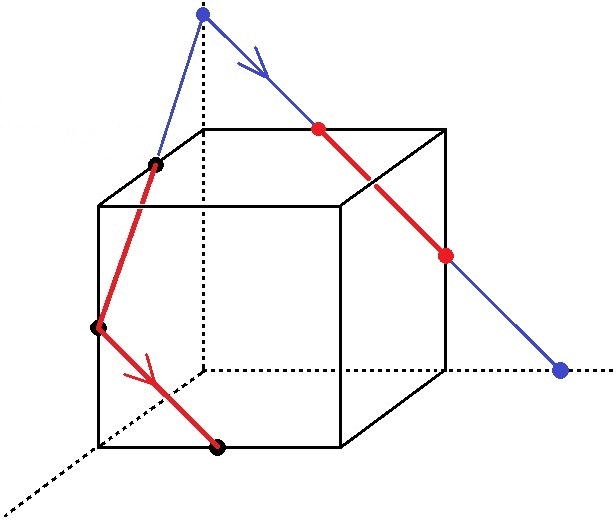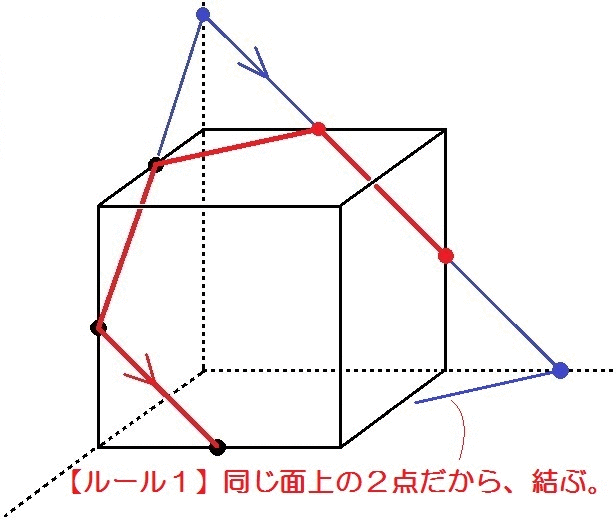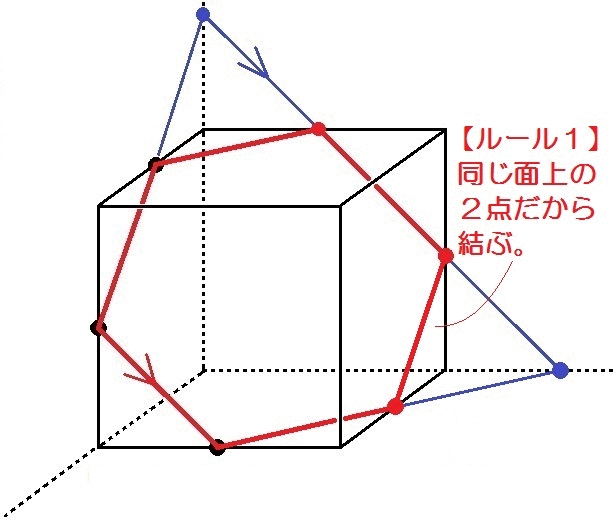
切り口の図形は正六角形になります。

＊今回は切り口を上に伸ばしましたが、もちろん下に伸ばしてもＯＫ。時間のある人はやってみてください。

以上のように、

1. 同じ面上の２点は結ぶ
2. 平行な面の切り口は平行になる
3. 面を延ばす

というルールを上から順に当てはめていく。

これが切り口の図形をかくときのコツでした。

 

練習問題

ここでネタバレをすると、以上のコツは下の２つの動画を参考にしました。

いやー、どっちもわかりやすかった。

頭の整理になるので、ぜひ視聴してみてください↓

最近はYouTubeでいろんな人が指導法を共有してくれるので勉強になります。

では、やり方がわかったら、次はできるように訓練しましょう。

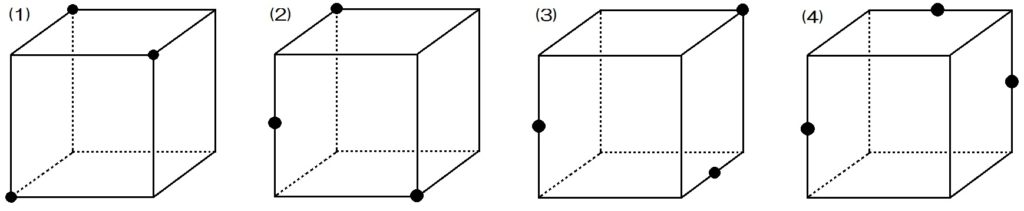
つまり練習問題です。

ノートなどに見取り図をかき写して、やってみてください。

質問はコメント欄からどうぞ。

＞次ページ：切断された立体の体積