中学数学のつまずき解消をめざすこの連載。
今回から中1「空間図形」に入ります。
この空間図形単元には、以下6つの内容があります。
- 平面と直線の位置関係(ねじれの位置など)
- いろいろな立体(正多面体、展開図など)
- 立体の見方(投影図、回転体など)
- 体積(柱・錐・球など)
- 表面積(柱・錐・球など)
- 立体の切断(切り口の図形、切断された立体の体積や表面積)
このうち前半の1~3で「わからない・できない」となる中学生。
その原因と解決方法は?
これをまずここで紹介します。
(後半4~6の解決方法については、のちの記事で)
「展開図から立体をイメージできない…」
「回転体の問題がよくわからない…」
こんな生徒にご参考ください。
空間図形が苦手になる原因

空間図形の学習に入り、まだ高校入試レベルの難問に出合ったわけでもないのに「よくわからない」となる中学生がいます。
この原因は、空間認識能力が低いことにあります。
空間図形が得意な人・苦手な人
「空間認識能力」とは、モノの形・大きさ・奥行き・方向などを3Dで正確に把握できる能力のこと。
ようするに、頭のなかで立体をちゃんと立体的にイメージできる力です。
ジュウゴの経験上、この空間認識能力が高い子は、以下のような特徴があります。
- ちいさい頃、自然のなかでよく遊んでいた
- 工作や立体パズル、積み木などでよく遊んだ
- 球技をやっている
- 3Dゲームをよくやる
- 風景を描くのが好き
こんな中学生にとって、空間図形の前半はカンタンです。
しかし、そうじゃない人、つまり空間認識能力の低い人にとっては、空間図形単元は「なんかよくイメージできない」となります。
とくに
- 球技が苦手
- 地図を見ながら移動できない
- よく転ぶほうだ
- 美術の実技の成績があまりよくない
こんな中学生は、立体を立体的にイメージするのが苦手なので、空間図形に初めからつまずいてしまうのです。
空間認識能力は鍛えられる
でもダイジョウブ。
空間認識能力は中学以降でも鍛えることができます。
中学生どころか大人でも鍛えることができて、たとえばサッカーの本田圭佑選手はこんなトレーニングをしてるみたい↓
空間認知能力を高めるトレーニング。子供には特にいいんで、毎日1、2回くらいでいいので、トライしてみてください。 pic.twitter.com/gPilOpkcZY
— KeisukeHonda(本田圭佑) (@kskgroup2017) November 8, 2018
ただこれはサッカーのトレーニングで、数学のトレーニングとはちょっと違う。
「空間図形」という数学単元ができるようになるためには、どんなトレーニングがいいのか?
以下、3つ紹介していきます。
空間図形が苦手という人は、じっさいの問題を解くまえに、この3つのトレーニングをしてみてください。
早い人なら数日間で効果を実感できるはずです。
>Amazonプライム・ビデオで「新世紀エヴァンゲリオン」を観る
解決方法=手を動かすこと!

空間図形の苦手を克服するために、有効なトレーニング。
それはじっさいに手を動かして空間認識能力を高めることです。
具体的には、
- 立体を作って、もてあそぶ
- 見取り図を、きれいに描く
- 身近なモノで、試してみる
という3つをオススメします。
1.立体を作って、もてあそぶ
まずオススメするのは、立方体・三角柱・円錐などの立体を自分で作るというもの。
たとえば立方体の展開図の問題がわからないとき、目の前に立方体があって、それを展開することができたら、かならず解けますね。
たとえば投影図の問題がわからないとき、目の前にいろいろな立体があって、それをさまざまな角度から眺めることができたら、「四角錐だ!」ってわかりますね。
だから、立体を作るんです。
この手間を惜しんで、空間図形が苦手なのに頭のなかだけで考えつづける人のなんと多いことか。
設計図(展開図)も見つけてきたんで、以下のサイトにとんで、10種類の立体の展開図をそれぞれプリントアウトしてください。
んでそれを厚紙に貼って、ハサミで切り取ります。
のりしろには、あとでまた展開するために、のりをちょっとだけ付けて組み立てましょう。
組み立てる過程も、トレーニングになります。
出来上がったら、勉強机のそばに置いておきます。
必要に応じて、さまざまにもてあそびましょう。
なお、どうしても手間をかけたくないという人は代わりにお金をかけてこちらをどうぞ↓
立体が出来上がったら、とくに
- いろんな角度から眺めてみる
- もういちど展開してみる
- 模写してみる
などをしてみるといいでしょう。
空間認識能力が鍛えられます。
立体を作って、もてあそぶ。
これが空間図形の第一のトレーニングです。
2.見取り図を、きれいに描く
第二のトレーニングは、見取り図をきれいに描くことです。
空間図形が苦手な中学生は、見取り図がおかしい。
たとえば立方体を描くとこんなかんじ↓
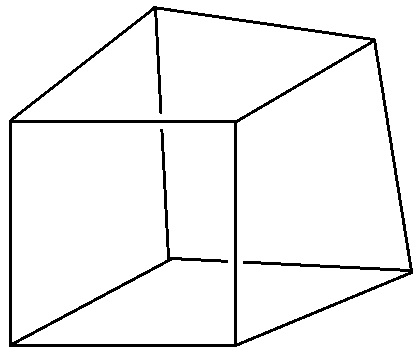
見取り図:悪い例
これでは「ねじれの位置」の問題など、できるようにはなりません。
だから見取り図をきれいに描くトレーニングをするんです。
きれいに描くコツは2つ。
- 平行な線は見取り図のうえでも平行になる
- こっちから見えない線は点線にする
たとえば、こんなかんじ↓
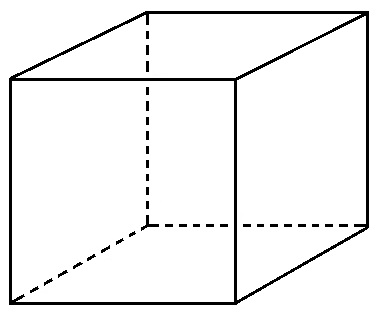
見取り図・良い例
いま、ノートとペンのある人は、この見取り図を描き写してみてください。
もちろん定規を使ってOKです。
できましたか?
では次に、定規を使わずにもういちど描き写してみてください。
できましたか?
こんなトレーニングをいろいろな立体でおこなうこと。
それだけで空間図形の出来がちがってきます。
見取り図を、きれいに描く。
これが空間図形の第二のトレーニングです。
なお、ノートはドット(点)のあるものがオススメです。
こちらなど使いやすいですよ↓
3.身近なモノで、試してみる
第三のトレーニングは、身近なモノを使って問題を再現してみることです。
たとえば、三角形の回転体の問題がわからないなら、ちいさな旗をつくって回してみる。
たとえば、直方体の切り口がイメージできないなら、豆腐を包丁で切ってみる。
「よくイメージできないな」と感じるたびに、こうした再現をしてみる姿勢。
これが大事なんです。
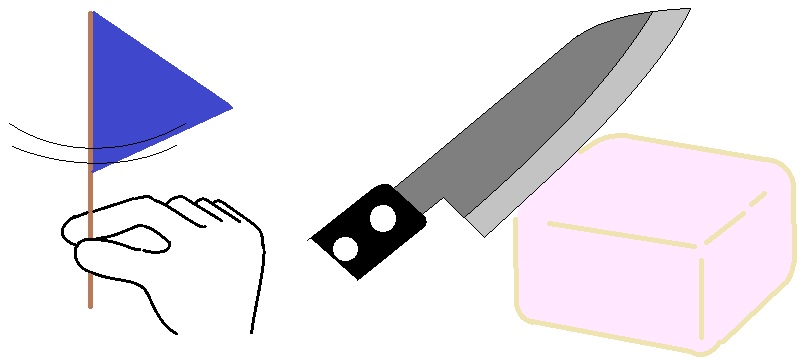
身近なモノで試してみると、いままでよくわからなかった事柄がストンと腑に落ちる、こんなことがよくあります。
以下ではその例として、「平面が1つに決まる条件」を、身近なモノを使って考えてみましょう。
>Amazonプライム・ビデオで「グッド・ドクター 名医の条件」を観る
平面が1つに決まる条件を考えてみよう

「こういう条件に当てはまる平面は1つしかない」。
これが、平面が1つに決まる条件のことです。
ようするに、下敷きや板を載せたときにグラグラしない場合ってどういうとき?ってのを考える問題です。
点で平面が決まる場合
では、以下のモノを用意してください。
- 下敷き
- 棒
- ビー玉
(下敷きの代わりにうすい板、棒の代わりに鉛筆やペン、ビー玉の代わりにアメ玉や消しゴムの切れはしでもOKです。)
まず、ビー玉だけで下敷きがグラグラしないよう支えるには、どうしたらいいでしょう?
1個だけじゃダメ。2個でもダメ。3個…で支えることができますね。
だから点だけで平面を1つに決めるには、最低3点が必要なんです。
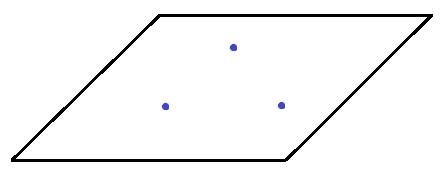
ただ、ビー玉3個でも下敷きがグラグラする場合があります。
いろいろ試してみてください。
わかりました?
そう、3個が一直線上に並んだときです。
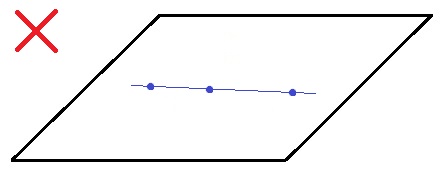
以上の実験から、平面が1つに決まる条件がまずひとつわかりました。
「一直線上にない3点」というのが、それです。
直線で平面が決まる場合
つぎに、棒だけで下敷きがグラグラしないように支えてみましょう。
棒1本じゃダメ。棒2本…でいけますね。
だから直線だけで平面を1つに決めるには、最低2本が必要なんです。
ただ、棒2本でも下敷きを支えられない場合があります。
たとえば1本は寝てるけどもう1本は立ってる場合とか。
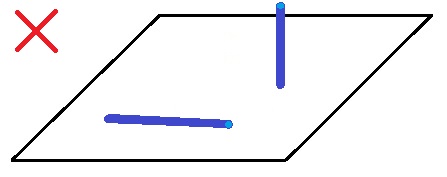
だから下敷きがグラグラしないためには、2本とも机の上に寝ていないといけない。
ところで、棒には両端がありますが、直線って両方向にかぎりなく伸びたものでしたね。
いま、目の前にある棒2本それぞれ、両方向にかぎりなく伸びたとイメージしてください。
どっかで交わりますね。
あるいは平行のままですね。
以上から、平面が1つに決まる条件のふたつめとみっつめがわかりました。
「交わる2直線」
「平行な2直線」
というのが、それです。
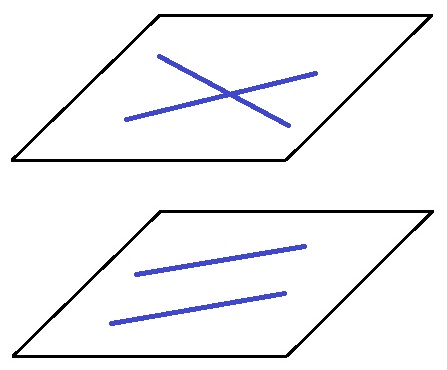
点と直線で平面が決まる場合
最後に、ビー玉と棒の両方を使って、下敷きがグラグラしないように支えてみましょう。
そう、ビー玉1個、棒1本あれば支えられます。
だから点と直線で平面を1つに決めるには、1つずつあれば十分なんです。
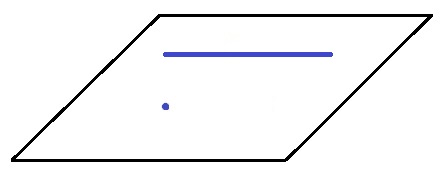
ただやっぱり、下敷きがグラグラする場合もあります。
試して、わかりましたか?
棒の延長線上にビー玉があるときです。
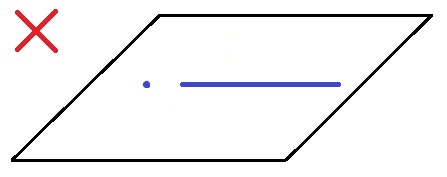
以上から、平面が1つに決まる条件のよっつめがわかりました。
「1つの直線と、その直線上にない1点」です。
こうして、平面が1つに決まる条件4つ
- 一直線上にない3点
- 交わる2直線
- 平行な2直線
- 1つの直線と、その直線上にない1点
がわかりました。
身近なモノで試してみると、イメージがわきやすい。
このことを感じてもらえたでしょうか。
まとめ

空間図形の前半でもうつまずく原因は、空間認識能力が低いこと。
でも、手を動かすことで鍛えられる。
具体的には
- 立体を作って、もてあそぶ
- 見取り図を、きれいに描く
- 身近なモノで、試してみる
というトレーニングをする。
空間図形単元の最初「平面が1つに決まる条件」も、こうしたトレーニングを取り入れればイメージできる。
では次回から、じっさいに問題を解くときのコツを解説していきます。
ただ、ここで紹介した3つのトレーニングは超重要。
土台となる空間認識能力を鍛えることを忘れずに。
NEXT→中学数学「空間図形」② 位置関係・展開図・回転体のコツ
≪「空間図形」の記事一覧≫
- 空間図形① 苦手になる原因と解決方法
- 空間図形② 位置関係・展開図・回転体のコツ
- 空間図形③ 体積のコツ
- 空間図形④ 表面積のコツ
- 空間図形⑤ 立体の切断問題のコツ








コメント
紙の上(平面)に書かれた図形を見るだけでなく、
手を動かす(空間)のが大事、
というわけですね。