中１数学「空間図形」の２回目です。
今回は空間図形単元の前半で、多くの中学生が「苦手だー！」ってなる問題を解説します。
つまり
- 「ねじれの位置」の見つけ方
- 展開図の応用問題
- 複雑な図形の回転体
という３つ。
それぞれのコツを紹介するので、おぼえて使ってください。
ただ前回も言いましたが、基本は空間認識能力を鍛えること。
コツだけに頼ってたら応用力が向上しないんで、前回の記事で紹介したトレーニングは続けてくださいね。
[連載記事一覧]
- 空間図形① 苦手になる原因と解決方法
- 空間図形② 位置関係・展開図・回転体のコツ
- 空間図形③ 体積のコツ
- 空間図形④ 表面積のコツ
- 空間図形⑤ 立体の切断問題のコツ
位置関係のコツ
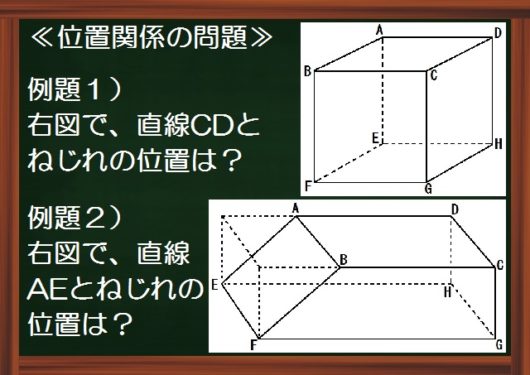
位置関係の問題でむずかしいのは、直線と直線の位置、とくに「ねじれの位置」の見分け方です。＊直線と平面、平面と平面の位置関係はカンタンです。できないって人はペンと下敷きを用意してもてあそんでください。
そこで、以下のコツが有効です。
「交わる」と「平行」に×していって、残りが「ねじれの位置」。
「交わる」と「平行」に×する
例題１）下図の立方体で、直線CDとねじれの位置にある直線をすべて答えよ。
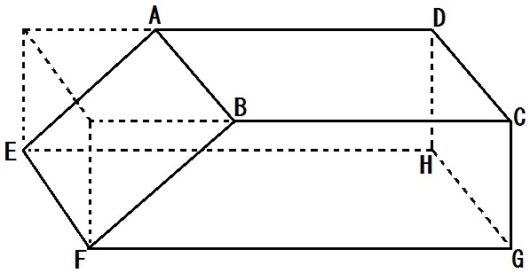
たとえばこの例題１。
まず直線CDと「交わる」直線にぜんぶ×をします。
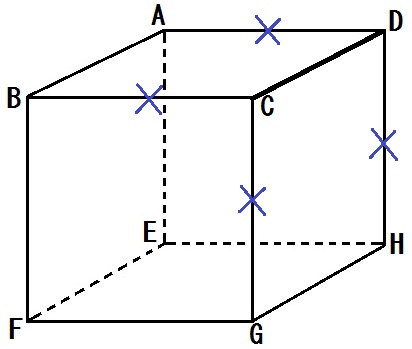
つぎに、直線CDと「平行」な直線にも×をします。
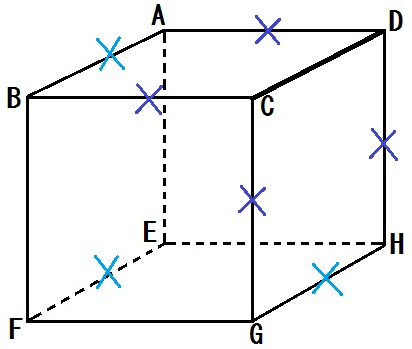
そうしたら、おのずと、×のついてない直線が「ねじれの位置」になります。
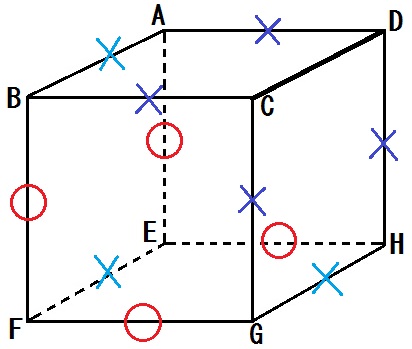
答えは
直線AE、直線BF、直線EH、直線FG
の４本とわかる。
このように、ねじれの位置の問題は消去法でやっつけられるのです。
[関連記事]
例題２）下の図は、直方体から三角柱を切り取った立体である。直線AEとねじれの位置にある直線をすべて答えよ。
もう１問やってみましょう。
交わる直線と平行な直線に×をしていって、残りがねじれの位置です。
ただ例題２の注意点は、直線とは両方向にかぎりなく伸びたものってトコロ。
…。
……。
できましたか？
答えは
直線BC、直線FG、直線DC、直線HG、直線CG
の５本です。
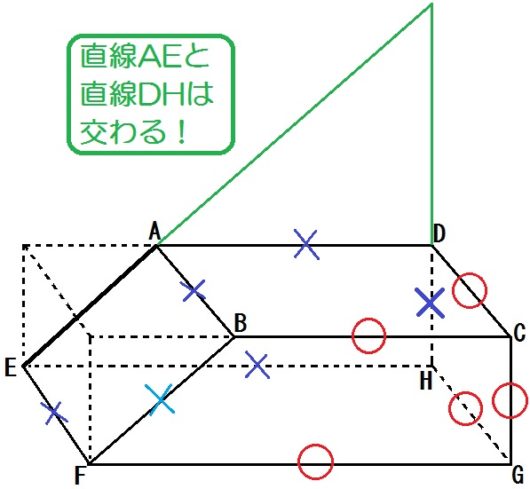
AEとDHは延長したら交わるってトコロに注意しましょう。
そこだけ気を付ければ、あとはカンタンですね。
ねじれの位置は「交わる」＆「平行」にバツをつけて消去法。
このコツですぐに解けます。
練習問題
では、練習問題を用意しました。
ぜひチャレンジしてみてください。
画面上の図形には×をつけられないので、見取り図を書き写してやってみるといいでしょう。
質問はコメント欄からどうぞ。
あ、数えもれがないように気をつけるってトコロもポイントですよ。
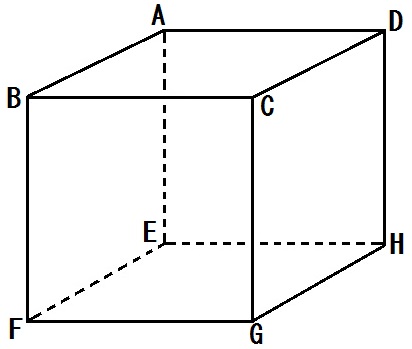
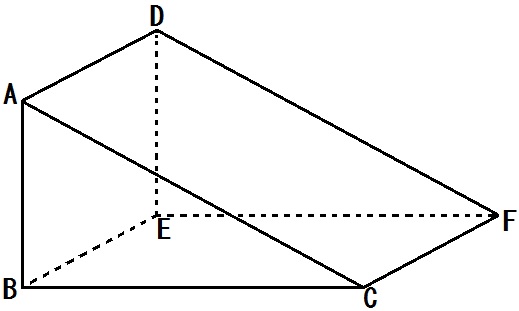
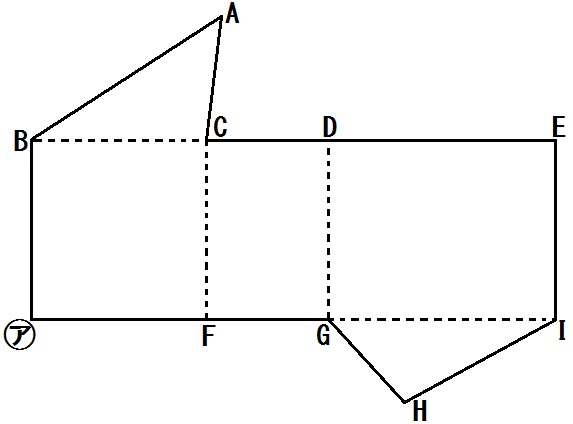
下の図において、次の関係にある直線をそれぞれ全て答えよ。
問題１）直線BCとねじれの位置にある直線
問題２）直線ACとねじれの位置にある直線
問１）直線AD、直線DE、直線DF
問２）直線BE、直線DE、直線EF
＞Amazonプライム・ビデオ「四角い恋愛関係 (字幕版)」
展開図のコツ
展開図でむずかしいのは、見取り図と展開図との対応関係を答える問題。
つまり
- 対応する頂点を答えたり
- サイコロの目を展開図に書きこんだり
- 立体にひっかけたヒモを展開図に書き加えたり
といった問題です。
こーゆー問題では、展開図に頂点を順に書きこんでいくというコツを使うといいでしょう。
頂点を順に書きこんでいく
例題３）図２は、図１の正八面体の展開図である。点アに対応する頂点を答えなさい。
2019年度 沖縄県公立高校入試問題 9-1
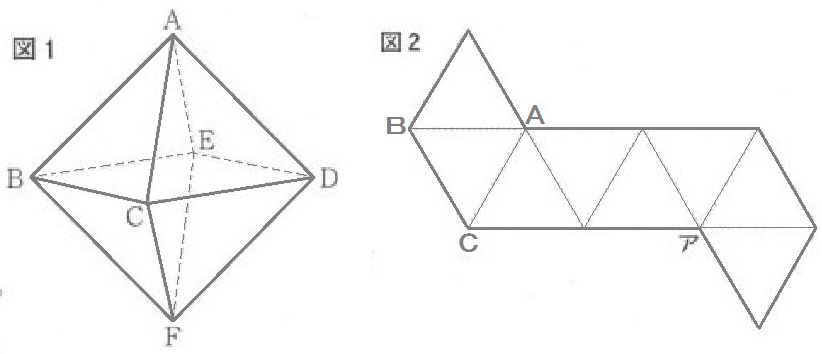
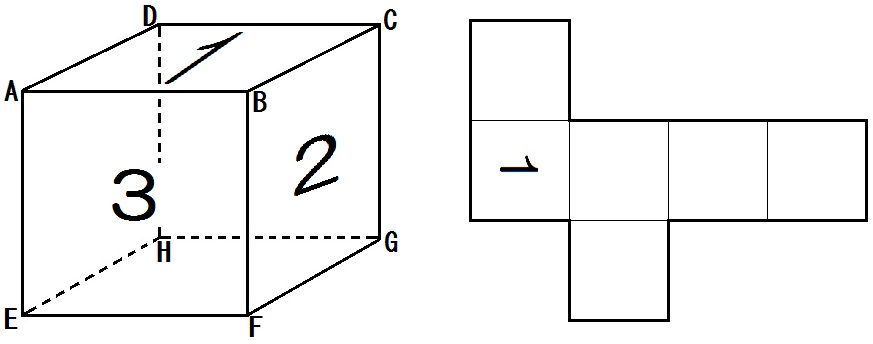
たとえば例題３。
わかる人は頭の中でイメージできますが、苦手な人はまず、展開図に頂点を順序よく書きこんでいくこと。
つまりこんなかんじです↓
「図2の展開図において、△ABCを基準にして、
- 上の三角形：ABを辺にもつのは、△ABCの他に……△ABE。
→だから残りの頂点は E だ！ - 右の三角形：ACを辺にもつのは、△ABCの他に……△ACD。
→だから残りの頂点は D だ！」
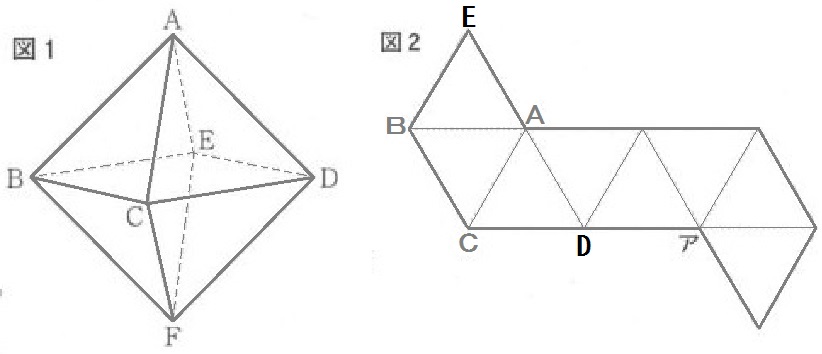
このようにして、見取り図を確認しながら、頂点を順にうめていくんです。
この次はADを辺にもつ三角形ですね。
△ACDの他に？そう、△ADE。
その次はDEを辺にもつ三角形。
△ADEの他に？そう、△DEF。
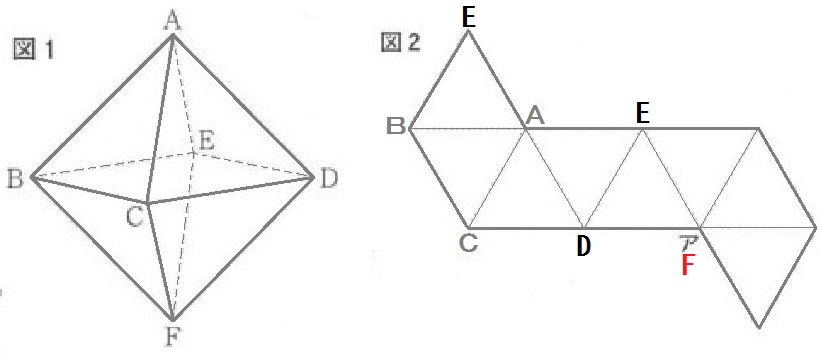
こうして答えは「F」と出ます。
[関連記事]
例題４）図１のように、正六面体の辺の中点を結んで六角形PQRSTUをつくった。図２の展開図に、六角形の辺を書き加えよ。
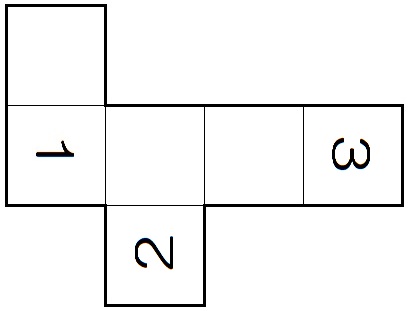
じゃ、ヒモをひっかけるような問題もやってみましょう。
すぐできなければ、まず展開図に頂点を順に書きこんでいきます。
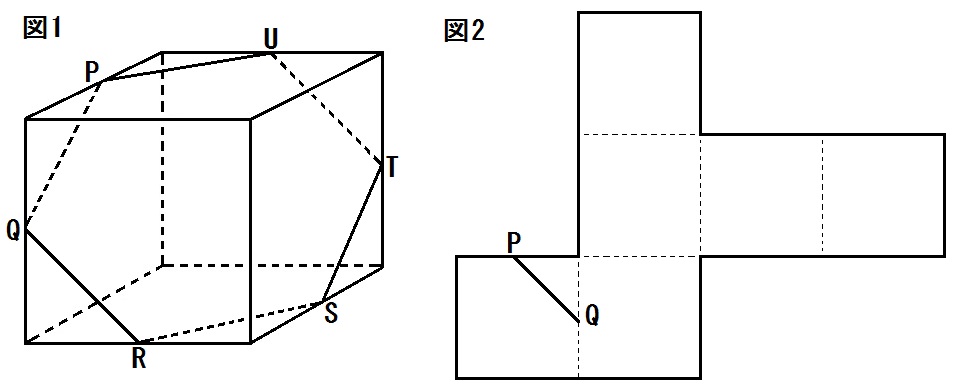
この例題４には頂点のアルファベットがないので、自分で書いちゃいましょう。
たとえばこんなかんじ↓
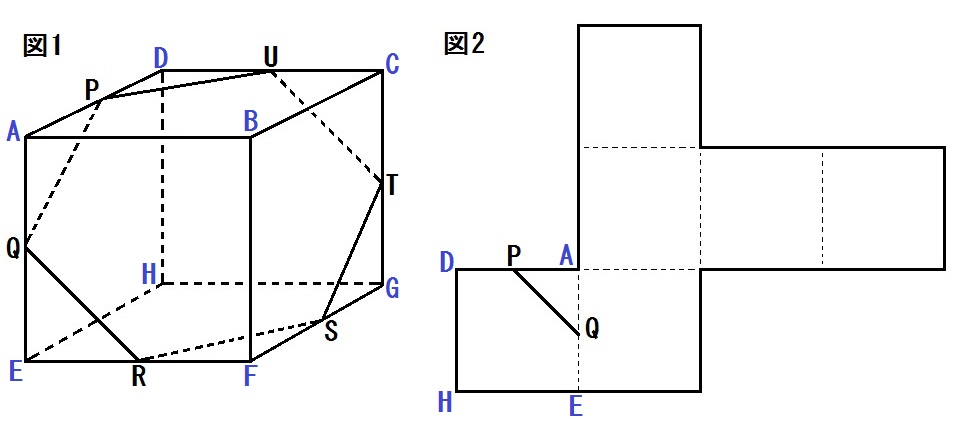
すると、辺PQがあるのは面DHEAだとわかります。
次にその右の正方形。
AEを左にもつのは？そう、面AEFB。
次は上の正方形。
ABを下にもつのは？そう、面DABC。
以下、順々に書きこんでいって、頂点がすべてそろいます。
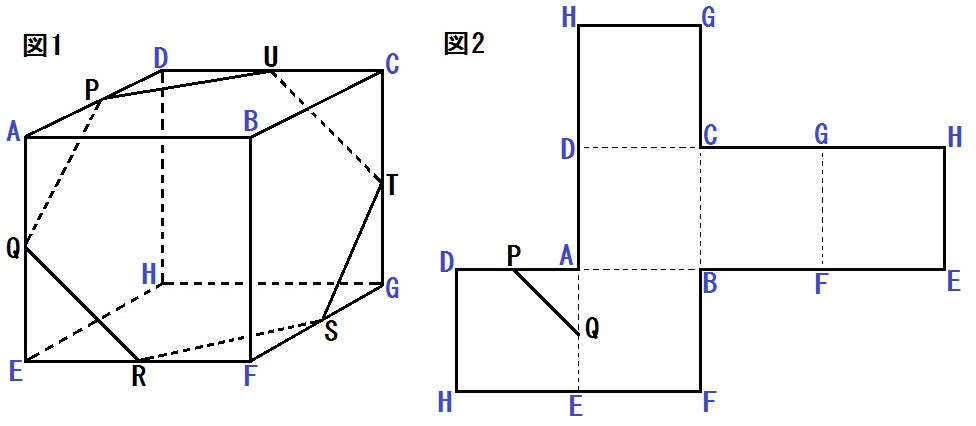
ここまで書きこめば、あとはカンタン。
辺QRがある面はどれ？
辺RSがある面はどれ？
と、ひとつひとつ平面で考えればいい。
答えは以下のとおり。
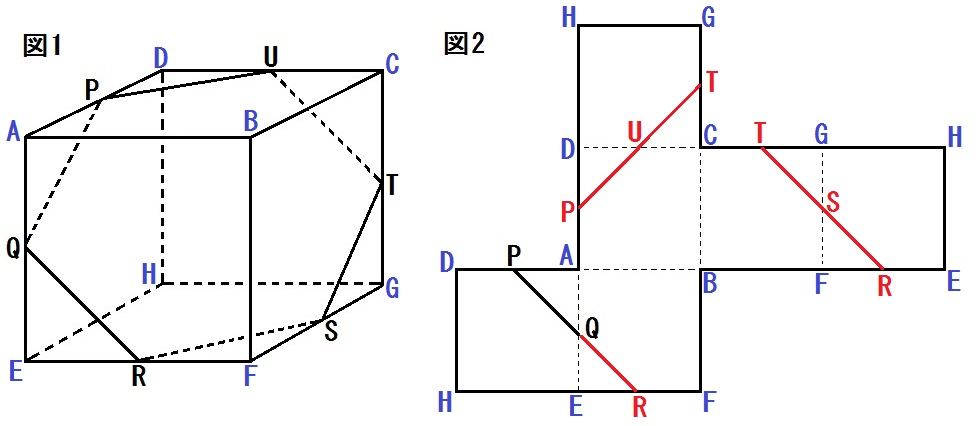
以上のように、展開図の問題がむずかしければ、まず頂点を順に書きこんでいくこと。
そうすれば一見複雑な応用問題でも、できるようになります。
練習問題
ただ、このコツはあくまで、展開図問題ができないってときに限ります。
理想は頂点など書かなくても答えられること。
つまり頭のなかで立体がパラパラと展開したり、展開図がカチッカチッと組み立てていったりできるようになること。
だってそのほうが早く答えられるから。
よって、前回の記事で書いた３つのトレーニングで空間認識能力を鍛えることは忘れずに。
では、練習問題です。
（問題４がむずかしいなら、自分で見取り図をかいて展開図と対応させるといい）
問題３）下の図において、展開図に数字の２と３を、向きも考えて記入せよ。
問題４）下の展開図をもとに立体をつくるとき、アと重なる点をA～Iから選べ。
問３）下図 問４）I
＞Amazonプライム・ビデオ「イマジン/ジョン・レノン(字幕版)」
回転体のコツ
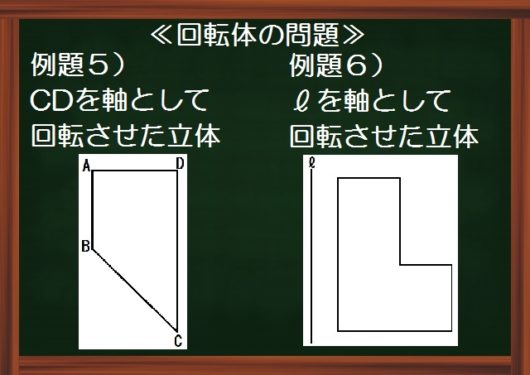
回転体の問題でむずかしいのは、複雑な図形や、回転軸から離れている図形をまわすとき。
そこで、見取り図がちゃんとかけないって人は、まず左右対称な図を描くというコツを使うといいでしょう。
左右対称な図を描く
例題５）下図の台形ABCDを、直線CDを回転の軸として１回転させてできる立体の見取り図をかけ。
2019年度 京都府公立高校入試問題(中期) 3-2改
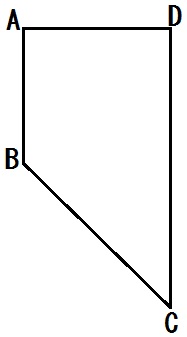
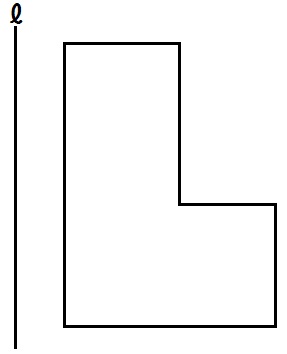
たとえばこの例題５。
イメージできる人はいいですが、苦手な人は以下の手順で描くといい。
- 問題図に左右対称な図形を描き
- 対応する頂点どうしを楕円でグルッと結んで
- それを下絵にして見取り図をかく
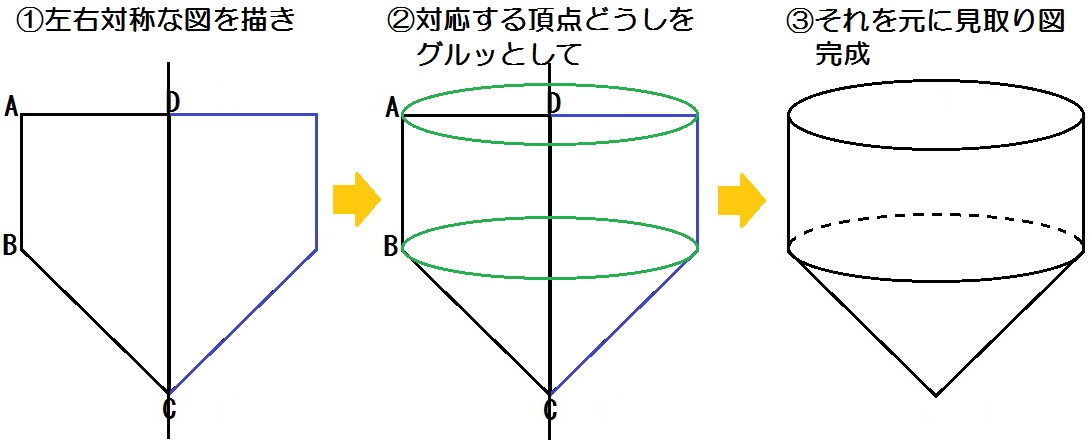
注意点として
- 回転の軸から離れている頂点だけをグルッとする
- 見取り図をかくとき、こちらから見えない線は点線にする
- 辺ADとかは見取り図にかかない
という３点があります。
[関連記事]
例題６）下の図形を、直線ℓを回転の軸として１回転させてできる立体の見取り図をかけ。
では、回転の軸から離れている問題もやってみましょう。
まず左右対称な図形を描き、対応する頂点どうしを楕円でグルッと結びます。
６コの楕円ができますね。
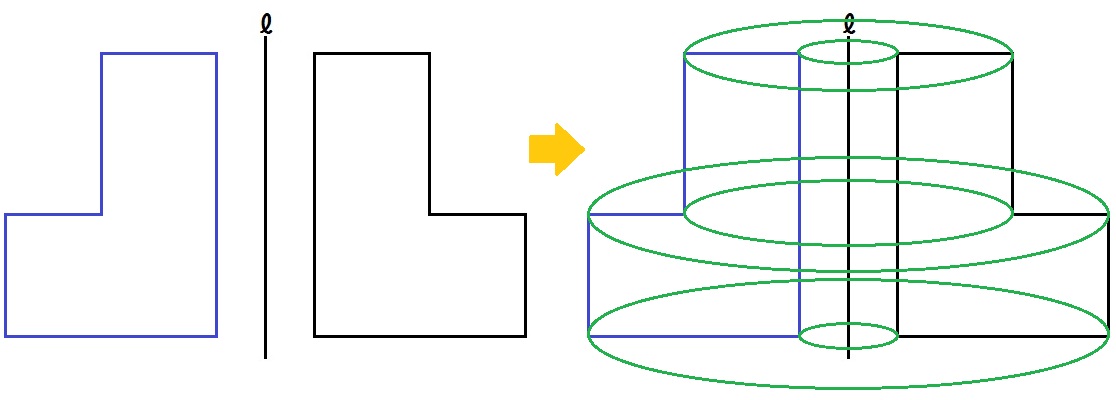
これを元に、見取り図をかいていく。
とくにどこが見えてどこが見えないかに注意しましょう。
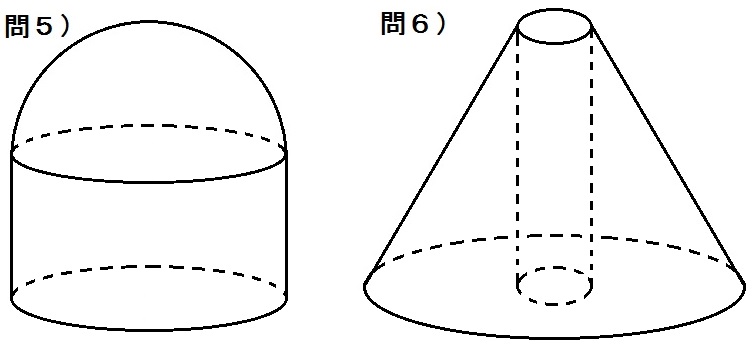
答えは↓
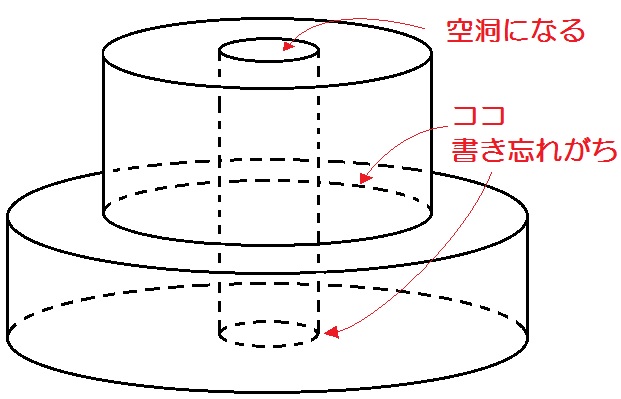
ガムテープを２つ重ねたような立体になります。
回転軸から離れた図形を回転させると空洞ができるってこともわかりますね。
以上のように、回転体の問題が苦手ならまず左右対称な図を描いて頂点どうしをグルッと結ぶといいでしょう。
練習問題
ただ、回転体の問題もやはり空間認識能力が基本。
じっさいの円錐やトイレットペーパーを観察したり、見取り図をきれいに描いてきた経験が必要です。
何度もいいますが、前回の記事で書いた３つのトレーニング、怠らないで。
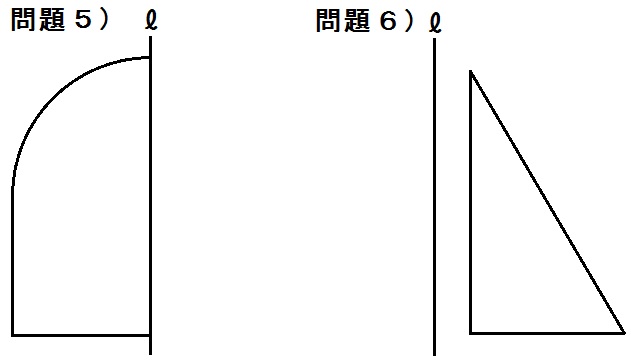
では、さいごの練習問題です。
下の図形を、直線ℓを回転の軸として１回転させてできる立体の見取り図をかけ。
解答↓
＊なお、この回転体問題は体積や表面積の問題としてもよく出題されます。
くわしくは以下の記事を参照。
まとめ
○ねじれの位置を見つけるのが苦手なら…
→「交わる」と「平行」に×していく（消去法）。
○展開図と立体の対応問題が苦手なら…
→展開図に頂点を順に書きこんでいく。
○ややこしい回転体の問題が苦手なら…
→まず左右対称な図を描き、頂点どうしをグルッと結ぶ。
＊ただし基本は空間認識能力を鍛えること。
以上！
[関連記事]
次回は体積のコツをお伝えします。
とくに
- 柱の高さを求める問題
- 組み合わせた立体の体積
- 水を入れる問題
などを解説していく予定です。
NEXT→中学数学「空間図形」③ 体積のコツ
[連載記事一覧]
- 空間図形① 苦手になる原因と解決方法
- 空間図形② 位置関係・展開図・回転体のコツ
- 空間図形③ 体積のコツ
- 空間図形④ 表面積のコツ
- 空間図形⑤ 立体の切断問題のコツ
コメント
展開図は、立方体でいえば、
９０°を為す２辺同士は重なる、
その隣の２辺同士も重なる、
ということを知っていると、
問題４なんかは楽に解けるかと思います。
（答えがＨになっていますが、Ｉでは？）
問４の解答、修正しました。
ご指摘ありがとうございます、失礼しました。