中1数学 1次方程式の文章問題。
9回目は「図形の問題」における解き方のコツをお伝えします。
図形問題というと証明や相似、三平方の定理などがすぐ思い浮かびますが、じつは方程式で解く図形問題というのも、定期テストや受験でよく出題されます。
また、高校受験でよくみかけるのが点の移動する問題、つまり動点の問題ですが、これ、1次関数の問題としてだけでなく、ときおり1次方程式の問題としても出されることがあります。
つまり高校入試とは、あらゆる分野を総合した力が求められるテストなんです。
よって、中1の頃から「代数」「関数」「図形」「統計」という数学4分野を横断的に勉強していくと、中3で困らなくて済みます。
そこで今回は1次方程式 文章題の最後として、図形問題を扱うわけです。
方程式分野だけでなく、関数にも図形にも通じる解き方のコツを、4パターンに分けて紹介します。
ぜひここで身につけて使っていってください。
図形問題の基本

まずは図形問題の基本から。
図形の問題では「どんな図かイメージする」というのがとても重要です。
よって基本的なコツとしてまず2つ。
- 図がなかったら自分できれいに描く
- \(x\) も使って長さをぜんぶ書きこむ
それぞれ順をおって説明します。
解き方のコツ
例1)下底の長さが上底の長さより2cm長い台形がある。この台形の高さは7cm、また面積は28㎠である。この台形の上底の長さを求めよ。
この例題は「上底の長さ」という数量を求める問題です。
よってある数量を求める問題は方程式で解く、というのが数学の定石になります。
だから一行目には「上底の長さを \(x\) cmとする」等と書きます。
次に方程式をつくりますが、この例題、図がありません。
だから自分できれいに描くんです。問題用紙の余白や、ノートなどに。
ここで「きれいに描く」ができない生徒は注意が必要です。

このように描いちゃう中学生。けっこういますね。
こんな生徒はたいてい、反比例のグラフや空間図形の見取り図もうまく描けません。
んでそのまま学年が進んで、中2「証明」や中3「2次関数」「相似」で苦労することになります。中2「確率」の樹形図もそうです。
頭のなかを整理するためにわかりやすい図を描いてイメージを助ける。
このことの重要性を知らないまま数学嫌いになった人がどれだけいたか。
なので、ジュウゴはちょっと時間がかかってもここで「イラスト講座」を持ちます。
中学生ひとりひとりがわかりやすい図を描けるまで、根気強く何度も修正させ、じょうずな図ができたらしっかり誉めます。
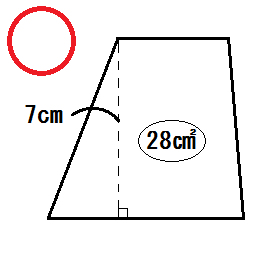
ここまでできたら、次はもうひとつのコツ。この図の中でまだ書かれていない長さを \(x\) も使って書きこんでいくんです。
いま上底の長さを \(x\) cm としました。
また下底の長さは上底より2cm 長い。
よって↓
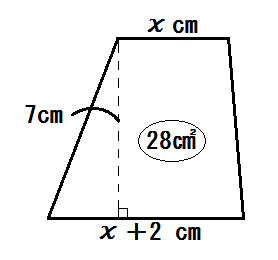
これで方程式をつくる準備が完了です。
台形の面積は28\(cm^2\) 。
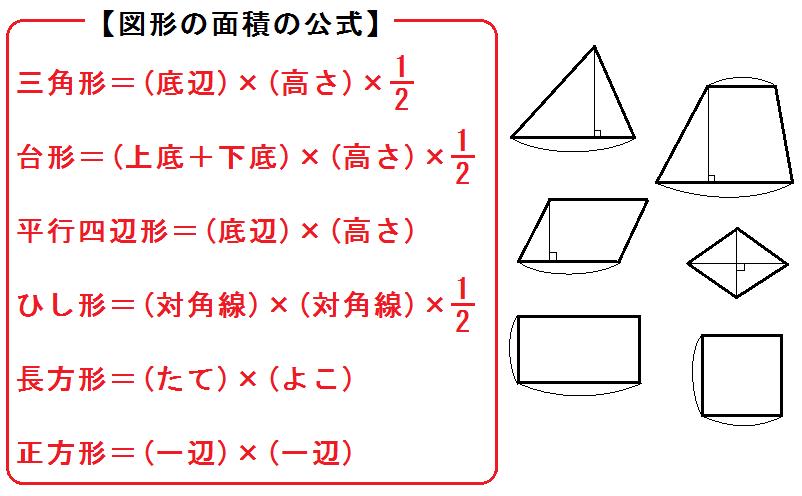
また台形の面積を求める公式は
$$ \mbox{(上底+下底)} \times \mbox{(高さ)} \times \frac{1}{2} $$
でしたね。
(なおここで各図形の面積の公式を生徒が忘れているようなら、公式一覧を書いて写させるといいでしょう。ちなみに三角形・台形・ひし形の公式を「÷2」で覚えている生徒にはここで「\( \times \frac{1}{2}\)」と変更させましょう。わりきれない場合もあるから。)
よって、方程式とその後の解法例は以下のとおり。
\begin{eqnarray} \lbrace x+(x+2) \rbrace \times7 \times \frac{1}{2} &=& 28 \\ (x+x+2) \times7 &=& 56 \\ 2x+2 &=& 8 \\ 2x &=& 8-2 \\ 2x &=& 6 \\ x &=& 3 \end{eqnarray}
答.3cm
以上のように、
図がなかったら自分できれいな図を描く
\(x\) も使って長さをぜんぶ書きこむ
これが図形問題の基本です。
練習問題
なお、以上2つのコツは方程式にかぎらず、どんな図形問題にも応用できます。
とくに「きれいな図を描く」をおぼえておくと受験でトクすることが多い。
「相似問題わからなかったけど、文章どおりにものすごくきれいに描いたら見た目で合ってた」。「図形と方程式も、ベクトルも、複素数平面も、図でなんとなく長さを答えたら正解だった」。
毎年こんな中3、高3がいます。
できるだけ文章に沿って、例題1なら下底を上底より2cm長いようにして、正確にきれいに描く。
これがフリーハンドでできるようになると、それだけで強力な武器になりますよ。
それでは、練習問題です。
解答は末尾に記載、質問はコメント欄からどうぞ。
問1)底辺が12cmの三角形がある。この三角形を底辺はそのままで、高さだけ2倍してさらに5cm長くすると、できた三角形の面積はもとの三角形の面積より54㎠大きくなった。もとの三角形の高さを求めよ。
答.4cm
周の長さが与えられた問題

次に、長方形で周の長さがわかっている問題。
ここで使える解き方のコツは、これです。
(たて)+(よこ)=周の長さの半分
解き方のコツ
長方形で周の長さというのは
(たて)+(よこ)+(たて)+(よこ)=周の長さ
です。だから、
(たて)+(よこ)=周の長さの半分
になるんですね。

このコツを使って例題2を一気に解くと、以下のようになります。
例2)横の長さが縦の長さの5倍である長方形があって、周の長さは84cmである。この長方形の、縦の長さと横の長さをそれぞれ求めよ。
解)縦の長さを \(x\) cm とする。
横の長さは \(5x\) cmと表せる。
\begin{eqnarray} x+5x &=& \frac{84}{2} \\ 6x &=& 42 \\ x &=& 7 \end{eqnarray}
また \(5 \times7 =35\)
答.縦7cm、横35cm
以上のように、長方形で周の長さが与えられている問題では、
(たて)+(よこ)=周の長さの半分
この関係式をつかって方程式をつくる。
これが解き方のコツです。
練習問題
ちなみに例題2で「縦の長さ」のほうを \(x\) としたのはなぜか?
過去記事で解説しましたね。
「BはAより~」「BはAの~倍」だったらAのほうを \(x\) とすると。
忘れた人は以下の記事をみて復習してください。

また例題2においても、最初に解説したコツ2つ
- 図がなかったら自分できれいに描く
- \(x\) も使って長さをぜんぶ書きこむ
を活かしています。とくに後者のコツは次に述べる「円をふくむ問題」でも重宝します。
それでは練習問題をどうぞ。
問2)縦の長さが横の長さの半分で、周の長さが66cmである長方形の、面積を求めよ。
答.242㎠
>Amazonプライム・ビデオで「タイタンの戦い(2010)」を観る
円をふくむ問題
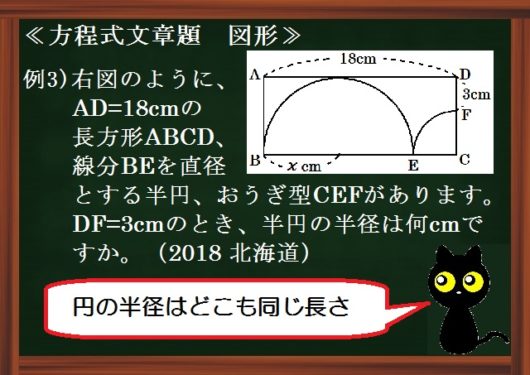
3つめはこの例題のように、円や円の一部をふくむ図形問題。
ここで新たに使う解き方のコツは
円の半径はどこでも同じ長さ
という事実です。
解き方のコツ
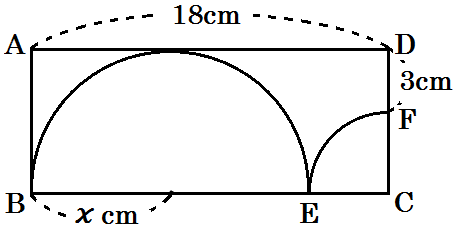
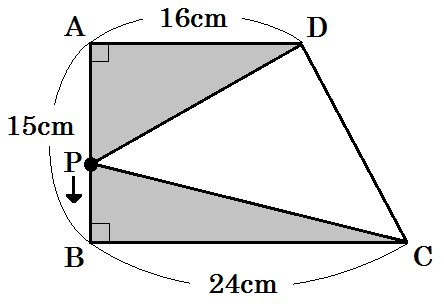
例3)下図のように、AD=18cmの長方形ABCD、線分BEを直径とする半円、おうぎ型CEFがあります。(点Eは辺BC上に、点Fは辺CD上にあり、半円は辺ADに接しています。)DF=3cmのとき、半円の半径は何cmですか。(2018 北海道)
まずは求めるもの、つまり「半円の半径を \(x\) cm」としときます。
さて、当たり前のことですが「円の半径はどこでも同じ長さ」です。
これ、意外と中学生も、高校生でさえ、気づかないことがある。
円の問題が出てきたら「半径はどこでも同じ」という事実をそのつど思い出すようにしましょう。
すると、下のように長さを書き加えられます。
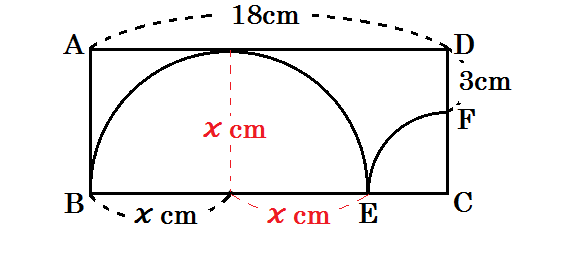
よって、長方形の縦の長さも \(x\) cm とわかる。
すると、CFの長さは \(x-3\) cm と表せることもわかる。
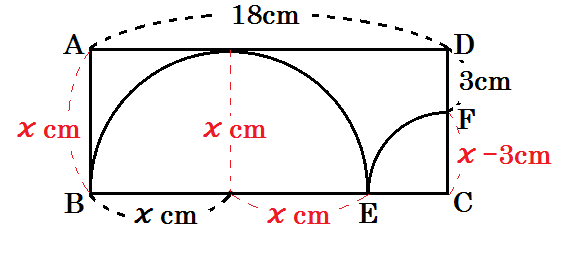
右下のおうぎ形CEFも円の一部です。
ということは、やっぱり半径はどこでも同じだから、CF=CE 。
だからCEの長さも \(x-3\) cm と表せる。
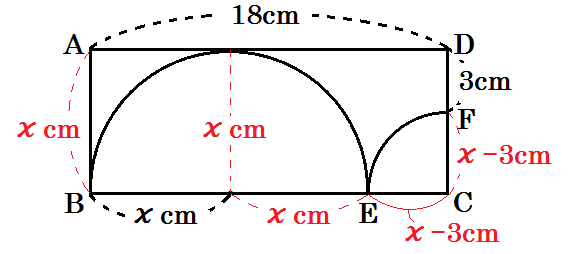
これで長方形のまわりぜんぶ、長さを表しましたね。
あとはどこかの関係で方程式をつくるだけです。
気付きました?そう、横の長さ。
上は \(18\) cm。
下は \(x\) cmと \(x\) cmと \(x-3\) cm。
よって、方程式とその後の解法は以下のとおり。
\begin{eqnarray} x+x+(x-3) &=& 18 \\ x+x+x-3 &=& 18 \\ x+x+x &=& 18+3 \\ 3x &=& 21 \\ x &=& 7 \end{eqnarray}
答.7cm
以上のように、円をふくむ図形問題では
円の半径はどこでも同じ長さ
この事実を思い出すのが、解き方のコツになります。
練習問題
ちなみに例題3では、最初に解説したコツの2つめ
- \(x\) も使って長さをぜんぶ書きこむ
これをフル活用しました。
このように、どう方程式をつくっていいかわからない図形問題でも、とりあえず表せるかぎりの長さをどんどん表していく。
そうすれば「あ!ここで等式が立つ!」と気づくことが多々あります。
とくに放物線と直線が交わっていたり、複雑な相似問題だったり、立体中に球が入っている問題だったり…。
このような受験でよく出題される難問に、とっても有効です。
- 円の半径はどこでも同じ長さ
- 表せる長さはぜんぶ書きこむ
こうしたコツを使って、以下の練習問題もチャレンジしてみてください。
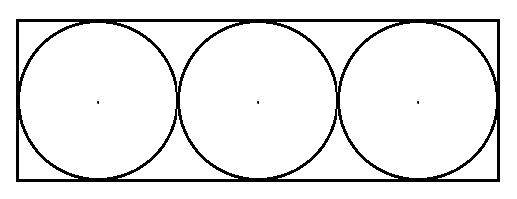
問3)下図のように、同じ大きさの円3つが長方形にちょうど収まっている。長方形の周の長さが96cmのとき、円の半径を求めよ。
答.6cm
>Amazonプライム・ビデオで「アリータ:バトル・エンジェル (字幕版)」を観る
点が移動する問題

最後に、点が移動する問題、いわゆる「動点の問題」の解き方について解説します。
動点問題は方程式の文章題だけでなく、比例・1次関数・2次関数の問題としてもよく高校受験で出題されますが、どんな場合にも当てはまるコツがあります。
それは、まず点の通った長さを \(x\) で表すこと。
そして、残りの長さを書きこむ際には辺をまっすぐにして考えること。
具体的にやってみましょう。
解き方のコツ
例4)下図のように、1辺が4cmの正方形ABCDの周上を、点PはAを出発し、毎秒1cmの速さでB,Cを通ってDまで移動する。点Pが辺CD上にあり、四角形ABCPの面積が10㎠となるのは、点PがAを出発してから何秒後か。(2018 徳島 改)
「四角形ABCPの面積が10㎠となるのは、点PがAを出発してから \(x\) 秒後とする」。
とりあえずは、求めるものをこうして \(x\) でおきます。
次に方程式を立てるために、まず点Pの通った長さを \(x\) で表します。
そのためには文章をよく読んで、点Pの通り道をイメージしましょう。
時間が経つごとに、Pはどう動きますか?
こんなかんじですね↓
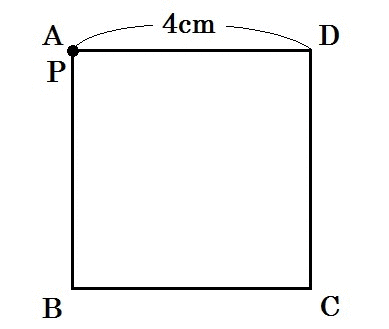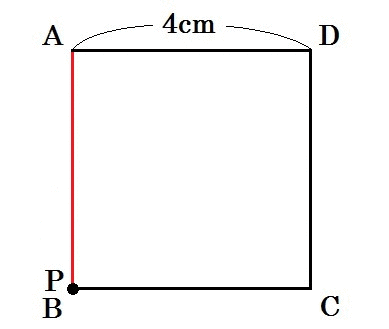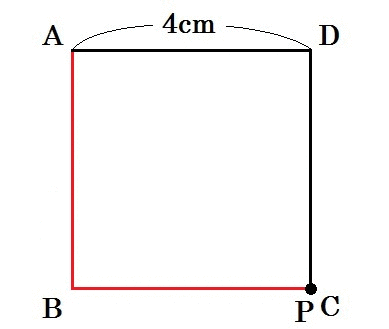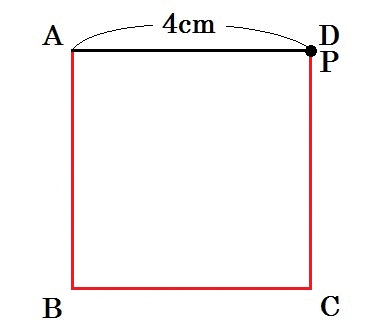
図の赤い線が、点Pの通った跡です。
赤い線は時間の経過とともに何cmになるかというと、毎秒1cmだから、
1秒で \(1\)cm、2秒で \(2\)cm、3秒で \(3\)cm…
表にまとめるとこうですね。

つまり点Pの通った長さは \(x\) cmと表せる。
これを図に書き加えるんです。
ただ、問題で与えられた図は適切じゃありません。
なぜならこの問題では「点Pが辺CD上にあり、四角形ABCPの面積が10㎠となる」ときの \(x\) を求めよ、だからです。
問題の図は、点Pが辺CD上にないもんね。
そんで四角形ABCPも描かれてないもんね。
なので、点Pが辺CD上にあるような図を自分で新たに描きましょう。
こんなかんじ↓
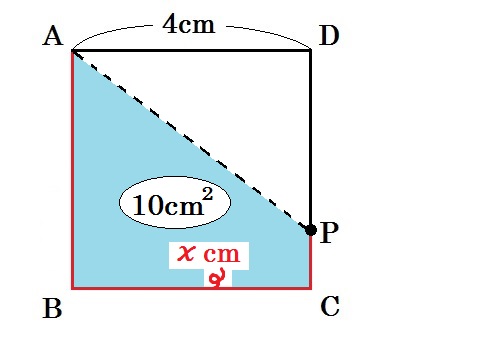
(解説のため色分けしましたが、実際に解く際には斜線などで図形部分を区別するといいでしょう)
さあ、あとは何すればいいんだっけ?
そう、残りの長さをぜんぶ、\(x\) も使って書きこむんでしたね。
ABは \(4\) cm、BCも \(4\) cm 。
CPとPDの長さはやっかいですが、よーく考えたらわかります。
難しければ、辺をまっすぐにした以下の図を参考にしてください。
この考え方ができると、点の移動問題すべて、ずいぶんラクになりますよ。
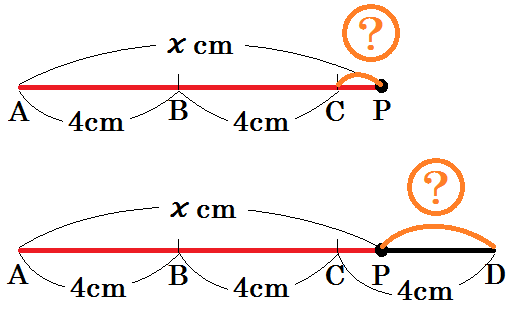
このように考えれば、
CP= \(x-8\) cm
PD= \(12-x\) cm と表せます。
これでやっと、方程式をつくる準備が完了しました。
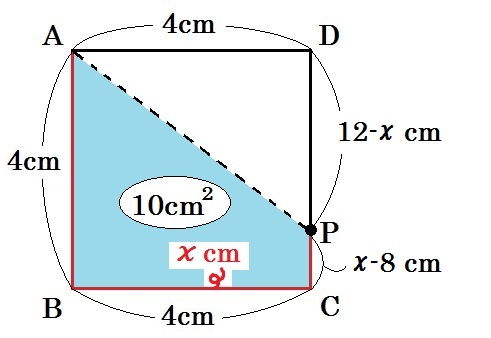
四角形ABCPは台形です。んで面積が10㎠です。
$$ \mbox{(上底+下底)} \times \mbox{(高さ)} \times \frac{1}{2} = \mbox{(台形の面積)}$$
でしたね。
よって、方程式と、その後の解法例は以下のとおり。
\begin{eqnarray} \lbrace (x-8)+4 \rbrace \times 4 \times \frac{1}{2} &=& 10 \\ (x-8+4) \times 4 &=& 20 \\ x-4 &=& 5 \\ x &=& 5+4 \\ x &=& 9 \end{eqnarray}
答.9秒後
以上のように、点の移動する問題、つまり動点の問題では
まず点の通った長さを \(x\) で表す
残りの長さを表すのが難しいときは辺をまっすぐにして考える
この2つが解き方のコツになります。
練習問題
なお、例題4には別の解き方もあります。
三角形APDの面積で方程式をつくる方法です。
つまり△APD=正方形ABCD-四角形ABCP
という関係から解くやりかた。↓
解)四角形ABCPの面積が10㎠となるのは、点PがAを出発してから \(x\) 秒後とする。

\begin{eqnarray} (12-x) \times 4 \times \frac{1}{2} &=& 16-10 \\ (12-x) \times 2 &=& 6 \\ 12-x &=& 3 \\ -x &=& 3-12 \\ -x &=& -9 \\ x &=& 9 \end{eqnarray}
答.9秒後
どちらの方法でもかまいません。
自分の解きやすいほうで解きましょう。
ただ、どっちの方法で解くにしても、注意すべき点。
それは方程式をつくる前の「図に書きこむ」という作業を怠らないことです。
この作業を怠っておいて、「わからない」「できない」となっている中学生がいかに多いか。
特に動点の問題では、方程式をつくるまえに
- まず点の通った長さを \(x\) で表す
- 残りの長さをすべて書きこむ
という2つのすべきことがあると肝に銘じてください。
以下の練習問題でも、それは同様です。
数学に王道なし。
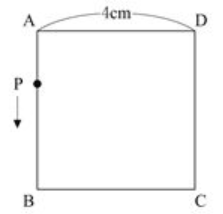
問4)下図のような台形ABCDで、点Pは辺AB上を、AからBまで毎秒3cmの速さで動く。三角形APDと三角形BPCの面積が等しくなるのは、点PがAを出発してから何秒後か。
答.3秒後
まとめ
方程式文章題における「図形問題」の解き方のコツ。
≪まず基本は…≫
- 図がなかったら自分できれいに描くこと
- \(x\) も使って長さをぜんぶ書きこむこと
*面積の公式を忘れていたらその復習も。
≪長方形で周の長さが与えられたら…≫
(たて)+(よこ)=周の長さの半分
この関係式をつかって方程式をつくること。
*「BはAより~」「BはAの~倍」だったらAのほうを \(x\) とする。
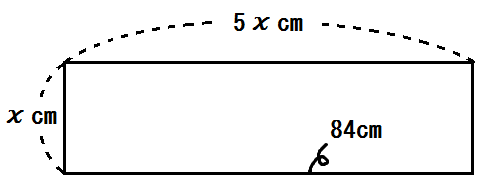
≪円をふくむ図形問題では…≫
円の半径はどこでも同じ長さ
この事実を思い出すこと。
*そして表せる長さをどんどん表していく。とくに難問ほどこれが有効。
≪点が移動する(動点の)問題では…≫
まず点の通った長さを \(x\) で表す
残りの長さを表すのが難しいときは辺をまっすぐにして考える
*たとえ方程式をつくる見通しが立たなくても、長さを図に書きこんでいくという姿勢を怠らない。

以上、図形問題における解き方のコツでした。
模試や受験、またSPI問題などすべての図形問題に応用できるコツですので、ぜひおぼえて使ってください。
[関連記事]
これで中学数学における 1次方程式 文章題の解説を終わります。
なお、方程式 文章題における「規則性の問題」の解き方については、以前「文字と式」で解説したコツを使うだけなので省略します。
規則性問題ができないという場合はこちらの記事を復習してください↓

次回からは「比例・反比例」の単元に入ります。
そもそも関数とは何か?
座標とは?グラフとは?
比例か反比例かを見分けるコツは?
中学生のつまずきやすいポイントにしぼって、コツを解説していきます。
[1次方程式文章題のその他の記事はこちらから↓]









コメント
最初の三角形の元の高さを求める問題の解説が欲しいです。
もとの三角形の高さをxcmとする。
12×(2x+5)× 1/2 = 12× x × 1/2 +54
6(2x+5)=6x+54
2x+5=x+9
x=4
サイトの冒頭に載せてある高校入試の問題の問い2の途中式お願いします。
長さを図に書き込む、というのは、確かに大切なポイントですが、
「全部」書き込む、というのは、私とはアプローチが違うな、と思いました。
確かに、手も足も出ないときは、とりあえず「全部」書き込む、
という手段も有効でしょう。
しかし、それだと時間がかかります。
やはり、効率良く問題を解くためには、
必要な部分のみ長さを書き込む(どこが必要な部分かを考える)
ことも大切だと思います。
(上の例題レベルの問題なら、全部書き込んでも、たいして時間はかかりませんが)
もっとも、それは、習熟したら(問題のレベルが上がったら)やればいいことで、
導入期には、「とりあえず全部書け」がいいのかもしれませんね。