中学数学「１次方程式」文章題の解き方⑤【過不足の問題】

中１数学「１次方程式」文章題。

５回目は過不足の問題の解き方について。

過不足問題を解くコツを教えてほしい・・・

「余る」と「足りない」をどう見分けて式を作ったらいいかわからない・・・

長椅子の問題の解き方を知りたい・・・

こんな中学生に活用ください。

 

過不足の問題は中学の定期テストでも頻出しますが、苦手とする生徒も多い問題です。

なぜ過不足問題が出るとできない・わからないとなるのか？

その原因をつきつめると２点に集約されます。

1. 未知数が２つあるため、どちらを \(x\) と置いたらいいかわからない
2. 「余る」「足りない」等の文章から機械的に立式したらまちがえる

この２つの原因を解決して、かんたんに解くコツをいまから伝授します。

さきに結論から言うと、まず１．を解決するコツは、少ない方を \(x\) とすること。

そして２．を解決するコツは、イラストを描いたり具体的な数字を入れてイメージすることです。

実際どうやって解いていくのか、例題とともにやっていきましょう。

*連立方程式の過不足問題はこちら

過不足の問題　基本

まずは過不足問題の基本から。

この例題のように、あめや鉛筆やリンゴを配って余ったり不足したりといった問題です。

例題１を読むと、求めるものが「子どもの人数」「あめの個数」と２つあります。

このように過不足の問題では未知数が２つ出てきますが、どんな問題でも通用する解き方のコツ。

それが以下の手順です。

①少ない方を \(x\) とする

②多い方の数量を、\(x\) を使って２通りの式で表す

③２つの式を＝で結べば方程式ができる

実際にやってみましょう。


スポンサーリンク

解き方のコツ

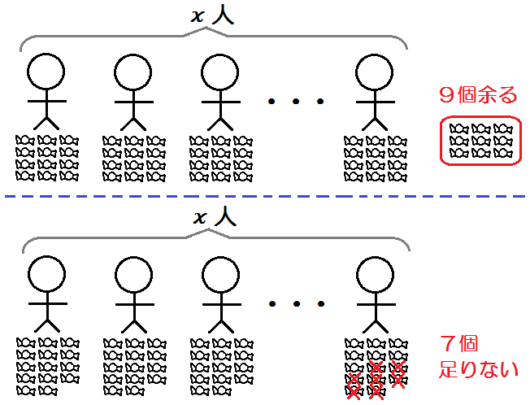
例題１）子どもに１人12個ずつあめを配ると9個余り、14個ずつ配ると7個足りない。子どもの人数とあめの個数を求めよ。

まず、子どもの人数とあめの個数、どちらが少ないか考えます。

子どもにあめを配るんだから、当然、子どもの人数のほうですね。

よって一行目は「子どもの人数を \(x\) 人とする。」

 

次に、多い方の数量、つまりあめの個数を２通りで表していきます。

「１人12個ずつあめを配ると9個余り」。

この文から、あめの個数を表す式をつくると？

そう、\(12x+9\) ですね。

「14個ずつ配ると7個足りない」。

この文から、あめの個数を表す式をつくると？

そう、\(14x-7\) ですね。

こうして \(x\) を使って２通りの式がつくれるわけです。

（この段階で難しいという場合はイラストを描いたり具体的な数字を入れてイメージします。くわしくはすぐ次の章で解説しています）。

 

この２つの式を＝で結べば、それだけで方程式のできあがりです。

$$ 12x+9=14x-7 $$

あとは解いて、確かめて、単位をつけて答えを書く。

ただ「あめの個数」も求めよ、なので、左辺か右辺どっちかに \(x=8\) を代入して計算することを忘れないようにしなくちゃいけません。

最初から最後まで解くと、以下のとおりです。

 

以上のように、過不足の問題はすべて

①少ない方を \(x\) とする

②多い方の数量を、\(x\) を使って２通りの式で表す

③２つの式を＝で結べば方程式ができる

という３つの手順をふめば、かんたんに方程式をつくることができます。

このコツはあらゆる過不足問題に当てはまり、例外はありません。

ぜひおぼえて使ってください。

 

 

練習問題

ここで注意点を２つほど。

過不足の問題を解説した記事や動画には、「人数の方を \(x\) としなさい」という指導もあります。

ジュウゴも一時期そう教えていました。

しかし問２や例題３の「長椅子の問題」などのように、人数を \(x\) と置くとややこしくなる問題もあるんです。

だから「人数の方を \(x\) としなさい」というのは、まちがいじゃないけど、限定的にしか使えない方法です。

そうではなくて、「少ない方を \(x\) とする」とおぼえていたら、これには例外がありません。

ぜひこっちで解いてください。

 

それから、実は多い方を \(x\) とおいても方程式を作ることはできます。

例題１で「あめの個数を \(x\) 個とする」としたら、方程式は以下になります。

$$ \frac{x-9}{12} = \frac{x+7}{14} $$

ただ、見てわかるとおり作りづらいし、たいてい分数が出てくるので解くのもめんどい。

だからやっぱり、少ない方を \(x\) とおいたほうがラクなんです。

 

さて余談はこれくらいにして、練習問題を２つ載せます。

解答は末尾に記載、質問はコメント欄からどうぞ。

問１）生徒に鉛筆を配るのに、１人6本ずつ配ると22本足りないので、１人5本ずつ配ると10本余った。生徒の人数と鉛筆の本数を求めよ。
答．生徒３２人、鉛筆１７０本

問２）1冊130円のノートを何冊か買おうとしたが、所持金では160円不足する。そこで1冊108円のノートを同じ冊数だけ買おうとしたところ、まだ6円だけ不足した。買おうとしたノートの冊数と所持金を求めよ。

問１）生徒３２人、鉛筆１７０本
問２）ノート７冊、所持金７５０円

＞Amazonプライム・ビデオ「DEATH NOTE　デスノート」

 

過不足の問題　応用１

次に、過不足問題の応用として、「何人かで一定の金額を集める問題」をやっつけます。

例題２のようなやつですね。

この例題、「900円余る」「800円足りない」という文をあまりよく考えずに「余るから＋」「足りないから－」と捉えて

$$ 350x +900 = 300x -800 $$

とやったら、まちがいなんです。

なぜまちがいなのか？

正しい方程式をつくるにはどうしたらいいのか？

それをわかるためのコツが、

• イラストを描く
• 具体的な数字を入れて考える

になります。

 

解き方のコツ

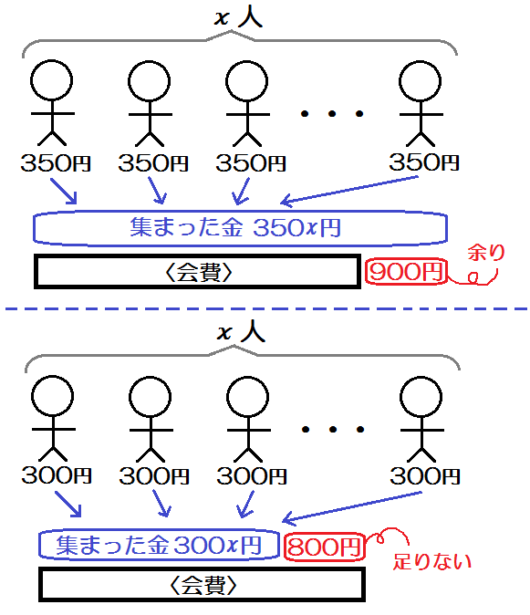
例題２）クラス会の費用を集めるのに、１人350円ずつ集めると900円余り、１人300円ずつ集めると800円足りない。クラス会の人数と費用を求めよ。

まずクラス会の人数と費用、どっちが少ないか考えて、「クラス会の人数を \(x\) 人」とします。

人数が300人以上とかまずありえないもんね。ここまでは基本です。

 

次に多い方の数量、つまりクラス会の費用を、\(x\) を使って２通り表していきます。

ここで、「余るから \(+900\) だ」「足りないんだから \(-800\) だ」と安易に考えてはいけません。

「何人かで一定の金額を集める問題」では、余るで－、足りないで＋と逆になるんです。

なぜか？

たとえばこんなイラストを描けばわかります↓

上のイラストでは、会費＝350 \(x\) -900

下のイラストでは、会費＝300 \(x\) +800

こうなるわけが一目瞭然ですね。

このように、「何人かで一定の金額を集める問題」等で立式が難しい場合は、自分でかんたんなイラストを描いてイメージするといいでしょう。

とくに上図のように横棒グラフっぽく描くと、数量どうしの関係が一目でわかるので、おススメです。

 

それでもわからない、式が表せない。

そんな場合は、\(x\) に具体的な数字をてきとうに入れて考えるといいでしょう。

たとえば \(x=10\) 、つまりクラス会の人数が10人だとします。

350円ずつ集めると、集まったお金は、3500円ですね。

この3500円からクラス会の費用を出しても900円余るんです。

クラス会の費用はいくら？

そう、2600円。

いま何算しましたか？

そう、\(3500-900\) と－しましたね。

だから10をもとの \(x\) に戻すと、式は \(350x-900\) となるわけです。

同様にして、「300円ずつ集めると800円足りない」も具体的な数字を入れると立式しやすくなります。

このあたりのコツは「１次方程式文章題①」でも解説したものです。

復習したいという方は以下のリンクからどうぞ。

中学数学「１次方程式」文章題の解き方①【代金、個数】

中学数学のつまずき解消をめざすこの連載。 今回からいよいよ「１次方程式の利用」、つまり文章題に入ります。 方程式の文章問題を解く手順は以下のとおりです。 (1)求めるものを \(x\) とする (2)等し...

jugo-blog.com

2018.08.21

 

以上のように、過不足問題において方程式を立てるのが難しい場合は、

• かんたんなイラストを描く
• \(x\) に具体的な数字を入れて何算するか考える

この２つのコツを利用して、立式してみてください。

ちなみに例題２を全部解くと、以下のとおりです。

 

練習問題

ここでも注意点をひとつ。

「何人かで一定の金額を集める問題」だったら、「余る」と「足りない」で＋－が逆なんだ・・・。

こんなふうにパターン化しておぼえていても、まあ解けます。

ただ、一定水準以上の学力がある生徒には、最初からこうしてパターン化する解き方はおススメしません。

なぜなら、初めの深い理解・納得がぬけちゃうからです。

「正負の数②　累乗」の記事でも書きましたが、数学のパターン化は初めに納得してから行わないと、記憶が強固になりません。

イラストを描いたり具体的な数字を代入して考えて、なぜそうなるのか、まず納得する。

パターン化で解くのは、それからにしてください。

 

では、練習問題をどうぞ。

問３）あるグループでツアー旅行をすることになった。ツアーの旅行代金として、１人9000円ずつ集めると2200円余るが、１人8500円ずつ集めると1800円足りない。グループの人数と旅行代金を求めよ。

問４）マネージャーのお見舞いに部員全員で花を買うことにした。花代として１人300円ずつ出すと200円足りないが、１人350円ずつ出すと350円余る。部員の人数と花代を求めよ。

問３）グループ８人、旅行代金６９８００円
問４）部員１１人、花代３５００円

*連立方程式の過不足問題はこちら

 

過不足の問題　応用２

最後に「長椅子の問題」です。

この例題３のように長椅子が出てくる文章題も、過不足の応用問題のひとつとして頻出しますが、しかしここまで読み進めたあなたなら決して難しくありません。

いままでのコツを使ってスッと解いていくことができるでしょう。

 

解き方のコツ

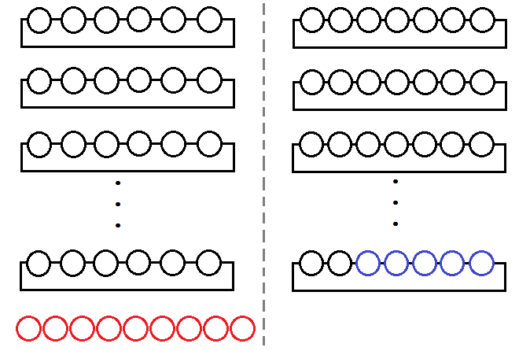
例題３）体育館に長いすを並べて生徒が座っていく。１脚の長いすに6人ずつ座ると9人の生徒が座れず、7人ずつ座ると5人分の席が余る。生徒の人数と長いすの数を求めよ。

まず求めるものは「生徒の人数」と「長いすの数」です。

どっちが少ないですか？

そう、「長いすの数」ですね。１脚に何人かずつ生徒が座るもんね。

よって一行目は「長いすの数を \(x\) 脚とする。」

 

次に多い方の数量、つまり生徒の人数を２通りで表していきます。

難しい場合は、イラストを描いたり、\(x\) に具体的な数字を入れたりして考えます。

たとえばイラストならこんなのとか。

左のイラストから、生徒の人数は \(6x+9\)

右のイラストから、生徒の人数は \(7x-5\)

よって以下、

 

このように、過不足の文章題は長椅子の問題であっても、以下の手順で。

1. 少ない方を \(x\) とする
2. 多い方の数量を、\(x\) を使って２通りの式で表す
3. ２つの式を＝で結べば方程式ができる

そして立式が難しい場合は以下２つのコツを使って。

• かんたんなイラストを描く
• \(x\) に具体的な数字を入れて何算するか考える

全部やっつけていってください。

 

練習問題

それでは最後の練習問題です。

質問はコメント欄からどうぞ。

問５）地域の子どもたちで宿泊施設に合宿をした。１部屋に4人ずつ泊まると5人が入れなくなり、１部屋に5人ずつ泊まると最後の１室だけ3人部屋になる。参加した子どもの人数と、宿泊施設の部屋数を求めよ。

問６）顕微鏡が何台かある。１台を2人で使えば6人の生徒が使えなくなる。そこで１台を3人で使ったら最後の１台は1人で使うことになり、顕微鏡が２台余った。生徒の人数と顕微鏡の台数を求めよ。

問５）子ども３３人、７部屋
問６）生徒３４人、顕微鏡１４台

＞Amazonプライム・ビデオ「はたらく細胞」

 

まとめ

中１数学「１次方程式」文章題で、過不足の問題が出てきたら・・・

解き方のコツは以下の手順をふむこと。

①少ない方を \(x\) とする

②多い方の数量を、\(x\) を使って２通りの式で表す

③２つの式を＝で結べば方程式ができる

＊「人数を\(x\)とする」方法が使える問題は限定的。「少ない方を\(x\)とする」方法に例外はない。

＊多い方の数量を\(x\)とおいても式は立つが、ややこしいのでおススメしない。

 

また方程式を立てるのに難しい場合は、以下２つのコツを使ってイメージすること。

○かんたんなイラストを描く

○\(x\) に具体的な数字を入れて何算するか考える

＊「何人かで一定の金額を集める問題」だけ「余る」と「足りない」で＋－が逆、とパターン化して解いてもいいが、まず初めに理解・納得してから。

 

 

次回は「速さ・時間・道のり」の問題について解説します。

方程式文章題のなかでも、いや中学数学のなかでも特にややこしい個所ですが、安心してください。

はいてますよ。

コツがありますよ。

→中学数学「１次方程式」文章題⑥【速さ・時間・道のり】