中学数学「１次方程式」文章題の解き方②【分配、年齢、貯金】

前回につづいて、中学数学「１次方程式」文章題の解き方のコツを解説していきます。

今回は「分配問題」「年齢問題」「貯金問題」の解き方について。

文章題がわからない、できないという中学生はぜひ参考にしてください。

 

方程式における「分配」「年齢」「貯金」の文章問題は、その解き方のコツがすべて同じです。

前回の記事でもすこし書きましたが、方程式を立てるとき、２段階にわけて考えればいいんです。

①分配したり、年月が経ったり、貯めたり下ろしたりした後の数を x を使って表す

②文に沿って等式（＝方程式）をつくる

以下、具体的な解き方を見ていきましょう。


スポンサーリンク

分配問題の解き方

このような分配の問題、１次方程式の文章題ではたまにみかけますね。

兄から弟へ、または姉から妹へ、絵はがきやクッキーやおはじきを渡すという問題です。

方程式文章題の手順にそって、丁寧にやっていきます。

 

分配問題のコツは…

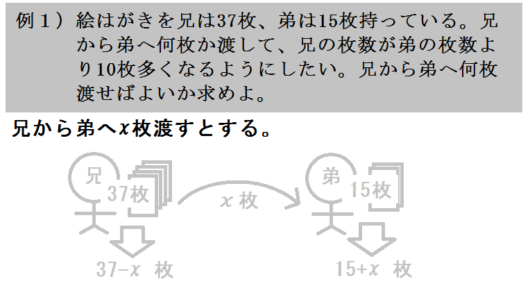
例題１）兄は絵はがきを37枚、弟は15枚持っている。兄から弟へ何枚か渡して、兄の枚数が弟の枚数より10枚多くなるようにしたい。兄から弟へ何枚渡せばよいか求めよ。

まず求めるものは「兄から弟へ何枚渡せばよいか」です。

よって一行目には、「兄から弟へ \(x\) 枚渡すとする」等と書きます。

 

次に方程式をつくります。

このとき、２段階にわけて考えるというのが解き方のコツになります。つまり、

①分配した後のそれぞれの数を表す

②文に沿って等式をつくる

です。

 

①分配した後のそれぞれの数を表す

兄は37枚持っていて、弟に \(x\) 枚渡しました。

兄はいま、何枚の絵はがきを持っていますか？

そう、\(37-x\) 枚ですね。

また弟は15枚持っていて、兄から \(x\) 枚もらいました。

弟はいま、何枚の絵はがきを持っていますか？

そう、\(15+x\) 枚ですね。

 

このように、まず分配後のそれぞれの枚数を \(x\) を使って表します。

それから初めて、方程式（等式）を作っていくんです。

 

②文に沿って等式をつくる

前回解説した「残金の問題」と同じように、「分配の問題」にも、文章中に等しい関係を表す文が必ずあります。

この例題の場合は「兄の枚数が弟の枚数より10枚多くなる」が、それです。

この文に沿って、あれこれ難しく考えず、等式をつくればいいんです。

つまりこれ。

$$ 37-x=(15+x)+10 $$

 

こうして方程式がつくれたら、あとは方程式を解き、確かめをして、答えを書くだけです。

\begin{eqnarray} 37-x &=& 15+x+10 \\ -x-x &=& 15+10-37 \\ -2x &=& -12 \\ x &=& 6 \end{eqnarray}

答．６枚

 

以上のように、分配の問題では、

①分配後のそれぞれの数を \(x\) を使って表す

②等しい関係を表す文どおりに、等式をつくる

という２段階にわけて方程式を立てるといいでしょう。

 

練習問題

分配の練習問題を２つほど載せておきます。

上の解き方にそって、解いてみてください。

なお解答は末尾に記載、質問はコメント欄からどうぞ。

また方程式文章題の基本の解き方を忘れたという人は、前回の記事を参考にしてください。

(連立方程式の分配問題はこちらへ)

問１）クッキーを姉は15個、妹は6個つくった。姉から妹へ何個か渡すと、姉の個数が妹の個数の半分になった。姉から妹へ何個渡したか？

問２）花子とアンはおはじきを20個ずつ持っている。アンから花子へ何個か渡すと、花子の個数はアンの３倍より４個多くなった。アンから花子へ何個渡したか？

問１）８個
問２）１１個

 

年齢問題の解き方

次に年齢の問題について解説します。

１次方程式の文章題では、これらの例題のような年齢問題もよく出てきます。

わからない・できないという中学生も多いですが、安心してください。

解き方のコツは分配問題といっしょです。

 

年齢問題のコツは…

例題２）現在、父は48歳で子は14歳である。父の年齢が子の年齢の３倍になるのはいまから何年後か？

まずは例題２から解いていきましょう。

例題２の求めるものは「いまから何年後か」なので、一行目には「いまから \(x\) 年後とする」等と書きます。

 

次に方程式をつくります。

このときのコツも２段階。つまり、

①x 年後（または x 年前）のそれぞれの年齢を表す

②文に沿って等式をつくる

です。

 

① \(x\) 年後のそれぞれの年齢を表す

父はいま48歳です。

\(x\) 年後には何歳になりますか？

そう、\(48+x\) 歳ですね。

また子はいま14歳です。

\(x\) 年後には何歳になりますか？

そう、\(14+x\) 歳ですね。

 

このように、まず \(x\) 年後（または \(x\) 年前）のそれぞれの年齢を \(x\) を使って表します。

（わからないという中学生は、\(x\) の代わりに具体的な数字を入れて考えてみるといいでしょう。たとえばいまから５年後、父は何歳になりますか？そう、53歳ですね。「53」は何算で出しましたか？そう、\(48+5\) というたし算ですね。だからいまから \(x\) 年後の父の年齢は \(48+x\) 歳なんです）。

それから方程式（等式）を作っていきます。

 

②文に沿って等式をつくる

「年齢の問題」にもやはり、等しい関係を表す文が必ずあります。

例題２の場合は「父の年齢が子の年齢の３倍になる」が、それに当たります。

この文に沿って、あれこれ難しく考えず、等式をつくるだけ。

$$48+x=3(14+x)$$

 

あとは方程式を解き、確かめをして、答えを書くだけです。

\begin{eqnarray} 48+x&=&3(14+x) \\ 48+x&=&42+3x \\ x-3x&=&42-48 \\ -2x&=&-6 \\ x&=&3 \end{eqnarray}

答．３年後

 

以上のように、年齢の問題でも、

① \(x\) 年後（または \(x\) 年前）のそれぞれの年齢を \(x\) を使って表す

②等しい関係を表す文どおりに、等式をつくる

という２段階にわけて方程式を立てましょう。

 

練習問題

ちなみに例題３を解くと、以下のとおりです。

例題３）現在、母の年齢は46歳で、３人の子の年齢は16歳、18歳、20歳である。母の年齢が３人の子の年齢の和と等しかったのはいまから何年前か？

解）いまから \(x\) 年前とする。

\begin{eqnarray} 46-x&=&(16-x)+(18-x)+(20-x) \\ 46-x&=&16-x+18-x+20-x \\ -x+x+x+x&=&16+18+20-46 \\ 2x&=&8 \\ x&=&4 \end{eqnarray}

答．４年前

上で紹介した解き方のコツを使えば、方程式を立てるのもむずかしくないでしょう。

それでは年齢の練習問題も２つほど載せておきます。

（答は末尾に記載）

問３）現在、祖父は71歳でふたりの孫は15歳と13歳である。祖父の年齢が孫の年齢の和の２倍と等しくなるのはいまから何年後か？

問４）母が24歳のときに生まれた子どもがいる。母の年齢が子の年齢の３倍になるのは、母と子それぞれ何才のときか？

問３）５年後
問４）母３６歳、子１２歳

 

 

貯金問題の解き方

最後に貯金の問題について解説します。

例題４のような、毎月貯めていったり毎月下ろしていったりする問題です。

この貯金問題も、分配問題や年齢問題と解き方はまったく同じです。

 

貯金問題のコツは…

例題４）Ａは4000円、Ｂは2600円の貯金がある。来月からＡは毎月300円、Ｂは毎月500円ずつ貯金していく。２人の貯金が等しくなるのはいまから何か月後か？

まず求めるものは「いまから何か月後か」なので、一行目には「いまから \(x\) か月後とする」等と書きます。

 

次に方程式をつくります。

もうコツはわかりますね！？

①x か月後（または x か月前）のそれぞれの貯金を表す

②文に沿って等式をつくる

この２段階の解き方でいけば方程式を立てることができます。

 

① \(x\) か月後のそれぞれの貯金を表す

Ａは毎月300円の貯金を \(x\)か月しました。

貯まった金額は、\(300x\) 円になります。

それにもともと4000円持っていたのだから、Ａの貯金はぜんぶで？

そう、\(300x+4000\) 円ですね。

またＢは毎月500円の貯金を \(x\)か月しました。

貯まった金額は、\(500x\) 円になります。

それにもともと2600円持っていたのだから、Ｂの貯金はぜんぶで？

そう、\(500x+2600\) 円ですね。

 

このように、まず \(x\) か月後（または \(x\) か月前）のそれぞれの貯金を \(x\) を使って表します。

（わからないという中学生は、やはり \(x\) の代わりに具体的な数字を入れて考えるといいでしょう。たとえばＡは毎月300円の貯金を５か月したとします。貯まった金額は1500円、これは \(300 \times 5\) というかけ算です。この1500円と、もともと持っていた4000円のたし算をして、Ａの貯金額5500円が出ますね。よって \(x\) ヶ月貯金したならば、Ａの貯金額は \(300x+4000\) なんです）。

それから等式をつくります。

 

②文に沿って等式をつくる

「貯金の問題」にもやっぱり、文章中に等しい関係を表す文が必ずあります。

例題４の場合、「２人の貯金が等しくなる」がそれ。

もうむずかしくないですね。

等式をつくりましょう。

$$300x+4000=500x+2600$$

 

あとは方程式を解き、確かめをして、答えを書くだけです。

\begin{eqnarray} 300x+4000&=&500x+2600 \\ 300x-500x&=&2600-4000 \\ -200x&=&-1400 \\ x&=&7 \end{eqnarray}

答．７か月後

 

以上のように、貯金の問題でも、

① \(x\) か月後（または \(x\) か月前）のそれぞれの貯金を \(x\) を使って表す

②等しい関係を表す文どおりに、等式をつくる

という解き方でいくとカンタンに方程式をつくることができます。

 

練習問題

貯金の練習問題も２つ載せておきます。

（答は末尾に記載）

上の解き方でがんばってみてください。

くりかえしになりますが、方程式文章題の基本の解き方が身についていないという中学生は前回の記事から復習してください。

また、それでもなおできない・わからない場合があれば、コメント欄から気軽に質問ください。回答します。

問５）兄と弟はともに１万円持っている。来月から兄は毎月1000円、弟は毎月2500円ずつ貯金していく。弟の貯金額が兄の貯金額のちょうど２倍になるのはいまから何か月後か？

問６）姉は9500円、妹は5500円の貯金がある。ふたりとも来月から毎月500円ずつ貯金をおろして使うことにした。姉の貯金が妹の貯金の３倍になるのはいまから何か月後か？

問５）２０か月後
問６）７か月後

 

 

まとめ

「分配」「年齢」「貯金」問題の解き方のコツは、方程式を立てるときに次の２段階で考えること。

①分配した後や、x 年後（または x 年前）や、x か月後（または x か月前）のそれぞれの数を x を使って表す

②文章中の、等しい関係を表す文どおりに、等式をつくる

 

次回は１次方程式文章題の「整数、自然数」問題について解説します。

「ある数を４でわったら商が５であまりが２」とか。

「連続する３つの偶数の和が24」とか。

「２けたの自然数の十の位と一の位の数をいれかえて…」とかの解き方です。

次の記事：中学数学「１次方程式」文章題の解き方③【整数、自然数】

(連立方程式の文章題はこちらへ)