中学数学「１次方程式」文章題の解き方⑧【割合の問題】

中１数学 １次方程式の文章題。

８回目は「割合の問題」解き方のコツです。

「定価や利益や割引の計算がわからない」

「食塩水の百分率（ﾊﾟｰｾﾝﾃｰｼﾞ）って苦手」

「去年より○％増えての問題ができない」

こうしたすべてを、この１記事でぜんぶ解決します。割合問題が苦手な中学生の指導にお役立てください。

 

「商品の売買」「食塩水」「増減」…。

これら方程式の割合の問題でつまずく原因は３つです。

• 「1割」「23%」「4割引き」「56%増」などの言葉を計算式に直せない。
• 「原価」「定価」「売り値」「利益」「濃度」といった言葉の意味がよくわかってない。
• それぞれの割合問題の、方程式を立てるときのコツを知らない。

現在指導中の生徒やお子さんが、もし割合が苦手だとしたら、この３つのうちどれかに当てはまります。

ということは、言葉の意味と使い方を知り、それぞれの問題のコツさえつかめば、できるようになります。

実際ジュウゴの指導してきた中学生たちもそうでした。「利益だろうが食塩水だろうが、もうこわくない」になっていきました。

 

そこでこの記事ではまず、割合の定義と計算（使い方）を復習します。

次に「商品」「食塩水」「増減」という問題分野ごとに、出てくる言葉の意味をわかりやすく解説します。

そして同時に、それぞれの問題分野における解き方のコツを紹介していきます。

各段階で、公立高校入試過去問からとった例題を載せるので、問題演習とともに理解していきましょう。

ではどうぞ。

割合の復習

小学５年生で割合を習って以来、割合がどうも苦手…。

「比べる量」と「もとにする量」って、どっちがどっちかわからない…。

先生には「く・も・わ」の公式を使えって言われたけど、何それ…。

こんな中学生はまず、割合とは何かの理解がぬけています。

逆にいえば、割合の理解がきちんとできれば、公式など覚えなくても問題を解くことができます。

割合の定義と使い方を、以下わかりやすく解説します。


スポンサーリンク

割合とは何か？（何割）

割合とは「ある量が基準に対してどれくらいあるかという数値」。

つまり、ざっくりいえば、何倍かってことです。

 

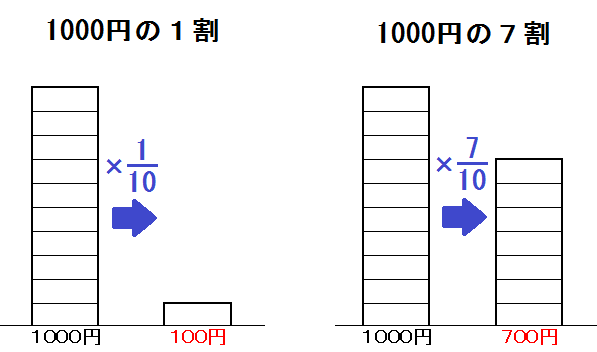
たとえば「１割」とは、基準を10分割したうちの１つ。

つまり、\( \frac{1}{10}\) 倍（0.1倍）ってこと。

なので、1000円の１割は

$$ 1000 \times \frac{1}{10} = 100 \mbox{(円)　だし、} $$

1000円の７割は

$$ 1000 \times \frac{7}{10} = 700 \mbox{(円)　です。} $$

 

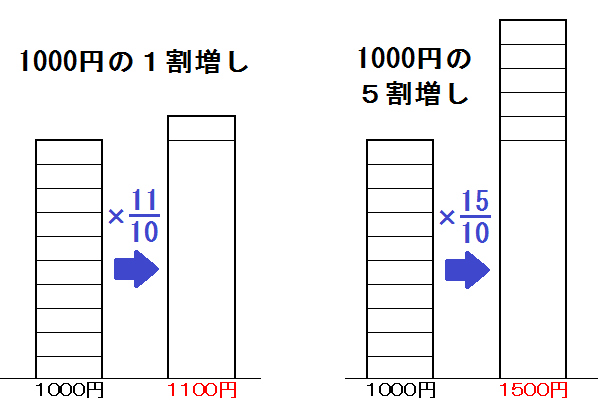
また、\( \frac{11}{10}\) 倍（1.1倍）のことを「１割増」などと言います。

商売の分野では「１割の利益を見込んで」などとよく使います。

なので、1000円の１割増しは

$$ 1000 \times \frac{11}{10} = 1100 \mbox{(円)　だし、} $$

1000円の５割の利益を見込んで値段をつけたら

$$ 1000 \times \frac{15}{10} = 1500 \mbox{(円)　で、} $$

ようするに1.5倍ってことですね。

 

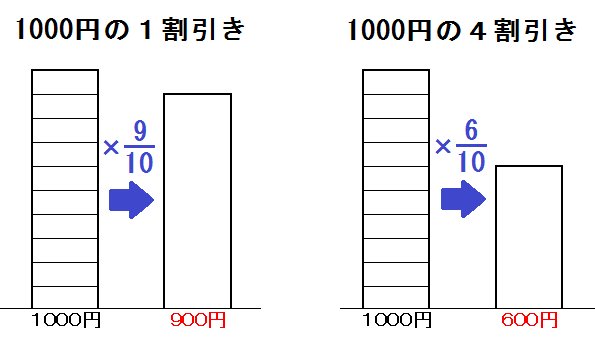
そして、\( \frac{9}{10}\) 倍（0.9倍）のことを「１割減」などと言います。

商売の分野では「１割引き」「１割OFF」などとよく使います。

なので、1000円の１割減は

$$ 1000 \times \frac{9}{10} = 900 \mbox{(円)　だし、} $$

1000円の４割引きは

$$ 1000 \times \frac{6}{10} = 600 \mbox{(円)　です。} $$

つまり「１割減」＝「９割」、「４割引き」＝「６割」ってこと。

 

「４割引きって言わずに、６割で売りますって言えばいいのに」と思いますよね。

でも「８割で売ります！」よりも、「２割引き！」のほうがお得感があって、ついつい買ってしまいそうでしょ？

だから商売では特にこうした表現がよく使われるんです。

 

割合とは何か？（百分率）

百分率（パーセンテージ）も同様です。

 

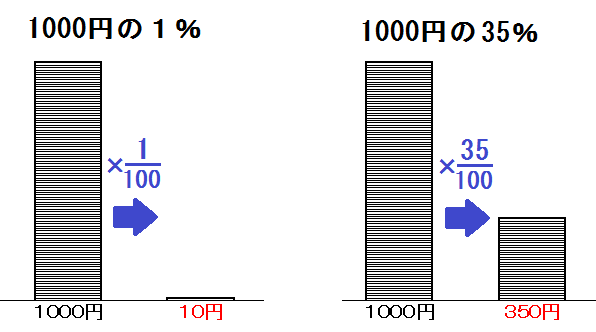
たとえば「１％」とは、基準を100分割したうちの１つ。

つまり、\( \frac{1}{100} \) 倍（0.01倍）ってこと。

なので、1000円の１％は

$$ 1000 \times \frac{1}{100} = 10 \mbox{(円)　だし、} $$

1000円の35％は

$$ 1000 \times \frac{35}{100} = 350 \mbox{(円)　です。} $$

 

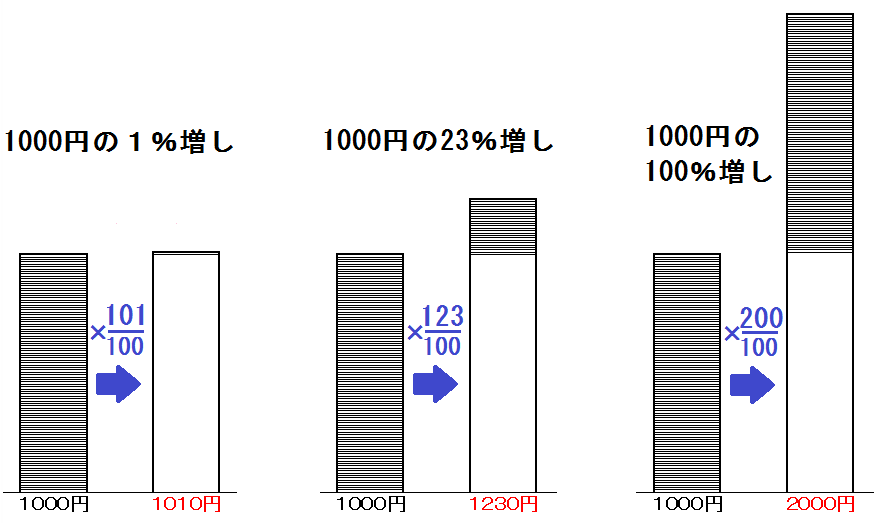
また、\( \frac{101}{100} \) 倍（1.01倍）のことを「１％増」などと言います。

商売の分野では「１％の利益を見込んで」などとよく使います。

なので、1000円の１％増しは

$$ 1000 \times \frac{101}{100} = 1010 \mbox{(円)　だし、} $$

1000円の23％の利益を見込んで値段をつけたら

$$ 1000 \times \frac{123}{100} = 1230 \mbox{(円)　だし、} $$

1000円の100％の利益を見込んで値段をつけたら

$$ 1000 \times \frac{200}{100} = 2000 \mbox{(円)　で、} $$

ようするに２倍ってことですね。

 

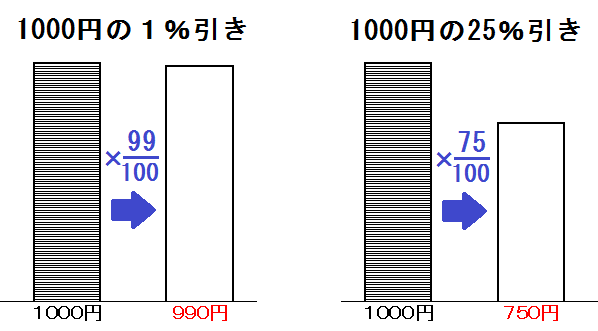
そして、\( \frac{99}{100} \) 倍（0.99倍）のことを「１％減」などと言います。

商売の分野では「１％引き」「１％ＯＦＦ」などとよく使います。

なので、1000円の１％減は

$$ 1000 \times \frac{99}{100} = 990 \mbox{(円)　だし、} $$

1000円の25％引きは

$$ 1000 \times \frac{75}{100} = 750 \mbox{(円)　です。} $$

つまり「１％減」＝「９９％」、「２５％引き」＝「７５％」ってこと。

 

「○％引き」「○％ＯＦＦ」という表現も、商売でよく使うのは、なんとなくお得感があるためです。

「なんと60％のお値段で！」よりも「なんと40％引きのお値段で！」のほうが安く感じるもんね。

どっちも同じことなんだけど。

 

文字式による割合の表し方

以上が割合の定義と、基本的な使い方です。

最後に、文字の入った割合の使い方をおさらいして復習を終わりとします。

以下のまとめをよく読んで、理解してください。

見ただけでは頭に入らないという中学生には、書き写させるといいでしょう。

 

ここまで来れば、冒頭の静岡県高校入試問題も解けるはずです。

例題１）ある中学校では、毎年、多くの生徒が、夏に行われるボランティア活動に参加している。昨年度の参加者は、男子がa人、女子がb人であった。今年度の参加者は、昨年度の男女それぞれの参加者と比べて、男子は9%増え、女子は7%減った。今年度の、男子と女子の参加者の合計を、a,bを用いて表しなさい。（2017　静岡）

表すべき数量は、

（今年度の男子の参加者）＋（今年度の女子の参加者）

ですね。そしてそれぞれを求めるには、

（ \(a\) 人の９％増）＋（ \(b\) 人の７％減）

とすればいい。よって答えは、

$$ \frac{109}{100}a + \frac{93}{100}b $$

この例題が解けたら、割合の復習はひとまず終了としていいでしょう。

 

ここまで割合の定義と計算（使い方）でした。

生徒にさせる際には、「割合ってつまり何倍かってこと」と伝えてあげる、そして図やグラフを用いてビジュアルに訴える。この２点に留意するとわかりやすい説明となります。

それではいよいよ、商品・食塩水・増減問題に入りましょー。

*連立方程式の割合問題はこちら

 

商品の売買の問題

１次方程式の割合における「商品の問題」では、まず言葉の意味を知らなければいけません。

「定価」「原価」「売り値」「利益」などの意味がすっかり腑に落ちてないと、文章を読んでも方程式が立てられないからです。

そこでまず言葉の意味を、中学生にもわかりやすいよう例を用いて説明してから、解き方のコツに入ります。

 

「原価」「定価」「売り値」…とは？

突然ですが、あなたはアパレルショップの店長だとします。

あなたは服を売って、お金を稼いでいます。

さて、まずはじめにするべきことは何か？

売る服を仕入れないといけませんね。

そこでいろいろと服を探したところ、東京の洋服工場がいいシャツを作っていると知りました。あなたはその工場と商談をおこない、送料込みで、一着2000円で買うことができました。

この「2000円」を仕入れ値、または原価と言います。

 

いいシャツが手に入ったので、今度はこのシャツを売りに出します。

さあ、シャツに値段をつけましょう。

何円で売りますか？2000円？

それじゃ儲けがないよね。あなたが利益を得るために、2000円よりも高く売らなきゃ。

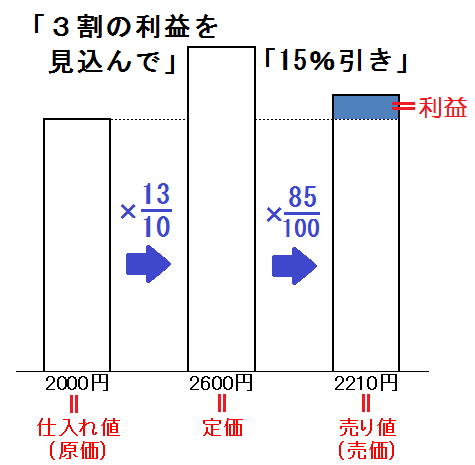
そこで2000円に３割の利益を見込んで値段をつけました。

$$ 2000 \times \frac{13}{10} =2600 \mbox{(円)} $$

この2600円を「定価」と言います。

つまり定価とは、売る側が最初につけた値段のことです。

 

シャツに2600円という値札をつけて、店頭にならべます。

しかし１か月たっても、２か月たっても売れません。

おかしいな、2600円じゃ高いのかな、値下げしようかな。

そう考えたあなたは、定価の15％引きに値下げしました。

$$ 2600 \times \frac{85}{100} = 2210 \mbox{(円)} $$

するとすぐに、ひとりの客がシャツを買っていきました。

「2210円になります、まいどありー！」

この「2210円」が売り値、または売価となります。

つまり売り値とは、実際に商品が売れたときの値段のことです。

お客側からいえば「買い値」または「代金」のことになります。

 

さて、シャツが売れたことであなたには利益が入ります。

一着2000円で仕入れて、2210円で売れました。利益はいくら？

$$ 2210 – 2000 = 210 \mbox{(円)} $$

この「210円」が実際の利益になります。

つまり(売り値)ー(原価)＝(利益)なんです。

 

ただ、ときにはこの利益がマイナスになることもあります。

たとえば定価の15%引きにしても売れなくて、25%引きまで値下げしたとしましょう。

$$2600 \times \frac{75}{100} = 1950 \mbox{(円)} $$

この「1950円」でやっと売れたら、そのときの利益は

$$ 1950 – 2000 = -50 \mbox{(円)} $$

つまり「50円」の損失になるんです。

ずーっと売れないよりは、損失になっても売れたほうがまだお金が入るからいい、という判断も実際の商売ではよくあるからね。

 

以上が「原価」「定価」「売り値」「利益」「損失」の内容です。

イメージできたら、いよいよ問題を解いていきましょう。

 

解き方のコツ

例題２）ある店でシャツを定価の15%引きの価格で買ったところ、定価よりも240円安くなった。このとき、シャツの定価は何円か、求めなさい。ただし、消費税は考えないものとする。（2017 愛知 B）

この例題は、定価や売り値（買い値）という言葉の意味さえ把握していればぜんぜん難しくありません。シャツの定価を \(x\) 円としたら、売り値（買い値）は２通りに表せます。

「定価の15％引きの価格」

$$ x \times \frac{85}{100} $$

「定価よりも240円安くなった」

$$ x -240 $$

よって

このように、「定価」「売り値（買い値）」などの言葉の意味がちゃんとわかること。

これが商品の問題における解き方のコツのひとつといえます。

 

では、次の問題はどうでしょう。

類題１）ある商品に、原価の３割の利益を見込んで定価をつけた。この商品を定価の２割引きで販売したところ、880円の利益があった。この商品の原価は何円か、求めよ。

まずは「原価を \(x\) 円とする」等とします。

次に方程式をつくりますが、原価や利益も出てくる問題では、さっき出てきた利益の関係を使うと等式が立ちます。

(売り値)－(原価)＝(利益)

この３つの数量をそれぞれ表して、最後に関係式に当てはめればいいんです。

原価は \(x\) 円、また利益は \(880\) 円でしたね。

売り値はすこし複雑ですが、順に考えていけば表せますよ。

$$ \frac{13}{10}x \times \frac{8}{10} $$

（原価 \(x\) 円の３割の利益を見込んで定価、その定価の２割引きが売り値だから）。

よって方程式とその後の解答例は↓

以上のように、原価や利益もからむ問題では、

(売り値)－(原価)＝(利益)

この関係式をつかって方程式を立てること。

これが商品の問題におけるもうひとつのコツです。

 

練習問題

では、練習問題を２つ用意しました。

チャレンジさせてみてあげてください。

解答は下に記載、質問はコメント欄からどうぞ。

問１）あるシャツを、以下のように販売する店がある。【通常２枚買う場合：定価の合計金額から500円引き】／【特別期間に３枚買う場合：定価の合計金額から40%引き】。このシャツを特別期間に３枚買う場合は、通常２枚買う場合よりも300円安くなるという。シャツ１枚の定価はいくらか。（2017 鹿児島）

問２）ある商品に、仕入れ値の25%の利益を見込んで定価をつけたが、安売りのとき、定価より360円安く売ったので、仕入れ値の5%の損失になった。この商品の仕入れ値は何円か、求めよ。

問１）４０００円
問２）１２００円

…ちょっと記事が長くなったのでページを分割します。

２ページ目は食塩水の問題と増減の問題について。

＞次ページ「食塩水と増減の問題」

下の「>続きを読む」からでもいけます。