中1数学 1次方程式の速さの文章題。
今回は「まわる・出会う問題」と「速さが変わる問題」を解説します。
「追いつく問題」については前回の記事をごらんください。
前回の内容をかんたんに振り返ると、こんなかんじでした。
速さの文章問題ができない原因は2つ。
- 速さや単位変換に苦手意識がある
- 文章の全体像がつかめない
1.の場合は、まず小学校の復習を5段階でおこなうこと。
2.の場合は、「道のり」「速さ」「時間」を3行に分けた表のような線分図を描き、3項目すべてを埋めること。
そして単位のそろってない文章題では、速さに単位を合わせること。
この3つが速さ問題の解き方のコツだと。
線分図の描き方
詳しくは前回の記事
→中学数学「1次方程式」文章題⑥【速さ・時間・道のり】
今回は、以上のコツが「まわる・出会う問題」「速さが変わる問題」にも適用できることを見ていきます。
前回同様、例題はどちらも公立高校入試の過去問から。
ではいきましょー。
まわる・出会う問題
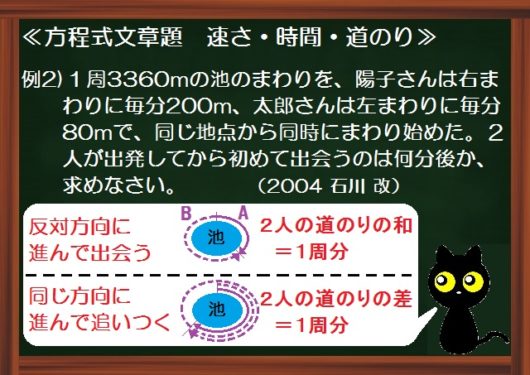
この例題2のように、池や湖やトラックのまわりを、反対方向に進んで出会ったり、同じ方向に進んで1周遅れにして追いついたり。こんな問題がいわゆる「まわる・出会う問題」です。
前回の「追いつく問題」では、道のりが等しいことから方程式が立ちました。
この「まわる・出会う問題」も道のりで方程式が作れます。つまり、
反対方向に進んで出会う:2人の道のりの和=1周分
同じ方向に進んで追いつく:2人の道のりの差=1周分
となるのです。
そしてこのこともやはり、線分図をきれいに描ければ一目でわかります。
解き方のコツ
例題2)1周3360mの池のまわりを、陽子さんは右まわりに毎分200m、太郎さんは左まわりに毎分80mで、同じ地点から同時にまわり始めた。2人が出発してから初めて出会うのは何分後か、求めなさい。(2004 石川 改)
まず何はともあれ、求めるものを \(x\) とします。よって一行目は
「2人が出発してから初めて出会うのは \(x\) 分後とする」。
またこの問題は単位変換も必要ないですね。
道のりも時間も、速さに単位がそろってるもんね。
よって次に線分図を描きます。
「まわる・出会う問題」はどんな線分図を描くよう習いましたか?
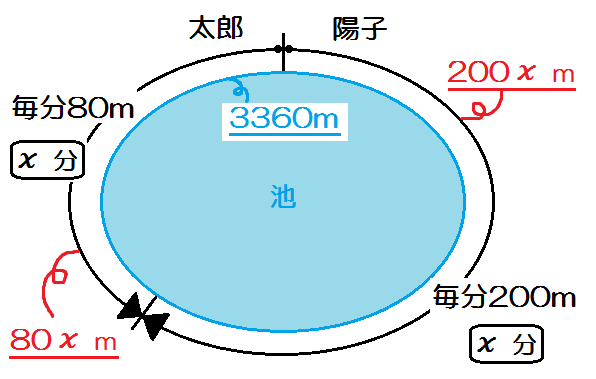
こんなの?↑
これでもいいんです。問題に忠実に描いた線分図です。
ただこの線分図では、「道のり」「速さ」「時間」の3項目をすべて埋めたか、わかりにくいんですね。
また「出会う」ほうはまだいいんですが、「1周遅れで追いつく」ほうの問題になると、何周も矢印を描かなくちゃいけなくて非常にごちゃごちゃします。
それでわたしは最近、こっちをおススメしています↓
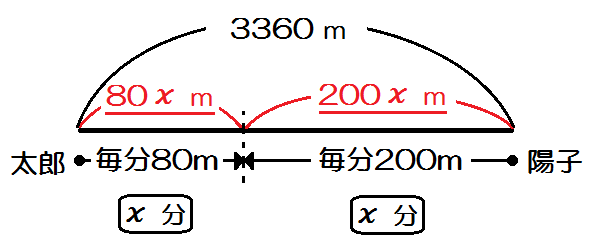
つまり、出発点を両端に分けてまっすぐにした線分図です。
これだと「道のり」「速さ」「時間」の3項目を上から3段に分けてきれいに描くことができます。よってすべての項目を数字や文字式で埋めたか埋めてないか、一目でわかります。
文章に沿って線分図を描いていけば、まだ埋まっていないのは「2人の道のり」だとわかる。だから、それぞれ速さ×時間=道のりで、太郎と陽子の道のりを表すことができます。
そしてこっちの線分図のほうが、等しい関係もわかりやすいでしょう。
(太郎の道のり)+(陽子の道のり)=3360m だと。
$$ 80x + 200x = 3360 $$
あとは方程式を解いて、確かめて、答えを書くだけです。
\begin{eqnarray} 80x + 200x &=& 3360 \\ 280x &=& 3360 \\ x &=& 12 \end{eqnarray}
答.12分後
以上のように、「まわる問題」で反対方向に進んで出会う場合は、出発点を両端に分けたまっすぐな線分図を描くとよりわかりやすい。
そこから「2人の道のりの和=1周分」という方程式が立つ。
ぜひ参考にしてください。
ちなみにこのコツは「まわる問題」だけでなく、向かい合って進んで出会う問題にも使えます。下に載せた練習問題の問4などがそうです。
単位変換を含んだ類題
類題2)周囲が4kmの湖のまわりをまわるのに、室伏さんと武井さんが同地点から同じ方向に同時に出発した。室伏さんは分速90m、武井さんは分速65mで歩きつづけると、室伏さんが武井さんにはじめて追いつくのは2人が出発してから何時間何分後か?
では、単位変換をふくむ類題も解いてみましょう。
この類題2、求めるものは「室伏さんがはじめて追いつくのは何時間何分後か?」です。
ここですでに単位変換が必要です。
なぜなら速さが「分速○m」なので、時間の単位は「分」になおすべきだからです。
よって一行目は「室伏さんがはじめて追いつくのは \(x\) 分後とする」。
これで方程式を作っていきます。
方程式を解いたあと、出た答えをまた「何時間何分」に変換すればいい。
このように、最初の求めるものを文字でおくところから、単位は速さに合わせるというコツを忘れないで使うようにしましょう。
(単位変換の練習が必要な場合は前回の記事を参照)
次に、線分図を描きます。
この類題は反対方向に進んで出会うんじゃなくて、同じ方向に進んで1周遅れにして追いつくケースです。
だから、文章どおりに線分図を描くと、こんなごちゃごちゃしたものになります↓
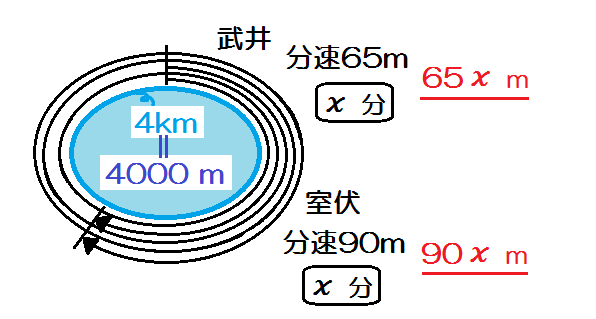
2人の線が何周もグルグルしてて、わかりにくくないですか?
ジュウゴは正直、わかりにくいです。
よってこの「同じ方向に進んで1周遅れにして追いつく」問題も、まっすぐな線で描いたらどうでしょう。
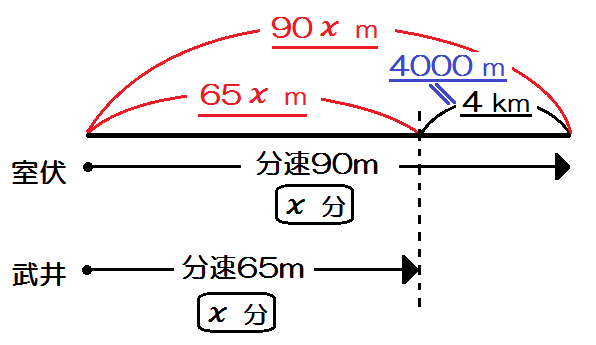
1周遅れにして追いつくということは、逆にいえば、室伏さんが武井さんよりちょうど1周分多く進むってこと。
だからこんな線分図になります。
これなら「道のり」「速さ」「時間」の3項目が3段に分かれて、すべて埋まっているか確認しやすい。
ついでに4kmという単位が速さに合ってないから、4000mに直すべきというのもわかります。
そして、等しい関係もやはり一目瞭然です。
(室伏の道のり)-(武井の道のり)=4000m だと。
$$ 90x – 65x = 4000 $$
あとは方程式を解いて、確かめて、答えを書くだけです。
\begin{eqnarray} 90x – 65x &=& 4000 \\ 25x &=& 4000 \\ x &=& 160 \end{eqnarray}
160分=2時間40分
答.2時間40分後
以上のように、「まわる問題」で同じ方向に進んで追いつく場合も、まっすぐな線分図を描くとわかりやすい。
そこから「2人の道のりの差=1周分」という方程式が立つ。
まわる問題が苦手という人、ぜひおぼえて使ってみてください。
練習問題
ここまで「まわる・出会う問題」の解き方のコツを紹介してきました。
それでは練習問題を2問用意しましたので、解いてみてください。
中学生のみならず、就活用のSPIの例題としても活用いただけます。
質問はコメント欄からどうぞ。
問3)1周400mの陸上競技場のトラックを、兄と弟がスタート地点から同じ方向に同時に走りはじめた。兄は秒速7m、弟は秒速5mで走るとすると、兄が弟にはじめて追いつくのは、走りはじめてから何分何秒後か。
問4)姉と妹の家は直線で140km離れている。姉は時速60kmの自動車で、妹の家へ向けて出発した。その15分後、妹は時速40kmの自動車で、姉の家へ向けて出発した。姉妹が出会うのは、姉が出発してから何時間何分後か。
問3)3分20秒後
問4)1時間30分後
速さが変わる問題

次に、「速さが変わる問題」を解説します。
例題3のように途中で速さが変わったり、峠をはさんで山道を進んだり、往復したりする文章問題です。
この「速さが変わる問題」もやはり、3行に分かれた線分図を描けば、文章の全体像が一瞬でわかるようになります。
解き方のコツ
例題3)かずよしくんは、自宅から1800mはなれた学校に登校するため、午前7時30分に家を出発した。最初は毎分60mの速さで歩いていたが、遅刻しそうになったので、途中から毎分100mの速さで走ったところ、午前7時56分に学校に着いた。かずよしくんが走った道のりは何mか、求めなさい。(2017 大分)
まずは「かずよしくんが走った道のりを \(x\) mとする」。
この例題は速さが「毎分○m」なので、単位変換も必要ないですね。
つづいて線分図を描いていきます。
ここまで読んだあなたなら、もう大丈夫ですね。
いちおう、丁寧に描いていくと以下のとおりです。
「かずよしくんは、自宅から1800mはなれた学校に登校するため、午前7時30分に家を出発した。」
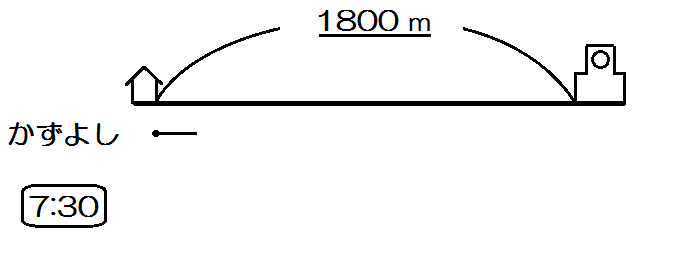
「最初は毎分60mの速さで歩いていたが、遅刻しそうになったので、途中から毎分100mの速さで走ったところ、午前7時56分に学校に着いた。」
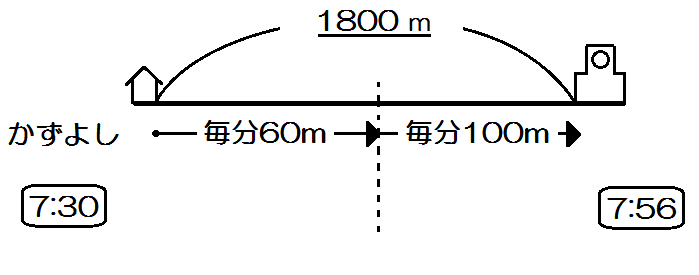
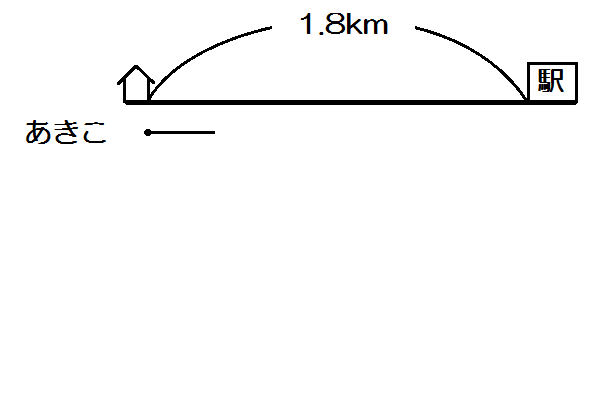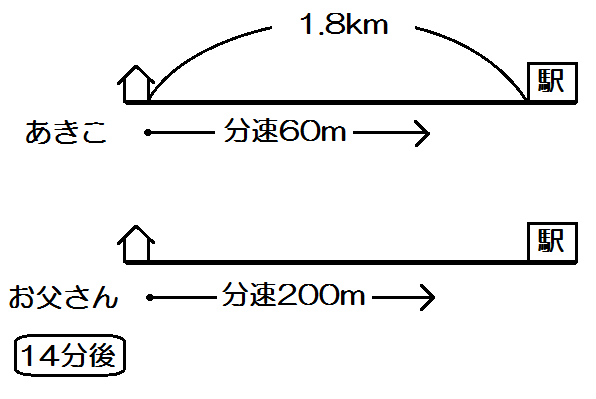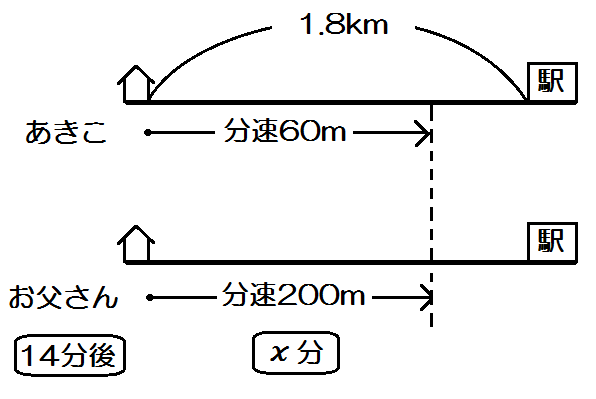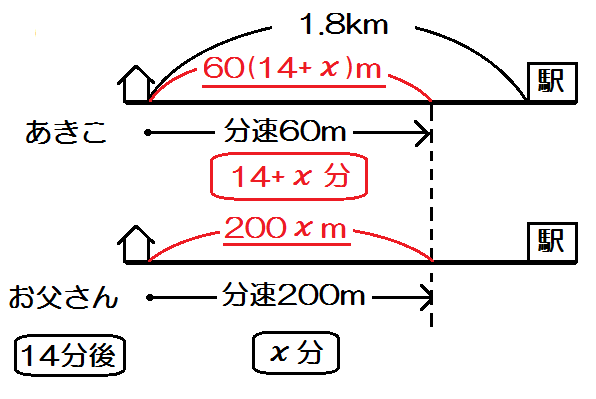
「かずよしくんが走った道のりを \(x\) mとする。」
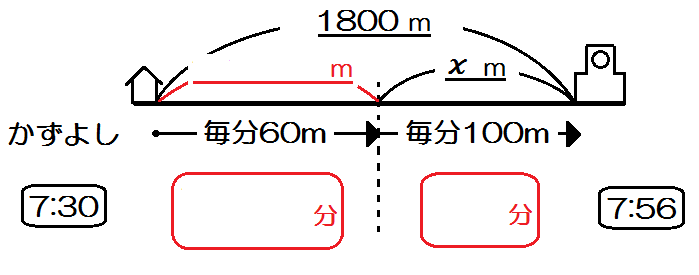
まだ埋まってないのは?そう、
「歩いた道のり」と「歩いた時間」と「走った時間」の3つ。
わかるところから \(x\) を使った式で表していきます。
3つとも埋めると、こうですね。
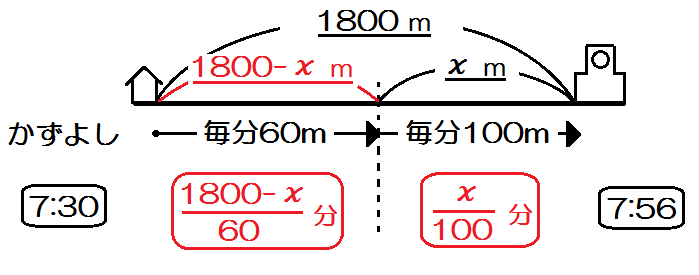
あとは方程式をつくるだけ。
7時30分に出て7時56分に着いたから、かかった時間は26分。
よって、
$$ \frac{1800-x}{60} + \frac{x}{100} = 26 $$
という方程式が立ちます。
解いて、確かめて、答えを書きましょう。
\begin{eqnarray} \frac{1800-x}{60} + \frac{x}{100} &=& 26 \\ 5(1800-x) +3x &=& 7800 \\ 9000 -5x +3x &=& 7800 \\ -5x +3x &=& 7800 -9000 \\ -2x &=& -1200 \\ x &=& 600 \end{eqnarray}
答.600m
(分数まじりの方程式が解けない・わからないという人は以下の記事を参照して復習してください)

以上のように、「速さが変わる問題」もぜんぜん難しくありません。
文章に沿って「道のり」「速さ」「時間」を3行に分けた、表のような線分図を描く。
それから3項目すべてを数字や文字式で埋めれば、方程式が立つ。
これまで紹介してきたコツを使えばすぐに解けます。
「速さが変わる問題」だからって、ちがう解き方があるわけでないのです。
単位変換を含んだ類題
類題3)家から駅まで全部で30kmある。途中のバス停までは時速5kmで歩き、バス停で16分待ち、バスに乗ってからは時速45kmの速さで進むと、家を出てから1時間28分で駅に着いた。家からバス停までの道のりは何kmか。
では最後に、「速さが変わる問題」の単位変換をふくむ類題です。
速さ・時間・道のり文章題の総まとめとして、ぜひ自分でチャレンジしてみてください。
中学生を指導している保護者さんや講師の方は、ぜひ子どもにチャレンジさせてみてください。
コツはこれですよ↓
- 文章に沿って「道のり」「速さ」「時間」を3行に分けた、表のような線分図を描く。
- それから3項目すべてを数字や文字式で埋める。
- 単位がそろっていないときは「速さ」に単位を合わせる。
・・・・・。
・・・・・・・。
では、解法例と解答です。
家からバス停までの道のりを \(x\) km とする。
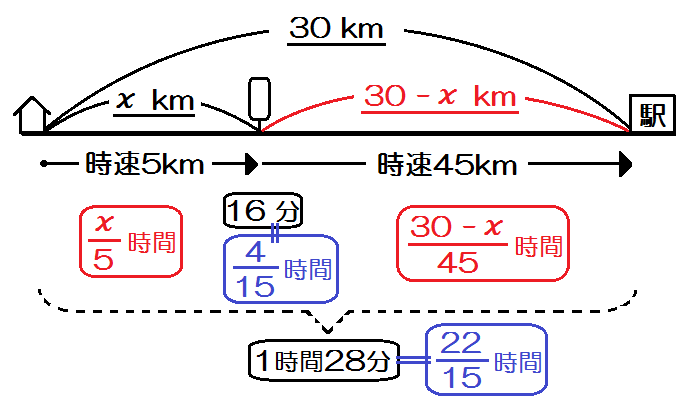
\begin{eqnarray} \frac{x}{5}+\frac{4}{15}+\frac{30-x}{45} &=& \frac{22}{15} \\ 9x +12 +30 -x &=& 66 \\ 9x -x &=& 66 -12 -30 \\ 8x &=& 24 \\ x &=& 3 \end{eqnarray}
答.3km
「16分が時間に直せない」。
「1時間28分って何時間?わからない」。
そんな場合は前回の記事の最初、「速さと単位変換の復習」を参照。
理解して、たくさん問題を解いて、ここにまた戻ってきてください。
練習問題
それでは練習問題です。
問6はすこし難問ですが、手順どおりやっていけば必ず解けます。
質問はコメント欄からどうぞ。
問5)全長17kmの山道がある。峠までの上り坂を時速3kmで歩き、残りの下り坂を時速5kmで歩いたら、ぜんぶで4時間36分かかった。上り坂は何kmか。
問6)家と図書館を往復するのに、行きは分速90mで歩き、図書館に1時間40分いて、帰りは分速60mで歩いたところ、ぜんぶで4時間10分かかった。家から図書館までの道のりは何kmか。
問5)9km
問6)5.4km
まとめ

中学数学 1次方程式文章題の「速さ・時間・道のり」問題は、
表のような線分図を描いて、3項目すべて埋めれば等しい関係がみつかる
「まわる問題」もまっすぐな線分図のほうがよりわかりやすい
単位は「速さ」に合わせる
以上、速さ問題の解き方のコツでした。
*連立方程式の道のり問題はこちら
次回は割合問題について解説します。
「原価の35%増しの利益をみこんで定価をつけたが1割引きで売ったので…」とか。
「濃度7%の食塩水200g と濃度10%の食塩水とを混ぜ合わせて…」とか。
「去年の中学校の生徒数は1200人だったが男子が20%増えて女子が15%減って…」とか。
ようするに
- 利益
- 食塩水
- 増減
この3種類の文章題の解き方のコツを解説していきます。
難問と思って苦手意識をもつ中学生も多いところですが、コツさえつかめば難しくありません。
以下のリンクからどうぞ。
[関連記事]
- 文章題①【代金、個数】
- 文章題②【分配、年齢、貯金】
- 文章題③【整数、自然数】
- 文章題④【平均の問題】
- 文章題⑤【過不足の問題】
- 文章題⑥【速さ・時間・道のり】
- 文章題⑦【速さ・時間・道のり】2
- 文章題⑧【割合の問題】
- 文章題⑨【図形の問題】
*連立方程式の道のり問題はこちら











コメント
線分図の書き方、とても参考になりました。
自分は絵が下手なので、表で説明していますが、
やはり線分図のほうが視覚的にわかりやすいですね。
授業でPCが使えるなら、取り入れたいです。
それにしても、速さの問題は、
ただでさえ「道のり・速さ・時間」が苦手な生徒が多いのに、
どうして、いきなり「追いついた」などの応用問題からはじまるんでしょう?
代金の問題では、このサイトでも、最初に、
「例題1)40円のかごに、1個80円のみかんを何個かつめたら、代金は1000円だった。みかんの個数を求めよ。」とあるように、
この程度のレベルからはじまります。
速さの問題も、これと同様に、
「家から40m歩いたあと、分速80mで走ったら、家から1000m離れた学校に着いた。何分走った求めよ。」
程度の問題からはじめたら、
まだとっつきやすいだろうに、と思います。
姉のかかった時間をx +15ではなく、妹のかかった時間をx -15にする理由はどうしてですか?
「姉が」出発してから何時間何分後か?
と問題文にあるので、
姉のかかった時間のほうをx(時間)としています。
あと単位変換が必要なので、
15(分)ではなく 4分の1(時間)ですね。
ありがとうございます!!
伊藤で41*6,45*6,57*8
か=241
こ=246
す=456
ろ=270
問6の途中式お願いします。全体の距離がわかりません
問6)家と図書館を往復するのに、行きは分速90mで歩き、図書館に1時間40分いて、帰りは分速60mで歩いたところ、ぜんぶで4時間10分かかった。家から図書館までの道のりは何kmか。
家から図書館までの道のりをx mとする。
90分のx + 100 + 60分のx =250
(1時間40分=100分)
(4時間10分=250分)
問4)姉と妹の家は直線で140km離れている。姉は時速60kmの自動車で、妹の家へ向けて出発した。その15分後、妹は時速40kmの自動車で、姉の家へ向けて出発した。姉妹が出会うのは、姉が出発してから何時間何分後か。
答.1時間30分後
これは、15分後が4分の1時間で
60x+40(x+4分の1)=140
x=10分の13=1と10分の3=1時間18分
で15分を足すと、姉妹が出会うのは1時間33分後になりませんか?
妹は15分少なく走っているので、方程式は
60x+40(x-4分の1)=140
となります。
言われてみればたしかにその通りでした
出会うわけだから追いつく場合とは意味が違ってくるんですね!
ありがとうございます!