前回のつづき。
今回は1次方程式(中学数学)の分数問題について解説します。
[前の記事]1次方程式③ かっこ、小数
[次の記事]1次方程式の文章題① 代金、個数
いきなりですが、分数のある方程式は解き方が3つあります。
①そのまま解く
②両辺に最小公倍数をかける
③両辺に公倍数をかける
どの方法でも解けるんです。
ただ①の方法だと、通分がめんどくさい。
③の方法だと数が大きくなって計算ミスしやすい。
なので、中学校はじめほとんどの中等教育では、②の方法を採用しています。
この記事でも最小公倍数をかける方法で話をすすめますが、問題によっては
「明らかに分数のまま解いたほうが速い」
「どうしても最小公倍数が出てこない」
なんて問題もあるでしょう。
そんなときは、遠慮なく①または③の方法を使ってください。
方程式ってのは、最終的に解けりゃいいんです。
数学に「この方法でなくちゃダメ」なんてないからね。

前置きはこのへんにして、本題に入ります。
分数のある一次方程式でのつまずきは、何が原因なのか?
そしてどんな具体的解決法があるのか?
4パターンに分けてみていきましょう。
(数学指導法の記事一覧はまとめページへ)
分数のある問題でつまずく
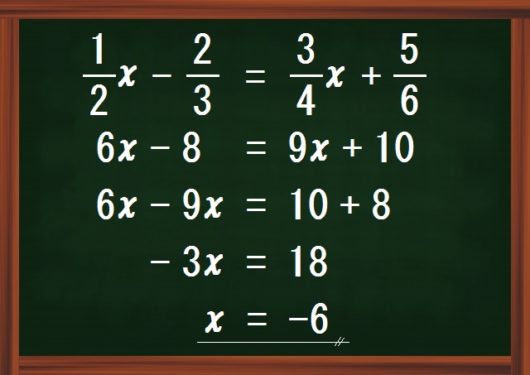
中学生が1次方程式の分数問題でつまずく原因。
それは以下の4パターンに分けられます。
- 最小公倍数がパッと出てこない
- (分数)×(整数)が暗算できない
- 項すべてに最小公倍数をかけることを忘れる
- 「分子に項2つ」の問題でかっこを付け忘れる
具体例と指導法をそれぞれ詳しく解説します。
スポンサーリンク
原因1.最小公倍数がパッと出てこない

たとえばこの問題を見て、最小公倍数が「12」とパッと出てこない。
これがつまずく原因その1です。
「これくらいなら大丈夫」という生徒は、次の問題はどうでしょうか。
$$ \frac{1}{6}x + \frac{1}{12}x + \frac{1}{7}x +5+ \frac{1}{2}x +4 = x $$
これ、有名な「ディオファントスの生涯(墓碑銘)」という問題です。
6と12と7と2の最小公倍数が「84」と、瞬時に導けますか。
「10秒以上かかった」という人は、最小公倍数に習熟していない可能性があります。
そこで、このパターンに当てはまる中学生には、最小公倍数を瞬時に導く訓練が必要です。
以下、指導案をどうぞ。
指導案
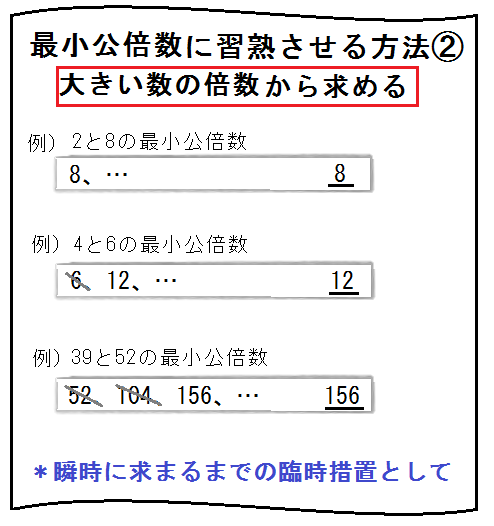
①2数の最小公倍数に習熟する
まずは2数の最小公倍数がパッと出るようにすること。
習熟方法については、「文字と式」記事でも書いたが、以下3通りがある。
最終的には、考えなくても瞬時に最小公倍数が出るようにすること。
特に「倍数を何度も書く」で2ケタ×1ケタを何度も練習させる。
数週間程度かかるが、この練習が後々生きてくる。
くわしくは「注意点」参照。
②3数以上の最小公倍数の求め方:2数ごとにやっつけていく
3数以上の最小公倍数を求めるには、手近なものから順々にやっつけていくこと。
やっつけていく順番は、自分の求めやすいものからでいい。
やり方がわかったら、てきとうな数字を出題し、練習させる。
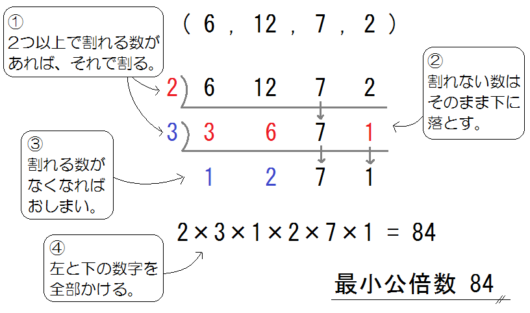
③裏ワザとして:連除法
最後に、どうしても求まらないときには、こんな裏ワザもあると伝える。
注意点
指導案①と②をすっとばして、いきなり③の連除法だけを教える。
このほうが生徒は喜ぶでしょう。
「倍数を何度も書く」という地味な反復練習もしなくて済みますからね。
しかし数学ができる子になってほしいならば、①と②をさせるべきです。
なぜなら、連除法に頼ったままでは、いつまでたってもテスト時間内に終わらないから。
そして2ケタの倍数を覚えていないと、いろんな問題でつまずくからです。
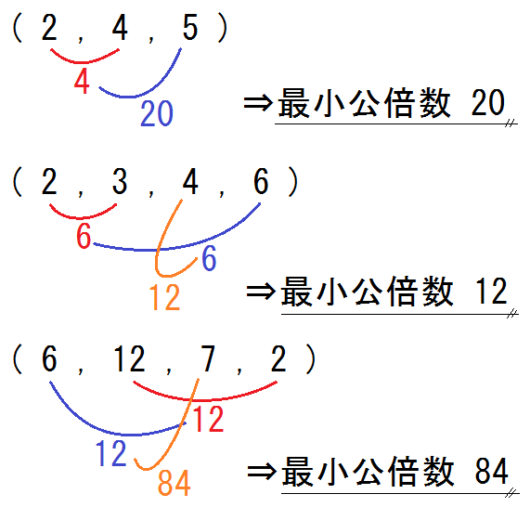
たとえば(2,3,4,6)の最小公倍数を求める場合。
これ、2数同士の最小公倍数がパッと出る生徒なら、パッパッパと「12」と出てきます。
しかし連除法でしか求められない生徒は、横に連除法を書いて、30秒くらいかかるはずです。
このスピードの差が、テスト時間内に収まるかどうかの分かれ目になります。
「やれば絶対にできた、でも時間内に最後までいかなかった」。
こんな生徒を、そのままにしておくのか。
それとも、時間内に解けるような暗算力をつけてあげるのか。
指導案①と②をさせるかどうかは、ここの差になってくるのです。
また、指導案①では2ケタの倍数も書かせますが、これは以下のような問題を解けるようにするためです。
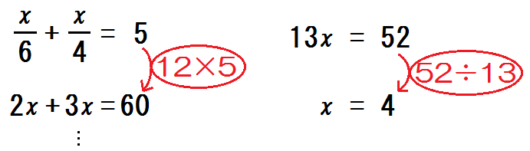
これらは1次方程式だけに限った例です。
ほかにも様々な単元で、この先2ケタ×1ケタや2ケタのわり算の計算が、当たり前のように出てきます。
「ちょっと数が大きくなると、すぐできないってなる」。
「2ケタの数字が出るたびに、横に筆算を書いている」。
いつまでもこの状態でいさせるか。
それとも、数学ができる喜びを味わわせてあげるのか。
安易に連除法に頼るかどうかは、ここの差にもなるんです。
というわけで、倍数の並びを身につけて最小公倍数がパッと出るようにしてあげる方法を、私はおススメします。
原因2:(分数)×(整数)が暗算できない

最小公倍数「12」は出たけど、(分数)×(整数)の計算が頭の中でパッとできない。
これが分数の方程式でつまずく原因その2です。
当ブログでは、ここでつまずかないために、「文字と式」段階で暗算できるようにする指導をおススメしています↓

ただ(分数)×(整数)が暗算できないまま、ここまで来てしまった中1もいるでしょう。
そういう中学生のための指導法は、以下のとおりです。
指導案
①小6(分数)×(整数)問題の復習
小6「分数のかけ算」のドリルなどを用意して、(分数)×(整数)の問題を示す。
$$ \frac{5}{6} \times 12 $$
ここで、約分の\を書かずにさせること。
難しければ、約分後の数を頭の中に保持するよう指導すること。
つまりこう。
先生「\(6\) と \(12\) で約分、上に何が残る?」
生徒「\(2\)」
先生「\(5 \times 2\) ?」
生徒「\(10\)」
$$\frac{5}{6} \times 12 = 10 $$
これを自力でパッとできるまで、くりかえさせる。
②項をひとつずつ暗算させる
以下のような問題を示し、横にちいさく最小公倍数を書く。
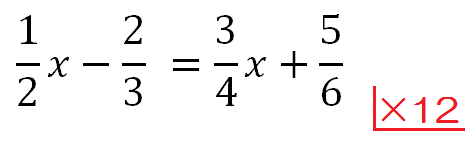
発問していき、項をひとつずつ計算させる。
先生「\( \frac{1}{2}x \times 12\) ?」
生徒「\(6x\)」
先生「\(-\frac{2}{3} \times 12\) ?」
生徒「\(-8\)」…↓
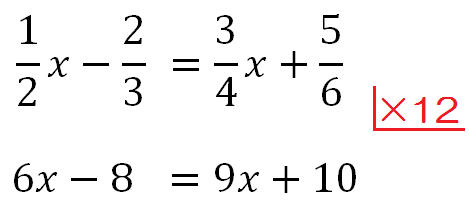
③練習
同様の問題を目の前で解かせたのち、自分でできるようになるまで練習させる。
なお、分母をはらったあと、方程式を最後まで解かせるかどうかは生徒の力量による。
方程式の基本計算がバッチリの子であれば、分母をはらうだけでいい。

注意点
②③の段階で、\(x\) をつけ忘れたり符号をまちがえたりする。
そんな生徒には、「符号→数字→文字」の順でこまかく決定させるといいでしょう。
教え方は、前回の記事中の「分配法則」で書いたものと同様です。

また、横にちいさく最小公倍数を書かせる指導は、まちがえなくなれば止めてかまいません。
逆にいえば、生徒が分母をはらう計算に慣れるまでは、書かせたほうがいいでしょう。
そしてこの「横にちいさく最小公倍数を書く」指導は、次の「項すべてに最小公倍数をかけることを忘れる」場合でも役立ちます。
原因3:最小公倍数のかけ忘れ

このように、項すべてに最小公倍数をかけることを忘れてしまう。
特に分数項と整数項のまじった方程式だと、整数項にもかけるということを忘れる。
これがつまずきの原因その3です。
このパターンの計算ミスをする生徒には
- 横にちいさく最小公倍数を書かせる
- 項すべてに下線を引く
という指導が有効です。
指導案
①何倍するか、横に書かせる
方程式の横に、「×(最小公倍数)」と書く。
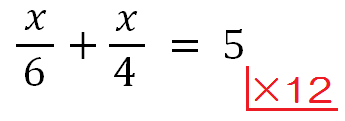
②項すべてに下線を引く
項すべてに下線を引く。
そして「項すべてに \( \times12\) する」と伝え、発問していく。

先生「\( \frac{x}{6} \times 12\) ?」
生徒「\(2x\)」
先生「\( \frac{x}{4} \times 12\) ?」
生徒「\(3x\)」
先生「\( 5 \times 12\) ?」
生徒「\(60\)」
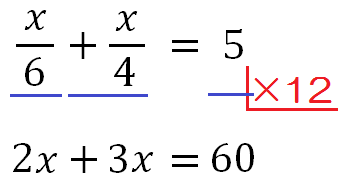
③練習
できるようになるまで練習。
最後まで解かせるかは、おなじく、生徒の力量をみて。
注意点
この指導案は、前回の記事で書いた「小数:10倍、100倍…忘れのミス」における指導とまったく同じです。
前回同様、生徒自身が横に書く、生徒自身が下線を引く、というように導いてあげてください。
こうした補助を書くのは間違えなくなるまで、という点でも同じです。
また、見てわかるとおり、\(12 \times 5 \) が暗算でできる必要があります。
つまりここでも、2ケタ×1ケタ(や2ケタのわり算)の暗算力が求められるのです。
そして、「原因2:(分数)×(整数)が暗算できない」に当てはまる生徒の場合もまた、2ケタ×1ケタ(および2ケタのわり算)の暗算力はあったほうがいい。
それは、「ディオファントスの生涯(墓碑銘)」問題を解くことを考えればわかります。
$$ \frac{1}{6}x + \frac{1}{12}x + \frac{1}{7}x +5+ \frac{1}{2}x +4 = x $$
この問題を解くには、以下の計算を頭の中でしなければならないからです。
\begin{eqnarray} & &84\div6 \qquad 84\div12 \qquad 84\div7 \\& &84\times5 \qquad 84\div2 \qquad 84\times4 \end{eqnarray}
ということは、分数のある方程式がわからない・できない。
その根っこには、2ケタ×1ケタ(および2ケタのわり算)の暗算力不足がある。
だから、たとえ連除法で最小公倍数が機械的に出せるようになっても、たとえ1ケタ同士の(分数)×(整数)が暗算できるようになっても、たとえ方程式の横や下に補助を書いてかけ算忘れがなくなっても、いまだ分数の方程式が苦手である…。
そんな生徒にはやはり、上で書いたように、2ケタ×1ケタの練習が必要なんです。
もういちど言います。
安易に連除法に頼らせないで、倍数の並びを身に付けさせてください。
結果として、それが一番の近道です。
原因4:「分子に項2つ」の問題
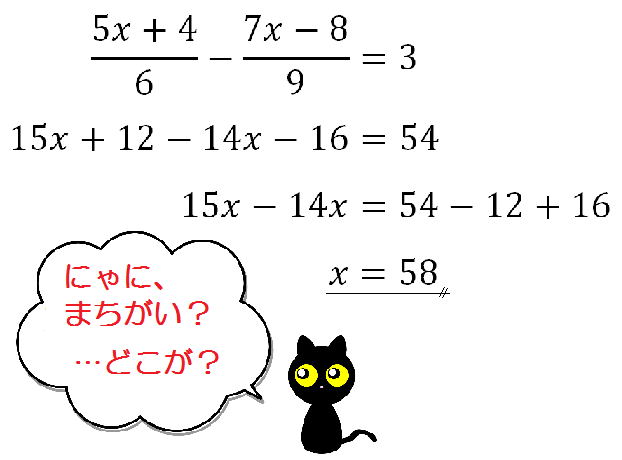
さて、ここまでが分数方程式の基本です。
最後はすこし応用範囲になります。
上図のような「分子に項が2つある」分数の方程式。
これ、中学2年生で本格的に学びますが、発展課題として中1で出てくることもあります。
ここで、図のような計算ミスが多発します。
そのような生徒には、分母をはらったあとに必ずかっこを付けることを徹底させましょう。
指導案
①正しい解法でやってみせる
分子に項2つの方程式では、分母をはらったあと、必ずかっこを付けると伝える。
そのうえで、以下のように正しい解法を示す。
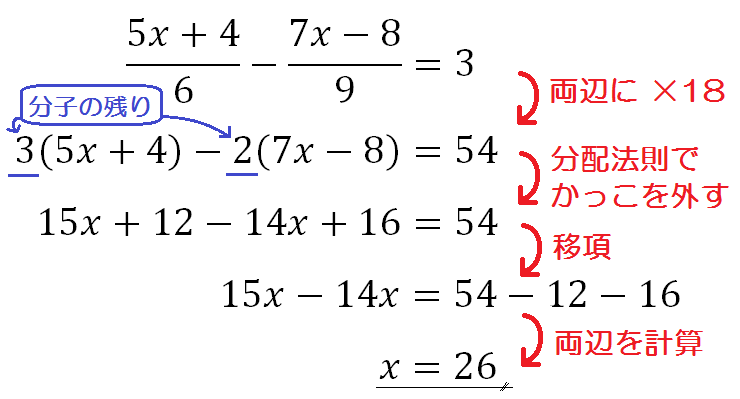
②目の前でさせてみる
類題を出して、目の前で解かせる。
\begin{eqnarray} \frac{4x-5}{2}- \frac{5x-7}{3} &=& \frac{1}{8} \\ \frac{3x-2}{4}+ \frac{7x+8}{9} &=& \frac{x+5}{6}- \frac{10x-11}{12} \end{eqnarray}
(解は順に \(x=\frac{7}{8}\) 、\(x=\frac{49}{79}\) )
③練習
まちがえなくなるまで、練習。
注意点
なぜかっこを付けたままにするべきか?
その理由は、以下のとおりです。
疑問に思う生徒には、以上の内容を伝えてあげてください。
また、②の類題として出した問題のふたつめ。
$$ \frac{3x-2}{4}+ \frac{7x+8}{9} = \frac{x+5}{6}- \frac{10x-11}{12} $$
これくらいの問題がサッと解けたら、「数学ができる」部類に入りますね。
この問題が解けるためには、
- 4と9と6と12の最小公倍数が「36」と瞬時にひらめく
- \(36\div12=3\) と瞬時に暗算できる
- \(79x=49\) まで来たときに「79と49の公約数はない」と瞬時に思える
こうした暗算力が必要です。
そしてそのためには、少なくとも11~19の倍数が頭に入っている。
つまり2ケタ×1ケタの答えをだいたい覚えてるという状態が必要なんです。
前々回の記事で、中1段階における中学数学でのつまずきは、おおもとの原因を突き詰めていくと、途中式を書く習慣がないことと計算力不足の2つだと書きました。
このうち計算力不足は、鍛えることで解消できます。
鍛えるとはつまり、反復練習をおこなって神経回路を強化し、正しい行動を即座にアウトプットできるようにすることです。
3回目ですが、しつこいくらい言います、
倍数の並びを身につけさせて。
まとめ

分数のある1次方程式でつまずく原因は4つ。
1.最小公倍数がパッと出てこない場合…
- まず2数の最小公倍数に習熟する。
倍数を何回も書き、数の並びから身につけること。 - 3数以上は、2数ごとにやっつけていく。
順番は自分の求めやすいものからでいい。 - 連除法は、裏ワザとして教える。

2.(分数)×(整数)が暗算できない場合…
- 小6「分数のかけ算」に習熟する。
約分後の数を頭の中に保持して暗算すること。 - 横にちいさく、何倍するかを書く。
- 項をひとつずつ暗算していく。
「符号→数字→文字」の順でこまかくやってもいい。
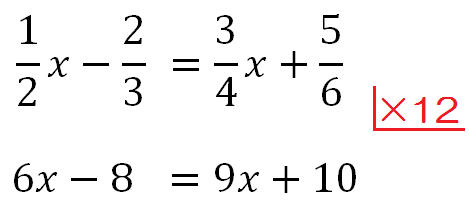
3.整数項に最小公倍数をかけ忘れる場合…
- 横にちいさく、何倍するかを書く。
- 項すべてに下線を引く。
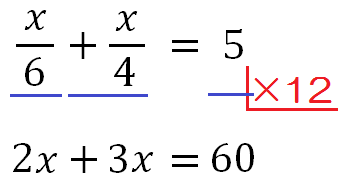
4.「分子に項2つ」でつまずく場合…
- 分母をはらった後も、かっこを付けたままにすること。
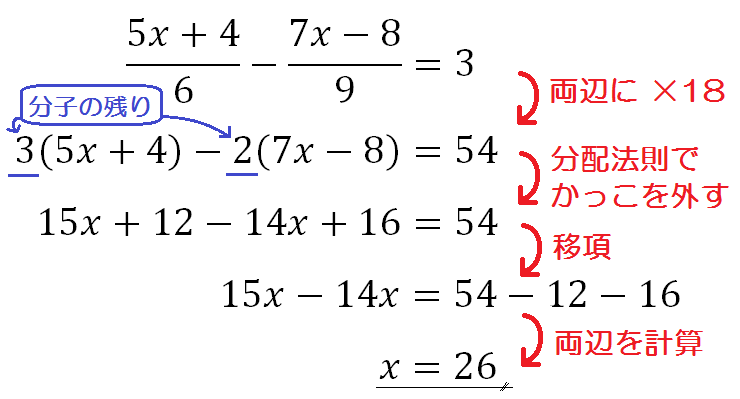
*それでも「分数にがて」という生徒は、2ケタ×1ケタの暗算力不足。
この機会に、倍数の並びを何回も練習して、2ケタ×1ケタ(と2ケタのわり算)を暗算できるようにすべき。
さて、中1数学「1次方程式」計算単元における解説は以上です。
次回からは文章題に入ります。
文章問題ができない…
どこから手をつけていいか、解き方さえわからない…
そんなつまずきに対しての解消法をお教えします。


















コメント
2ケタ×1ケタの計算、
数学が平均点以上の子でも、
暗算でできない生徒が多いですね。
今まで、時間がもったいないと思いつつ、
よい指導法がなく、手をこまねいておりましたが、
「倍数を何度も書く」を試してみようと思います。
このサイトに書いてある例題ではないのですけど、もし良ければ教えてもらいたいです。
円錐の表面積を求める問題のなかで方程式が出てきて、解き方の流れは書いてあって全体の意味はわかるのですけど途中計算が詳しく書かれていないので細かいところがわかりません。
解法の一部をそのまま載せます
『展開図のおうぎ形の弧の長さは、底面の円周に等しいから、
おうぎ形の中心角をX°とすると
2π×26×360分のX=2π×10
これより、360分のX=26分の10=13分の5となって』
これの、2π×26×360分のX=2π×10がなぜ13分の5になるのかいまいちわかりません。
Xが13分の5なのか?それともXを求めてそれを約分したものが13分の5なのか?だとしたらXはどう求めるのか?がよくわかりません。
良ければ途中計算を解説してもらえないでしょうか?
はるさんへ
「2π×26×360分のX=2π×10」
両辺を2πでわって(両辺に2π分の1をかけて)
「26×360分のX=10」
両辺を26でわって(両辺に26分の1をかけて)
「360分のX=26分の10」
あとは右辺を約分すると
「360分のX=13分の5」
となります。
ちなみにそのあとは、両辺に360をかけて
「X=13分の5 ×360」
んで、さいご、右辺を計算して
「X=150」ですね。