中1数学 1次方程式の文章題。
6,7回目は「速さ・時間・道のり問題」の解き方のコツです。
速さの文章問題がどうも苦手…
どう方程式を立てたらいいかわからない…
ここで数学が嫌いになった…
こんな中学生に活用ください。
また例題・類題もたくさん設けたので、就活生のSPI用の復習としても使えます。
「速さ・時間・道のり問題」が苦手になる原因は、大別すると2つです。
- 内容の全体像がつかめない
- 速さや単位変換への苦手意識
つまり文章が長くてつながりがわからず、何を言ってるのか頭がこんがらがってしまう。
またそもそも、「分速60m」とかイメージできないし、「1時間23分は何時間か」と言われるとそれだけでイヤになる。
こうした2つの理由があわさって、速さの文章題を解けなくしているのです。

そこでこれらの原因を解決するために、この記事では3つの解決法を示します。
- まず速さや単位変換の問題を復習する
- ここで紹介する方法で線分図を描いてまとめる
- 単位がそろってないときは単位を「速さ」に合わせる
1.でまず、速さという概念や単位変換にたいする苦手意識を払拭します。こうした苦手意識が芽生えるのは、速さとは何かの理解があいまいなまま「み・は・じ」とかの公式を覚えさせられたこと、そして単位変換や速さを求める基本問題の練習不足に起因しています。よって、方程式文章題に入る前に、小学校でやった速さの学習を復習すべきなんです。
2.はこの記事のミソ。つまり「速さ・時間・道のりの方程式文章題」の解き方のコツとなります。文章が長くてつながりがわからない、全体像が見えなくなるという原因をイッパツで解決し、内容全体がすっきり整理できるような線分図を、ここで紹介します。この線分図さえ自分で描けるようになれば、どんな文章題でも方程式をつくることができるようになります。
3.は「速さ文章題」におけるもうひとつのコツです。知らない中学生も多いので、やはりここで紹介していきます。
この3つの解決法を知ることで、過去何百人という中学生が「速さの問題もダイジョウブ!」になっていきました。
このノウハウをぜひ、ひとりでも多くの人に知ってもらいたいと思います。
ではいきましょー。
(速さの理解や単位変換は問題ないという場合は、最初の大見出しをスルーして2つめの「追いつく問題」に飛んでください)。
速さと単位変換の復習

速さ・時間・道のりの求め方がすぐに出てこない…
1時間23分は何時間か、変換できない…
そもそも速さっていう概念がよくつかめていない…
こうなる原因は先述したとおり、2つあります。
ひとつは速さとは何かの理解がぬけたまま公式だけ覚えさせられたこと。
そしてもうひとつは練習が不十分であることです。
そこでこのような生徒はまず、実際の方程式文章題に入る前に、以下5段階にわけて速さと単位変換の復習をするとよいでしょう。
- 速さとは何か理解する
- そこから公式が導かれることを知る
- 速さ・時間・道のりを求める練習
- 単位変換の練習
- 単位変換をふくんだ速さ・時間・道のりを求める練習
以下、実際の指導例です。
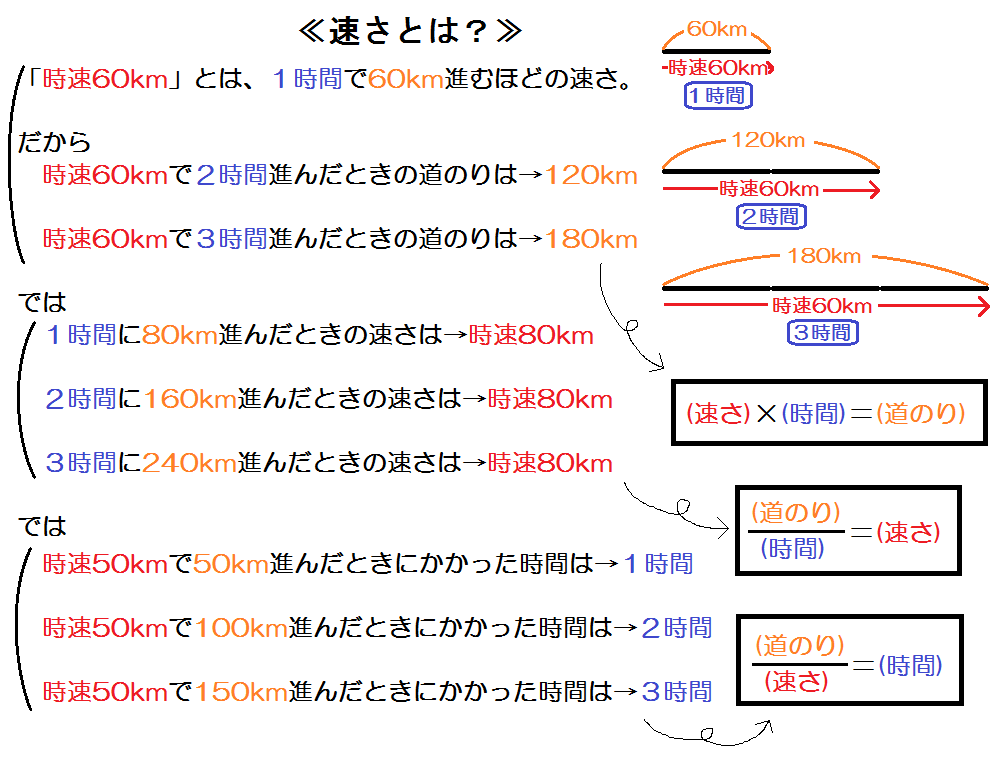
速さとは何か、速さの公式
速さとは「単位時間あたりに進んだ道のり」のこと。
単位時間とは1時間、1分、1秒など。
つまり、こういうかんじ。
これを見れば、速さとは何かも、そこから3つの公式が導かれることもわかるね。
分速や秒速も、同様です。
公式や「み・は・じ」「は・じ・き」だけ覚えている中学生は、まずこの説明を理解して。
そうしたらもう、速さ・時間・道のりの求め方を忘れることはないよ。
*この解説図は子どもにとってつまずきやすいポイントを押さえたものになっています。詳細は省きますが、速さが時間・道のりとは別の独立したスカラー量であること、線分図でイメージを助けることなど、工夫してこういう形にしています。よってもしご利用の場合、この図はこのままコピーしていただいてかまいません。
速さ・時間・道のりを求める練習
じゃあ、次の問題を解いてみよう。
*これらの問題も中学生になってつまずきやすい個所をカバーするよう、工夫した問題・配列にしています。このままコピーorダウンロードしてお使いいただいてかまいません。
単位変換と、単位変換を含んだ練習
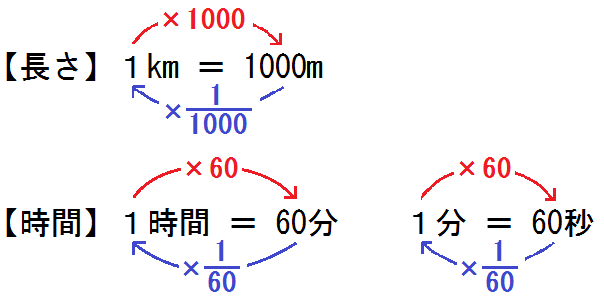
次に単位変換の復習をしよう。
「時間」と「道のり」の単位変換は、以下のようにするんだった。
だから、6kmは \(6 \times1000\) で6000m。
180分は \(180 \times \frac{1}{60}\) で3時間。
ついでに時速30kmは時速30000mで、分速500mだ。
以下、単位変換の復習問題を解いてみよう。
最後に、単位変換を含んだ速さ・時間・道のりの問題を復習しよう。
ここまでが小学校で習った範囲。
これが解けたら、いよいよ中学の方程式文章題に入っていくよ。
→無料プリントサイト「無料で使える学習ドリル 速さの基本・単位変換」
*作成がめんどうになったいい無料プリントサイトがあったのでこちらをどうぞ。
*上に掲載の単位変換問題もご自由にお使いください。
追いつく問題

それではいよいよ、中学数学の方程式文章題「速さ・時間・道のり問題」をやっつけていきます。
- 追いつく問題
- まわる・出会う問題
- 速さが変わる問題
速さの文章問題には大きく分けてこの3種類がありますが、解き方はひとつ、つまりマスターすべき最大のコツはたったひとつです。
それは表のような線分図を描くこと。
これさえ描けるようになれば、どんなに長くて複雑な文章もバッチリ整理できるようになります。
解き方のコツ
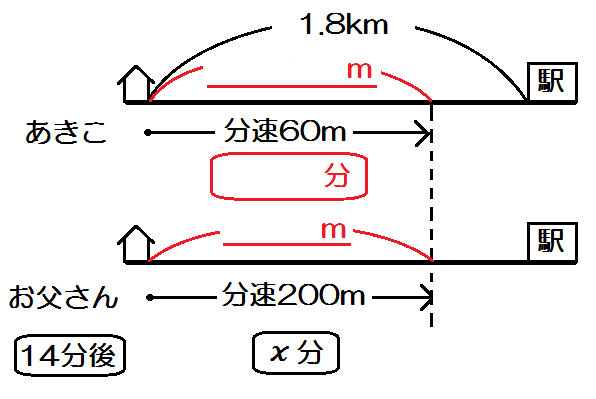
例題1)あきこさんは、1.8km離れた駅に向けて家を出発した。それから14分後に、お父さんは自転車で家を出発し、同じ道を通って駅に向かった。あきこさんは分速60m、お父さんは分速200mでそれぞれ一定の速さで進むとすると、お父さんが家を出発してから何分後に追いつくか、求めなさい。(2017 千葉 前期)
まず求めるものを \(x\) とします。なので一行目は、
「お父さんが家を出発してから \(x\) 分後に追いつくとする」。
次に、文章に沿って線分図を描いていきます。
どのように描けばいいのか?
百聞は一見に如かず、このように描きます。
「あきこさんは、1.8km離れた駅に向けて家を出発した。」
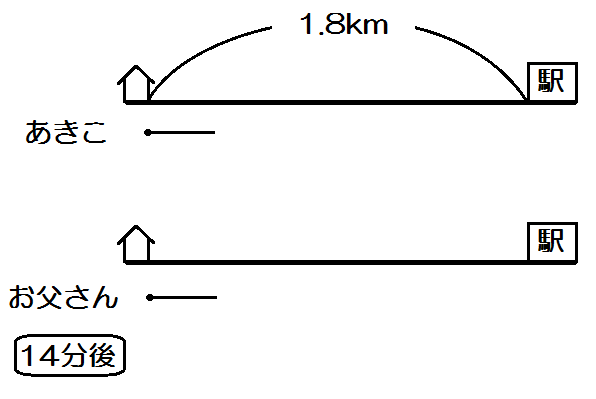
「それから14分後に、お父さんは自転車で家を出発し、同じ道を通って駅に向かった。」
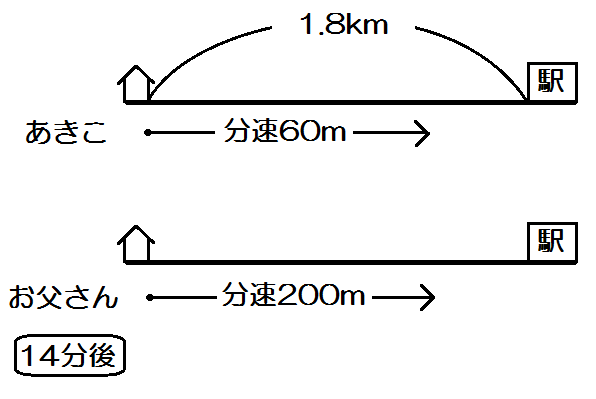
「あきこさんは分速60m、お父さんは分速200mでそれぞれ一定の速さで進むとすると、」
「お父さんが家を出発してから \(x\) 分後に追いつく。」
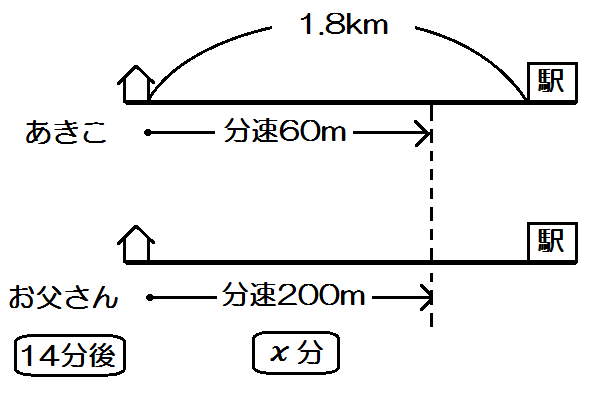
このように、「線の上」「線のすぐ下」「さらに下」と3段に分けて、それぞれ道のり・速さ・時間をどこに書き込むか決めておくのです。2人いるなら2本の線を引いて、それぞれ3段を埋めていくのです。
ジュウゴの場合は上から「道のり」「速さ」「時間」と決めて教えていますが、どこに何を書くと決めてもかまいません。
とにかく、「線の上に書き込むのは道のり」等と決めて、それをやぶらない。
これがきれいでわかりやすい線分図を描くコツになります。
ここまで描けたら、次にまだ埋まっていない箇所を埋めていきます。
まだ埋まっていない箇所は3つ。
あきこの「道のり」と「時間」、そしてお父さんの「道のり」です。
*埋まっていない箇所が見つからないという場合は、以下のような表を書いてもいいですが、慣れてきたら線分図だけで事足りるようになります。
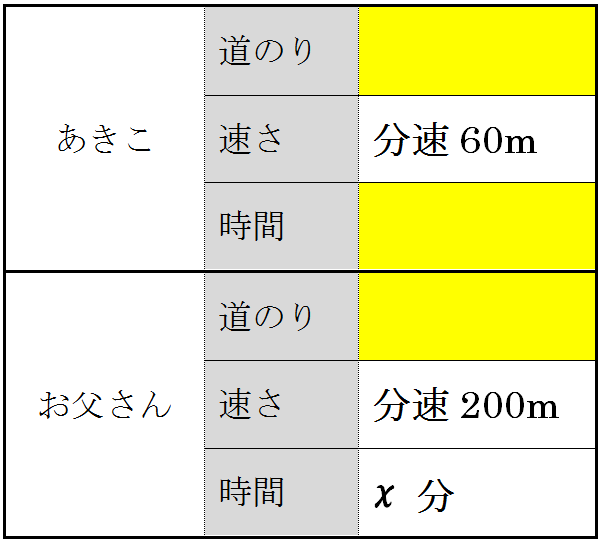
この埋まっていない3つを、わかるところから、\(x\) を使った式で表していくんです。
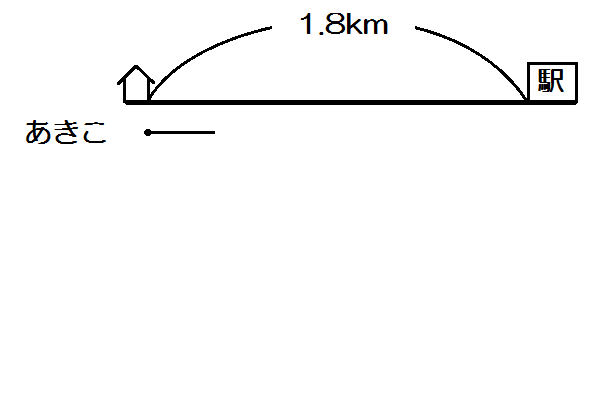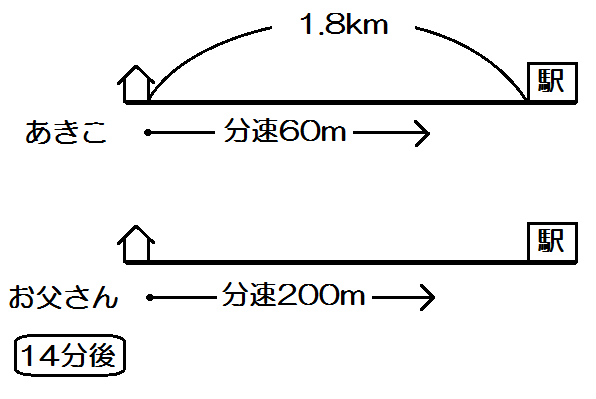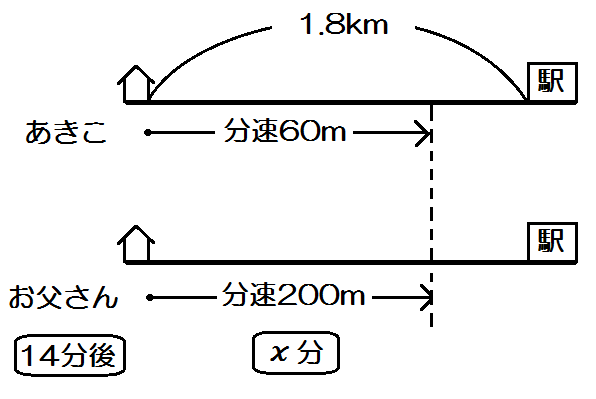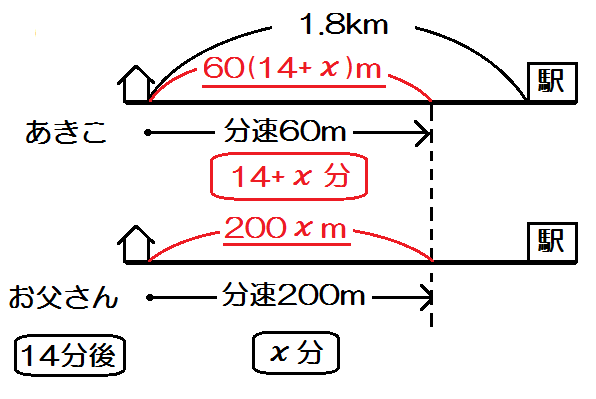
まずあきこの「時間」。お父さんより14分多く歩いているんだから、\(14+x\) 分ですね。
またお父さんの「道のり」。速さ×時間=道のりだから、\(200x\) mですね。
そしてあきこの「道のり」。速さ×時間=道のりだから、\( 60(14+x) \) mですね。
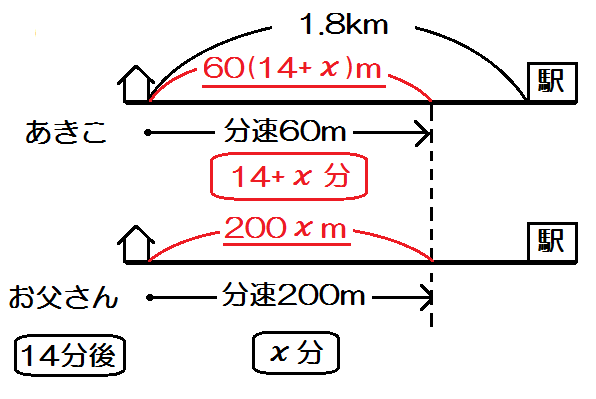
こうして「道のり」「速さ」「時間」の3項目をすべて書き込む。
数字や、\(x\) を使った式で、ぜんぶ埋める。
そうしたらあとは等しい関係を見つけるだけです。
「追いつく問題」ではたいてい等しい関係は決まってます、道のりです。
つまり「あきこの道のり」=「お父さんの道のり」。
よって方程式は
$$ 60(14+x) = 200x $$
以上のように、
- 線分図を「道のり」「速さ」「時間」の3段にわけてきれいに描く
- 埋まっていない箇所を数字や文字式でぜんぶ埋める
この手順で、必ず方程式ができるのです。
もういちど、線分図の描き方をアニメーションでまとめてみました。問題と照らし合わせながら、どのように作っていくのかイメージしてください。
ちなみに例題1を最後まで解くと次のとおりです。
解)お父さんが家を出発してから \(x\) 分後に追いつくとする。
\begin{eqnarray} 60(14+x) &=& 200x \\ 840+60x &=& 200x \\ 60x-200x &=& -840 \\ -140x &=& -840 \\ x &=& 6 \end{eqnarray}
答.6分後
単位変換をふくんだ類題
類題1)黒田さんは分速70mで、事務所から2km離れたスタジオに向かった。0.2時間後に、小淵さんが分速130mで同じ道を追いかけた。小淵さんが黒田さんに追いつくのは、小淵さんが事務所を出てから何分後か。また、それはスタジオの何m手前の地点か。
さて、同様の追いつく問題、今度は単位変換をふくむ類題を解いてみましょう。
上とおなじ手順でいきます。
最初にまず「小淵さんが事務所を出てから \(x\) 分後に追いつくとする」。
これはいいですね。
スタジオの何m手前の地点かも求めよと書いてありますが、とりあえず置いときます。
次に、文章に沿って線分図を描いていきます。
ぜひ自分でチャレンジしてみてください。
どうですか?
できましたか?
おそらく「0.2時間後」という数字でハタと止まったはずです。
単位を変換しなければならない、と。
ここで、おぼえておいてほしいもうひとつのコツがあります。
単位は速さに合わせるとラク。
いま、速さの単位は「分速○m」なので、0.2時間を分に変換するんです。
はい、12分ですね。
また2kmもmに変換します。
そう、2000mですね。
(この単位変換ができないという人は上の復習をしてからここに戻るべし)
こうして、速さに単位をそろえて線分図を完成させます。
ジュウゴなら、こう描きます。
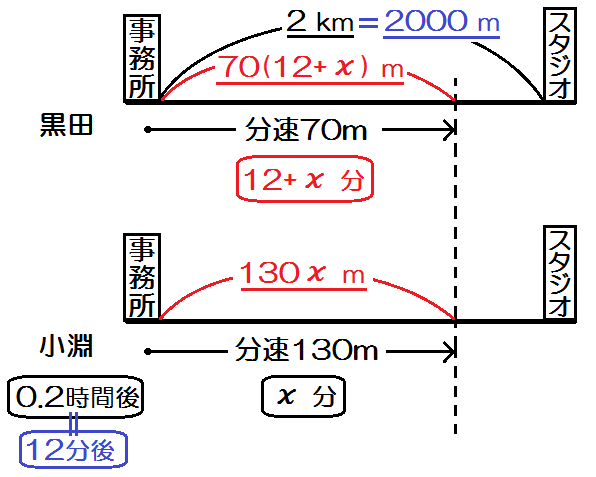
よって方程式は
\begin{eqnarray} 70(12+x) &=& 130x \\ 840+70x &=& 130x \\ 70x-130x &=& -840 \\ -60x &=& -840 \\ x &=& 14 \end{eqnarray}
答.14分後
と出ます。
また、追いついたのはスタジオの何m手前の地点か、という設問もあるので、
\(70(12+x) \) に \(x=14\) を代入して、あるいは
\(130x \) に \(x=14\) を代入して、\(1820\) (m)。
\(2000-1820=180\) 。
答.180m手前の地点
と出ます。
以上のように、単位変換が必要な文章題では、単位を速さに合わせるとおぼえておきましょう。
*ちなみに例題1にも「1.8km」と速さに合ってない単位がありましたが、問題に関係なかったのでそのままでした。問題で使わない数字が出てくる方程式文章題も、たまにあります。使うか使わないかは、線分図を描けばやっぱりわかりますよ。
練習問題
単位変換はなぜ、速さに合わせるのか?
それは速さの変換が一番ややこしいからです。
時間や道のりの変換のほうがラクなので、速さに合わせたほうが効率的なんです。
だから「時速○km」だったら、時間は「□時間」に、道のりは「△km」に合わせる。
「秒速○m」だったら、時間は「□秒」に、道のりは「△m」に合わせる。
このコツをぜひ活用して、できるだけ効率的に解いていってください。
では、「追いつく問題」の練習を2問、用意しました。
○「道のり」「速さ」「時間」の3段にわかれた線分図を描く
○埋まっていない箇所を数字や文字式でぜんぶ埋める
○単位変換は速さに合わせる
以上3つのコツを使ってやっつけてみてください。
解答は末尾に記載、質問はコメント欄からどうぞ。
問1)子どもが8時に、家から体育館へ向けて走りはじめた。20分後に、子どもの忘れものに気づいた母が自転車で追いかけた。子どもの速さを分速120m、母の速さを分速270mとすると、母は何時何分に子どもに追いつくか。
答.8時36分問2)目的地までちょうど100kmある一直線の道路を、Aがスクーターで出発した。1時間10分後、Bがバイクで同じ道を追いかけた。Aの速さを時速30km、Bの速さを時速55kmとすると、Bは出発してから何時間何分後にAに追いつくか。また、それは目的地から何km手前か。
問1)8時36分
問2)1時間24分後、23km手前
*連立方程式の道のり問題はこちら
とりあえずのまとめ
記事が長くなったのでいったんまとめます。
中学数学の方程式文章題「速さ・時間・道のりの問題」。
解き方のコツは以下のとおりです。
<速さや単位変換に苦手意識がある場合…>
次の5段階にわけて、まず小学校の内容を復習する。
- 速さとは何か理解する
- そこから公式が導かれることを知る
- 速さ・時間・道のりを求める練習
- 単位変換の練習
- 単位変換をふくんだ速さ・時間・道のりを求める練習
特に、速さとは何かあいまいなまま「み・は・じ」等の公式を覚えさせられた人。
また、1時間23分が何時間かパッと単位変換できない人。
こんな中学生は、方程式文章問題に入る前にかならず復習をして、苦手意識を払拭すること。
SPIの速さ問題が苦手な就活生も同様です。
<文章を読んでも方程式が作れない場合…>
次の2段階にわけて、表のような線分図を描く。
- 文章に沿って「道のり」「速さ」「時間」の3段にわけて書き込んでいく
- 埋まっていない箇所を数字や文字式でぜんぶ埋める
特に、文章が長くなると全体像が見えなくなるという人。
また、線分図を描くように指導されたけど、いまいち描き方がわかってなかった人。
こんな中学生こそ、「道のり」「速さ」「時間」をきれいに書きわけた、表のような線分図を描くべきなんです。
<単位変換をふくんだ文章題になると難しい場合…>
単位はすべて速さに合わせること。
文章に「分速○m」とあるなら、時間は分に、道のりはmにそろえる。
文章に「時速○km」とあるなら、□時間に、△kmにそろえる。
それがいちばん効率的。
なお、単位変換自体が苦手という場合は小学校の単位変換問題をたくさん練習して、もう大丈夫になってから、文章問題にとりかかること。
さて、記事中で方程式文章題の速さ問題には
- 追いつく問題
- まわる・出会う問題
- 速さが変わる問題
の3種類あると言いました。
次回は「まわる・出会う問題」と「速さが変わる問題」をやっつけます。
解き方は変わりません。ここで紹介した方法がこれらの問題にも適用できることを示していきます。
→中学数学「1次方程式」文章題の解き方⑦「速さ・時間・道のり」その2
[関連記事]
- 文章題①【代金、個数】
- 文章題②【分配、年齢、貯金】
- 文章題③【整数、自然数】
- 文章題④【平均の問題】
- 文章題⑤【過不足の問題】
- 文章題⑥【速さ・時間・道のり】
- 文章題⑦【速さ・時間・道のり】2
- 文章題⑧【割合の問題】
- 文章題⑨【図形の問題】
*連立方程式の道のり問題はこちら












コメント
練習問題2のどうしてXが5\7になるのかが分かりません、
練習問題の問2の解説をお願いします。
Bは出発してからx時間後にAに追いつくとする。
30(x+ 7/6) = 55x
これを解いてx=7/5
7/5時間=84分=1時間24分
あとは下の返信のとおりです。
質問失礼します
練習問題(2)の何時何分にAに追いつくかの方は解けたのですが
目的地から何km手前か、の解き方が分かりません。
x= 7/5(5分の7) 時間後と出たなら、
それを方程式の左辺または右辺に代入します。
どっちであっても77になるので、
100-77=23(km)
と、目的地から23km手前と答えが出ます。
速さ問題を
•追いつく問題
•まわる・出会う問題
•速さが変わる問題
の3つに大別されていますが、
上の2つは、
・追いつく問題
・出会う問題
・差がつく問題
に分類した方がよいかと思います。
まわる問題は、出会う問題や差がつく問題のバリエーションにすぎないからです。
(出会う問題や差がつく問題は、いきなりまわる問題でやらせるのではなく、まずは直線上でやらせた方がいいでしょう)
そして、速さ問題の難しさは、
ご指摘のとおり、「速さや単位変換への苦手意識」はもちろんですが、
過不足の問題と同様、等しい関係が問題文に明示されていないことにあると考えます。
そのため、上記のように3つに分け、
・追いつく問題では、(Aの道のり)=(Bの道のり)
・出会う問題では、(Aの道のり)+(Bの道のり)=(AB間の距離)
・差がつく問題では、(Aの道のり)-(Bの道のり)=(ABの差)
となることを理解させ、覚えさせる、
これが重要だと考えます。
いろいろと勉強になります。
ありがとうございます。
毎回、分かりやすい説明でありがたい限りです。
ただ、iPhoneやiPadでは練習問題の解答を見ることができないのが残念です^^;
(「一行下をドラッグ反転で見る」ことができない)
これは不注意でした、知りませんでした。
随時、「末尾に小さく記載」に訂正していきますね。
ありがとうございます!
おかげで、印刷して子供に自習させることができるようになったので、非常に便利になりました!
というか、じゅうごさん、これ出版しませんか?(^^;;
ぜひお願いしたいです。
お役に立てて幸いです。
出版については、以前ある出版社からの依頼が苦い経験だったため、選択肢から消していました…。
でも、需要があるのならまた検討してみます(kindleとか)。
いずれにしてもうれしいお言葉ありがとうございます。
すいません質問なんですけど
問1)子どもが8時に、家から体育館へ向けて走りはじめた。20分後に、子どもの忘れものに気づいた母が自転車で追いかけた。子どもの速さを分速120m、母の速さを分速270mとすると、母は何時何分に子どもに追いつくか。
この問題は、
270x=120(20+x)
150x=240
X=5分の8
になりますよね
で5分の8は96分になるから1時間36分で、子供が8時に出たから母が子供に追い付く時間は9時36分になるんじゃないんですか?
答えは8時36分になってますけど
再コメントありがとうございます。
問1は
270x=120(20+x)
270x=2400+120x
150x=2400
x=16
となり、8時の20分後からさらに16分後なので、8時36分です。