前回につづき、中1数学「文字と式」の具体的な教え方について解説します。
今回はかっこ外しと分配法則です。
ただその前に、ひとつ注意すべき点があります。
それは文字式の計算単元に入った段階で、
- 途中式を書く習慣がない生徒
- 分数計算ができない生徒
は必ずつまずくという点です。
というか、文字式単元でつまずく生徒というのは、必ずといっていいほど、途中式を正しく書けない、あるいは分数計算ができない子なのです。

だから文字式単元に深く分け入っていく前に、この2点ができているか確認しなければいけません。
そしてできていなければ、すぐに解消してやらねばなりません。
そうでないと、今後の数学の授業に一歩もついていけないことになります。
「1学期中間テストは良かったのに、期末テストで急に点数が落ちた…」。
「小学校ではよくできるほうだったのに、中1の夏あたりから落ちこぼれた…」。
よくあるパターンですが、こうなってしまいかねません。
そこでまず今回は、途中式と分数計算の指導について解説します。
そのあと、かっこ外しと分配法則という該当単元の内容を見ていきます。
[前の記事]文字と式①:文字式計算の導入
[次の記事]文字と式③:分数まじりの複雑な計算
(数学指導法の記事一覧はまとめページへ)
スポンサーリンク
途中式が書けない・分数計算ができない

途中式を正しく書かない子。
分数計算、とくに異分母のたし算・ひき算ができない子。
これらの中学生は「文字と式」単元から徐々に数学が嫌いになっていきます。
なぜなら、「文字と式」単元の計算問題以降、途中式を正しく書けること、分数計算ができることは当たり前とみなされるからです。
上図のような問題でも、先生はもう「4と6の最小公倍数を考えて…」なんていちいち解説しないからです。
ここで「え?なんで分母が12や8になるの?」と戸惑うか、戸惑わないか。
これが中1数学最初のおおきなターニングポイント。
もし戸惑うなら、以下の指導例を参考にして、すぐに解消してあげてください。
![]()
原因
途中式が正しく書けない、書こうとしない。
異分母の分数計算で悩んだり、手が止まる。
これらの症状はともに、小学5年生の「分数のたし算・ひき算」に原因があります。
具体的には、
- 途中式を正しく書く手順が身についていない
- 最小公倍数をパッと導く訓練が足りていない
この2つが主な原因です。
\begin{eqnarray} \frac{3}{4} + \frac{1}{6} &=& \frac{9}{12} + \frac{2}{12} \\&=& \frac{11}{12} \end{eqnarray}
よって、このような小5の問題が「速く」「正確に」できるようになるまで、練習する必要があります。
小学5年生の算数ドリルなどを用意して、以下の順番で指導しましょう。
なお、親御さんがわが子にさせる場合、ネット上に無料問題もあります。
十分な問題数が必要ですが、検索したらこんなサイトも見つかりました↓
PDF算数・計算ドリルの算願 –算数と計算ドリルの無料ダウンロード–
*塾や家庭教師などでの2次使用には許可が必要です。詳しくは各サイト先のプライバシーポリシー等をご確認ください。
![]()
指導案
①約分の練習問題をさせる。
最初は目の前でさせてみて、最大公約数で約分することを徹底する。
瞬時にできるようになるまで、10問でも、1000問でも、させる。
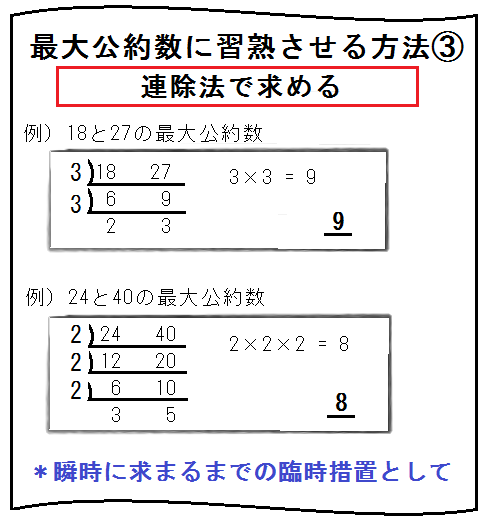
*最大公約数に習熟する方法は「注意点」を参照。
②通分の練習問題をさせる。
最初は目の前でさせてみて、最小公倍数で通分することを徹底する。
瞬時にできるようになるまで、10問でも、1000問でも、させる。
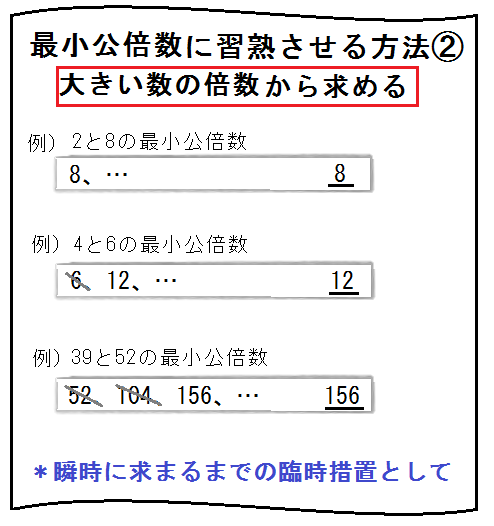
*最小公倍数に習熟する方法も「注意点」を参照。
③約分の逆を練習させる。
やはり最初は目の前でさせて、説明はせず、生徒ができたらただ誉めればいい。
瞬時にできるようになるまで、10問でも、1000問でも。
④以下のような異分母のたし算問題を示し、生徒と一緒に解きすすめる。
先生「分母がちがう。だからまず、分母をそろえる」
先生「□に入るのはいくつ?」
生徒「2」
→2と書き入れる。
先生「あとは分子を計算する。いくつ?」
生徒「3」
→答えを書く。
先生「8分の3は、約分できる?」
生徒「できない」
先生「じゃこれでおわり」
⑤おなじ問題を再び書き、今度は生徒にやらせる。
このとき必ず途中式を書くことを徹底する。
その後、類似問題をいくつか目の前でさせる。
慣れてきたら自分ひとりで練習させる。やはり10問でも、1000問でも。
⑥異分母のひき算を、たし算と同様の手順で。
注意点
最大公約数を求めるのにどうしても時間のかかる生徒がいます。
そんな子には、正負の数:乗除の記事でも書きましたが、以下3通りの方法のうちどれかを試してみてください。
また、最小公倍数をパッと出せない場合も、以下3方法のどれかを試すといいでしょう。
そして、もうひとつ大事な注意点があります。
それは、こうした復習のスケジュールを生徒と共有すること。
どれくらいの期間、復習をしたら、中学の内容に戻るのか、はっきり伝えてからはじめましょう。
個人的には、宿題や夏休みを最大限利用して、遅くとも2か月以内がベターと思います。
それ以上かかると、生徒のヤル気がもちません。
「2か月後には計算バリバリになる!」等と言って、がんばらせてください。
そして一刻もはやく「途中式が正しく書ける」「分数計算もへっちゃら」「だから文字式の計算だってスラスラできる」状態を味わわせてあげてください。
かっこ外しでまちがえる
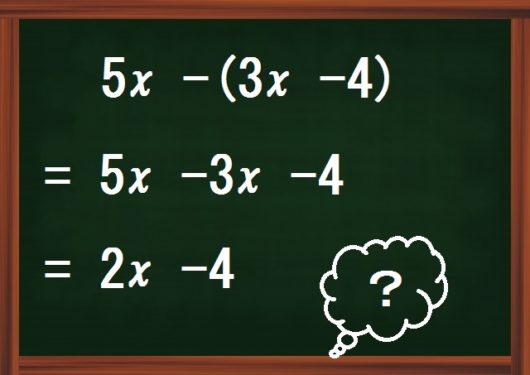
さて、途中式が正しく書け、分数の加減もパッとできるようになったら、いよいよ文字式計算に深く分け入っていきます。
具体的には、かっこ外しと分配法則です。
ただ、かっこ外しの場合、対処はそんなに難しくありません。
前回の記事でも書いたように、ルールを徹底させていくだけです。
原因
かっこ外しのルールが身についていない
かっこ外しの計算でつまずく原因は、これです。
だから、ルールをしっかりと言って聞かせ、実際にやってみせ、目の前でさせて、たくさん練習させるという順番を守って指導すれば、おのずと身についていきます。
ただ、これ以外の原因でつまずく生徒というのも実際います。
つまり、以下3つの原因でつまずくパターンです。
- かっこを外したあとの計算でつまずく
- 途中式を書かずにやろうとしてまちがえる
- 分数の加減になると途端に手がとまる
1.に関しては、まず文字式最初の計算を習熟させることが必要です。
前回の記事を参照して、じゅうぶんに習熟させてください↓。

2.と3.に関しては、上で書いたとおりです。
指導案
① \( 5x + ( 3x – 4 ) \)
例題を示し、かっこの中が計算できないことを確認する。
このような式は、かっこを外してから計算すると伝える。
そして、かっこ外しのルールを伝える。
②例題を、発問しながら解きすすめる。
先生「かっこの中に項は2つある。何と何?」
生徒「 \(3x\) と \(-4\) 」
先生「 \(3x\) の符号はどっち?」
生徒「プラス」
→以下のように+と書く。
先生「かっこの前は+、-どっち?」
生徒「プラス」
先生「じゃ、符号はそのままで外す」
→以下のように書く。
まだ計算できることを確認して、計算させる。
そして答えを書く。
③かっこの前が-の場合も、同様にしてすすめる。
このとき、うしろの項も「ぜんぶ符号を逆にする」と強調する。
④類似問題を目の前で解かせる。
よくできたら誉め、まちがえたら訂正する。
なお、いちばん前にかっこのある式は、前に「+」が隠れている、だからそのまま外すと伝える。
例:\( (2x-3y) – (4x +5y) \)
⑤あるていど計算に習熟した段階で、「じつは分配法則だ」と伝える。
図のように、1と×が省略されている。
本当は分配法則だから、うしろの項にもかけることを忘れるな、と念を押す。
⑥練習問題をさせる。
注意点
⑤番目に「じつは分配法則だ」と伝えることで、うしろの符号をまちがえるというミスが少なくなります。
また次の、かっこの前に数字のある計算にもスムーズに移行できます。
しっかりと伝えてあげてください。
なお、ここで「分配法則だ」と伝えてストンと腑に落ちるには、それ以前に、かっこ外しとはじつは乗法であると感じていることが重要です。
よって、正負の数:かっこ外しでは「同符号なら+、異符号なら-」等と教えないこと。
また、正負の数:四則混合では「+-の前で式を区切る」とアドバイスすること。
先々をみすえた指導、計算の本質に沿った指導を心がけましょう。
分配法則でまちがえる
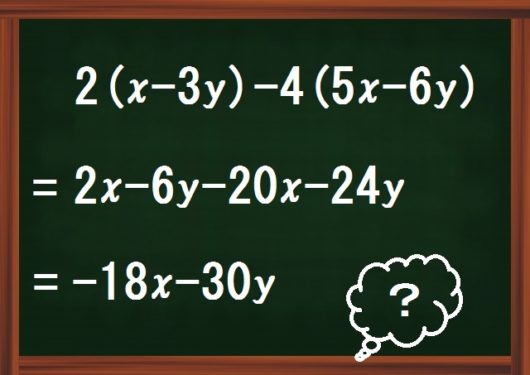
最後に、分配法則の基本問題でつまずく場合について解説します。
ここでも、ミスをする生徒は多くみかけます。
とくに上図のように、かっこの後ろの符号や数字をまちがえるパターンが圧倒的。
原因を把握して、解決していきましょう。
原因
文字式の分配法則でつまずく原因は、次の3つです。
- 文字式の乗法が身についていない
- 項のかたまりを捉えられていない
- 単純に、練習不足
1.について。
学校ではかっこ外しのあと、(1次式)×(数)の乗法を習います。
\(5x \times (-4) \) や \(-6a \times \left( -\frac{3}{4} \right ) \) などです。
この文字式の乗法がしっかり身についていないと、分配法則でもつまずくことになります。
2.について。
たとえば \(-4( 5x-6y) \) のうしろを \(-24y\) とする生徒は、\(-4\) という項をかたまりとして捉えていない可能性があります。
つまり、ひき算マークのあとに \(4\) がついていると、誤解しているのです。
これは「正負の数・加減」記事内で述べたように、+-を符号と徹底していれば防げるミスです。

しかし学校では、+-が符号なのか計算記号なのかあやふやなまま文字式に入るので、こうしたミスが生まれます。
再度、ここで、+-とは数字の前についた符号だと意識づけする必要があります。
![]()
3.については、そのまんまです。
「わかる」と「できる」は違います。
生徒が「できる」ようになるまで、何十問でも練習させましょう。
指導案
①以下のような例題を示し、(1次式)×(数)をおさらいする。
$$ 5x \times (-4) $$
このとき、符号→数字→文字の順で計算することを徹底する。
「符号は?」「マイナス」
「数字は?」「\(20\)」
「文字つけて」「\(x\)」
→ \(-20x\) と。
②類題をいくつか目の前で解かせたのち、(1次式)×(数)の練習問題をさせる。
ここでも、符号→文字→文字の順で計算することを徹底する。
③ \(2(x-3y) \) のような例題を示す。
そして「×が省略されている。だから、分配法則でかっこを外す」と伝える。
図のように印をして、分配の計算をさせていく。
「\(2 \times x \) 。符号は?」「プラス」
「数字は?」「\(2\)」
「文字は?」「\(x\)」
「そう、つまり?」「\(2x\)」
「\(2 \times (-3y) \) 。符号は?」「マイナス」
「数字」「\(6\)」
「文字」「\(y\)」
「つまり?」「\(-6y\)」
④ \(-4(5x-6y) \) のような例題を示し、同様にしてすすめる。
×マークはもう書かないこと。
他の印はすべて書くこと。
そして符号→数字→文字の順番で計算させること。
⑤類題をいくつか目の前で解かせたのち、練習問題をさせる。
⑥以下のような例題を示し、同様の手順ですすめる。
2つめの式が出たら、「まだ計算できる?」と聞いて、最後まで計算させる。
⑦類題をいくつか目の前で解かせたのち、練習問題をさせる。
注意点
文字式の乗法はつねに「符号」→「数字」→「文字」の順番で計算すること。
これが生徒の頭に定着するまでは、指導案のように、こまかく質問するといいでしょう。
もうミスはないなと判断した段階で、一発で計算するように切り替えます。
切り替えのタイミングは、目の前で数問解かせているときがいいと思います。
また、はじめのうちは生徒自身に〇や→や下線などの印を式に書きこませてもいいでしょう。
とくに、自分のやり方にみょうな自信をもっている子。
また、言語能力は低いけど視覚情報にはするどく反応する子。
そんな子には、印を書かせる指導はとりわけ有効です。
ちなみに前者は、計算だけ速い子に多いです。
後者は、ゲームが得意な子に多い印象です。
なお、以下のような問題も分配法則をつかった計算です。
$$ \frac{2}{5} (10x-25) \quad \frac{4x+5}{3} \times 6 $$
$$ (9x-6) \div (-15) \quad \left( -\frac{1}{3}x – \frac{3}{4} \right) \div \frac{5}{12} $$
$$ \frac{3x-y}{4} – \frac{5x-7y}{6} $$
これらの指導については、次の記事でまとめて解説します。
![]()
まとめ

○途中式を書かない・分数計算ができない生徒に…
文字式の計算に深く分け入っていくまえに、小5「異分母のたし算・ひき算」を復習する。
「約分」→「通分」→「約分の逆」→「異分母のたし算」→「異分母のひき算」の順番で練習する。瞬時にできるようになるまで、何百問でも。
最大公約数・最小公倍数を求めるのに時間がかかる場合、上で紹介した方法のどれかを試させる。そして、2か月以内などと期間を共有して復習させること。
○かっこ外しでまちがえる生徒に…
かっこ外しのルールが身についていないのが原因。きちんと伝えて、たくさん練習させる。
具体的にはまず、「かっこの前が+:符号そのまま」「かっこの前が-:符号ぜんぶ逆」とルールを伝える。次に項それぞれの符号を意識させながら、やってみせる。あるていど練習させたのち、じつは分配法則であるとバラす。そしてまたたくさん練習させる。
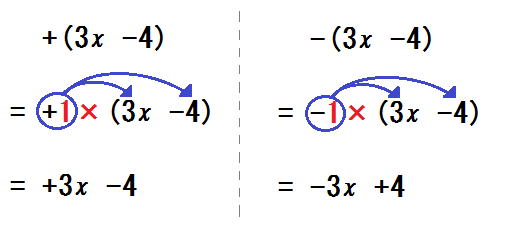
○分配法則でまちがえる生徒に…
「文字式の乗法が身についてない」「項をかたまりとして捉えられてない」「練習不足」の3つが原因。
そこで(1次式)×(数)をまず復習する。次に、ビジュアルに訴えることで項のかたまりを意識させながら、分配計算をやってみせる。そして類題を目の前でさせたのち、たくさん練習させる。
ポイントは「符号」→「数字」→「文字」の順でつねに乗法すること。また、項のかたまりを印で自然と意識させること。
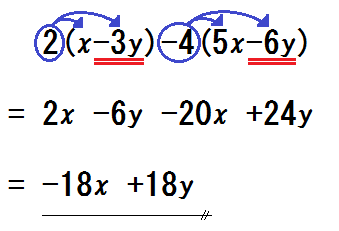
この記事は管理人のジュウゴが、過去の経験といろんな書籍情報をもとに書いています。
今後のさらなる経験や情報によって、改訂されていく余地アリです。
よって教育に携わる方からのご意見・ご感想は大歓迎です。
下のコメント欄から、随時おまちしています。

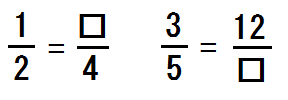
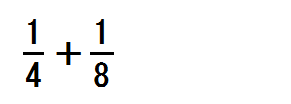
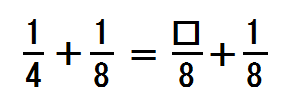
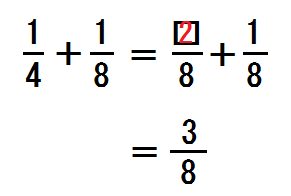








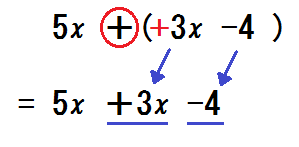

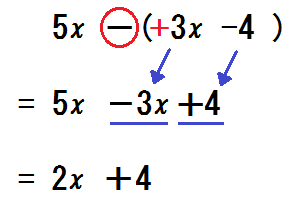


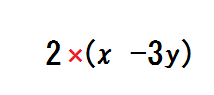
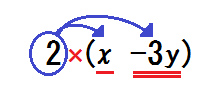
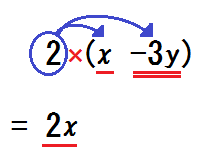
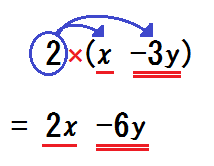



コメント
途中式を書けない、書こうとしない生徒は多いので、
とても興味深く拝見しました。
途中式を書く習慣をつけるためには、
「分数の足し算、引き算」の演習をするのがよい、
ということでしょうか?
それはなぜでしょうか?
例えば、5×(4-1)のような四則演算で途中式を書かせることも考えられますが、
それよりも「分数の足し算、引き算」の方が効果的なのでしょうか?
5×(4-1)を暗算できる小・中学生はいますが、
異分母の足し算・引き算をすべて暗算できる子はほとんどいないからです。
そこで、すぐに答えが出なくて手が止まっている場合の解決策として、途中式を導入する。
するとスムーズに子どもは受け入れてくれます。
これが小5の「異分母の足し算・引き算」で途中式を導入・定着させる理由です。
回答ありがとうございます。
なるほど。
そういう意味では、中学生ともなると、
上に例示されている、(3/4)+(1/6)程度の計算は、
暗算でできる生徒も少なくありません。
暗算ではできない程度の問題も含めて定着させるのがよさそうですね。