中学数学の教え方について、具体的に解説するこの連載。
今回から中学1年生の2単元目「文字と式」になります。
文字式になって数学がわからなくなった…
文字式の計算で、利用でつまずいている…
そんな生徒への指導に、ご参考ください。
[前の記事]正負の数③:四則混合、分配法則
[次の記事]文字と式②:途中式と分数、かっこ等
(数学指導法の記事一覧はまとめページへ)
1回目はまず「文字式の計算」の最初です。
とくに以下のようなまちがいをする生徒、
\begin{eqnarray} & & x-3-2 \\&=& -5x \end{eqnarray}
\begin{eqnarray} & & 4m-(2-3m) \\&=& 4m-2-3m \\&=& m-2 \end{eqnarray}
\begin{eqnarray} & & 2(a-3b)-4(5a-6b) \\&=& 2a-6b-20a-6b \\&=& -18a-12b \end{eqnarray}
つまり文字式の最初の計算が正しくできない。
また、かっこ外しでまちがえてしまう。
そして、分配法則でもつまずいている。
これら3点について、原因・解決法・注意点をそれぞれ解説していきます。
なお、いちばん初めに習う「文字式の表し方」については省略します。
「正負の数」記事で指摘したとおりの指導をしていれば、そして表し方のルールをすべて暗記させれば、ここでつまずくことはまずないからです。
もし \( x \div y \times z = \frac{xz}{y} \) ができない場合は正負の数:乗除の記事を。
\( a \times (-3) -4 \div b \times c =-3a-\frac{4c}{b} \) ができない場合は正負の数:四則混合の記事を、それぞれ参照してください。
スポンサーリンク
最初の計算でつまずく
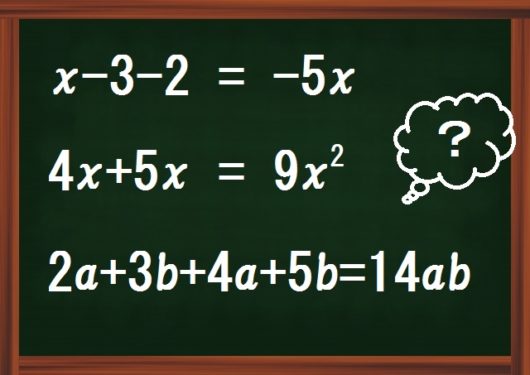
文字式の計算単元になると、上図のようなまちがいをする生徒が急に現れます。
こんなまちがいをするとは…。
われわれ大人は戸惑いつつも愕然とし、なんとか理解させようと説明につとめます。
「文字ってのは小学校で習った□や○とおなじなんだ」
「かけ算と+-はちがうだろう」
「6匹のネコと8人の人間、一緒にしちゃダメ」等々。
しかしこんな説明をされればされるほど、子どもの顔は曇っていきます。
文字式の最初の計算を習熟するために必要なこと。
それは、わかりやすい説明ではないのです。
原因
文字式の最初の計算でつまずく主な原因は、たったひとつです。
文字式の計算のルールが身についていない
これだけです。
そしてルールが身につかない理由は、理解していないから、ではありません。
正しいルールでおこなう練習の量が足りていないのが理由です。
いま、文字式の最初の計算でつまずいているわが子、または担当の生徒を思いかえしてください。
家庭学習の習慣はありますか?
宿題は毎回きっちりやっていますか?
おそらく大半の生徒ができていないはずです。
そこで、文字式の最初の計算を習熟させるためには、子どもがすすんで練習するような働きかけ、つまりアメとムチが必要になります。
[文字と式の記事一覧]
- 文字と式①:文字式計算の導入
- 文字と式②:途中式と分数、かっこ外し、分配法則
- 文字と式③:分数まじりの複雑な計算
- 文字と式④:数量の表し方
- 文字と式⑤:規則性の問題
指導案
①以下のような計算を示し、やってみせる。
\begin{eqnarray} & &4a+2a = 6a \\& & 3b+5b = 8b \end{eqnarray}
「このように、文字がおなじもの、つまり仲間同士は計算できる」と伝える。
②以下のような例題を示し、発問していく。
教師「4aの仲間はどれ?」
生徒「2a」
教師「符号までふくめて言って」
生徒「+2a」
教師「そのとおり」
下のように下線を引く。
教師「4aと+2a、計算するといくつ?」
生徒「6a」
教師「よくできた」
次の式に計算結果を書く。
教師「次、+3bの仲間はどれ?」
生徒「5b」
教師「符号までふくめて言ってな」
生徒「あ、+5b」
教師「すばらしい」
下のように波線を引く。
教師「+3bと+5b、計算して」
生徒「8b」
教師「符号はどっち?」
生徒「プラス」
次の式に計算結果を書く。
教師「\( 6a+8b \) 、まだ仲間同士ってある?」
生徒「ない」
教師「じゃもう計算できない。だからこれで終わり」
③つづけて以下のような例題を示し、同じ手順で発問しながら解きすすめる。
\begin{eqnarray} & & 4x+3y-5x-6y \\& & 2n-7-n \\& & x-3-2 \\& & 2x^2 -4x +3x^2 -5x \\& & x^2 -6x -3 +2x^2 +4x +5 \end{eqnarray}
このとき、生徒が正解すれば適宜ほめてやる。
生徒がまちがえたら、説明はせず、即座に正しい答えを言う。
④同様の練習問題を目の前で解かせる。
生徒が計算に慣れてきたら、自分ひとりでさせる。
ここでも、正答は適宜ほめること。
まちがえたら、ただ正しい答えを伝えること。
⑤同様の練習問題を宿題に出す。
「必ずやってこい!来週チェックする」などと言って脅す。
そしてやってきたらオーバーすぎるくらいに誉めてあげる。
注意点
以上の指導案はあくまで一例ですが、アメとムチの使い分けがわかると思います。
このように、こちらが望む結果を生徒が出したときにはアメを。
ルールを伝えるとき、まちがえたとき、そして宿題を出すときにはムチを。
生徒の個性に応じて、それぞれ差し出したり、チラつかせたりしましょう。
この点で、文字式最初の計算でつまずいた生徒への指導には、論理的に説明する技術よりも、生徒をノせる技術が必要であるといえます。
とくに、気の優しい人はムチを使うのが苦手です。
生徒の前に出たら役者だと思って、ときには厳しい先生を演じてください。
また、この指導案では「同類項をまとめて」とは言わず、「仲間同士を計算」と言っています。
なぜ同類項という数学用語を使わないのか?
理由は2つあります。
ひとつ。\( x-3-2 \) において \(-3\) と \(-2\) は厳密には同類項じゃないから。
つまり同類項とは、文字をふくんでいる項のうち、その文字がまったく同じである項を言うのです。
「便宜上であってもまちがったことは教えない」というのが私の姿勢です。
ふたつ。いたずらに数学用語を使うと生徒の頭に?が増えるから。
つまり、文字式最初の計算でつまずく生徒というのは、学力下位の子が多い。
そんな生徒にいたずらに数学用語を使うと混乱をまねくだけだと考えるからです。
以上2つの理由から、私は「同類項をまとめて」とは言っていません。
なぜこの教え方か?
「この教え方では、理由なしにただルールを押し付けているだけじゃないか。つめこみ教育だ。これでは生徒の考える力を伸ばせない」。
こんな反論をもつ方もおられるでしょう。
しかし私は、つめこみ教育は必要と考えます。
ここでちょっと、ジュウゴの失敗談を聞いてください。
大学生の頃、私もつめこみ教育に反対していました。
「もっと生徒に考えさせて。もっと主体的な学習を」。
そんな理想に燃えて、塾講師や家庭教師のアルバイトをはじめました。
が、出会う生徒の大半は勉強に落ちこぼれて、ヤル気を失っている子ばかり。
なぜ文字を使うのか、なぜ \(6a+8b\) はこれ以上計算できないのか。
手をかえ品をかえ必死に説明しても、数学の魅力なんてこれっぽっちも感じてくれません。
結局、お菓子で釣ったりして、どうにか頑張らせていただけでした。
卒業後、教育関係の仕事に就いた私は、180°態度を変えました。
大学時代の反省から、生徒には厳しく当たろうとしたのです。
「とにかく覚えろ。反論はゆるさん」。
生徒たちは緊張感をもって、黙々と勉強していきました。
結果、学力向上する子も多く、生徒の数も日増しに増えていきました。
しかしいっぽうで、常に有無をいわせない私の態度に反発した子が退塾するようにもなりました。
不器用な私には、アメとムチの使い分けや、子どもの性格によって柔軟に対応することができなかったのです。
以上が20代半ばまでの私の失敗です。
それからはたくさんの書籍を読み、多くの先輩指導者に学び、勉強しなおしました。
とくに北欧や東アジアの教育制度から、「考える力」や「主体性」にはまず一定量の知識・練習の蓄積が前提として必要であると学びました。シンガポールや中国はいわずもがな、フィンランドでさえ留年と卒業延期制度で練習量を確保していたからです。
また、生徒のモチベーションを保つには、その子その子の性格を見ぬいたうえで適切な声かけが必要であると教えられました。一概に優しく、一概に厳しくではダメだと。子どもによって、その日の状態によって、アメとムチを使い分けると。だからこそ生徒をよく観察することが大事だと学びました。
このような経験と学びから、私は上記の指導案をおすすめするんです。
つまり、まず理由なしに文字式の計算ルールを伝える。
習熟させる際には、生徒をよく観察して、アメとムチを使い分ける。
「文字を用いることの必要性と意味」(中学校学習指導要領)を教えるのはそのあと。
こういう順番です。
そもそも、数学を習う意味を本当に理解するのは大人になってからですね。
文字式に習熟し、方程式の解法を身につけ、関数を知り、高校数学を習い、線形代数で経済を分析し、解析学を応用して建物を設計する。そうなってはじめて、私たちは「文字を用いることの必要性と意味」を真に理解します。
この意味で、数学教育とは「わからなくていいから、まずできるようになれ」。
よって指導者に求められるのは、意味はわからないけどとにかくできるようにする、そのための生徒のモチベーションづけです。
アメとムチを使い分けて、文字式の計算がまずはちゃんとできるようにしてあげましょう。
「実は文字を使うわけってね…」なんて話は、そのあとにしましょう。
とりあえずのまとめ

思いのほか記事が長くなったので、ひとまず区切ります。
○文字式の計算の最初でつまずく生徒に…
つまづきの原因は、理解していないからでなく、計算ルールを身につけるための練習量が足りていないこと。
練習量を確保できるように、生徒のモチベーションを高めながら指導する。具体的には、項を意識させながらやってみせ、次にさせてみて、よくできたら誉め、ミスしたらただ訂正すること。そして宿題をきちんとやるようにハッパをかけること。
なぜ文字を使うのか、なぜ \(6a+8b\) はこれ以上まとめられないのか。そんな話は計算に習熟したあとでいい。
NEXT→中学数学「文字と式」でつまずく原因と解決法② 途中式と分数、かっこ外し、分配法則
長くなったついでに、ひとつ余談を。
さきほど、数学教育とは「わからなくていいから、まずできるようになれ」というものだと書きました。
やがて大学や仕事で数学を使うようになってはじめて、必要性や意味を実感できるのだと。
しかしこう言うと、以下のように指摘する人もいます。
「わたし、大人になっても数学使ってないし」。
「おれ、数学使うような仕事には就かねぇし」。
これに対する私の答えは、英語について書いた以下の記事の内容とまったく同じです↓。

つまり、大人になっても数学を使う人は全体の1割程度ですが、その1割の人間が現代社会のあらゆるテクノロジーを維持・発展させてくれるおかげで、わたしたちは原始人並みの生活をしなくてすむんです。
その1割を生み出すためには、全体に網をかけて義務教育段階から数学を教えるしかありません。
だから数学教育は必要なんです。
いま目の前にいる生徒が、中学生のわが子が、将来エンジニアやプログラマーになるかもしれないですもんね。
数学教育にかんするこうした私の考えは、じつは東野圭吾の著作を読んで固まりました。
『容疑者xの献身』で、石神という数学教師は生徒に以下のように語ります。
「森岡はバイクが好きだそうだな。オートレースを見たことあるか」
唐突な質問に、森岡は戸惑った顔で頷いた。
「レーサーたちは一定速度でバイクを走らせるわけじゃない。地形や風向きに応じてだけでなく、戦略的な事情から、たえず速度を変えている。どこで我慢し、どこでどう加速するか、一瞬の判断が勝負を分ける。わかるか」
「わかるけど、それが数学と何の関係があるわけ?」
「この、加速する度合いというのが、その時点での速度の微分だ。さらにいえば、走行距離というのは、刻々と変化する速度を積分したものだ。レースの場合は当然、どのバイクも同じ距離を走るわけだから、勝つには速度の微分をどうするか、というのが重要な要素になってくる。どうだ、これでも微分積分は何の役にも立たないか」
石神の話した内容が理解できないのか、森岡は困惑した表情を浮かべた。
「だけどさ、レーサーはそんなこと考えてないぜ。微分とか積分とかなんて。経験と勘で勝負してるんだと思うな」
「もちろん彼等はそうだろう。だけどレーサーをバックアップしているスタッフはそうじゃない。どこでどう加速すれば勝てるか、綿密にシミュレーションを繰り返し、戦略を練り上げる。その時に微分積分を使う。本人たちに使っている意識はないかもしれないが、それを応用したコンピュータソフトを使っているのは事実だ」
「だったら、そのソフトを作る人間だけが数学を勉強すりゃいいじゃねえか」
「そうかもしれないが、森岡がそういう人間にならないともかぎらないだろ」
東野圭吾『容疑者xの献身』文春文庫、p154-155
作家の東野圭吾は理系出身で、デンソーの技術者だったそうです。
以下のエッセーでは、数学教育の意義についてより直接的に書いてます。
「数学は何のため?」という箇所です、おススメですよ。
長くなりすぎたので、余談はここまで。
次回は文字式の計算において、途中式を正しく書けない、分数になるとできない場合の解決法。
そして「かっこ外し」と「分配法則」でつまずく場合の解決法について、解説していきます。




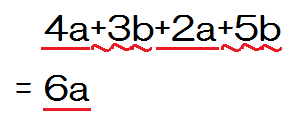












コメント
意味がわかりました!
体験談、興味深く拝見しました。
>そしてルールが身につかない理由は、理解していないから、ではありません。
>正しいルールでおこなう練習の量が足りていないのが理由です。
その通りだと思います。
>いま、文字式の最初の計算でつまずいているわが子、または担当の生徒を思いかえしてください。
>家庭学習の習慣はありますか?
>宿題は毎回きっちりやっていますか?
>おそらく大半の生徒ができていないはずです。
はい、大半の生徒ができていません。
自分なりにアメとムチを使い分けているつもりですが、
宿題をやってこない生徒は、何年たっても、宿題をやってくるようにはなりません。
そのため、何年たっても、成績が伸びないのが現実です。
宿題をやってこさせるためにはどうしたらよいか、アドバイスを頂けたら幸いです。
>宿題をやってこさせるためにはどうしたらよいか、アドバイスを頂けたら幸いです。
宿題の定着は難しいですよね。
私もよくて8割というところです。
まず通塾して何年も経つ生徒は、本人の意識改革がないかぎり、ムリです。
よってこれからの新入生に対して「宿題はやって当たり前」という態度で臨む。
そういう新入生が半数以上を占めるようになって初めて、塾全体の雰囲気が変わります。
あとは日々、宿題をする利点を伝えつづけること、宿題をやってきた生徒は周りに聞こえるようにほめること、保護者面談ごとに家庭学習の定着のコツを伝えること、そして「この子はできるようになる」と信じつづけること、などをジュウゴは実践しています。
以下の記事もご参考ください。
小学生のうちに学習習慣を!家庭内で決めるべき5つのルール
アドバイスありがとうございました。
特に、最後の、
>「この子はできるようになる」と信じつづけること
には、目が覚める思いです。
めげずに信じ続けたいと思います。
とてもわかりやすい
アドバイスをいただき
ありがとうございます!
これからも活用していきたいです!
教えてください。
中1の数学で、c/abを×や÷を使って表せという問題で、c÷(a×b)と答えて
バツになりました。間違いの理由を教えてください。(/は分数です)
ちなみに正解はc÷b÷aでした。
c÷(a×b)
c÷a÷b
計算上はどちらも正解です。
ただ数学では「省略できるところは省略して、できるだけ短く表記する」という習慣というか伝統があります。
よって、上の表記はかっこが余計なので、あまり使いません。下の表記のほうが一般的です。
バツになったのは、計算の間違いではなく、数学の習慣に反しているからでしょう。
今後、高校入試などでも「できるだけ短く表記」していない回答はバツになるので、「計算はまちがってないけど、まあ習慣に従っておこうか」ぐらいに思っておけばいいでしょう。