中学数学「正の数・負の数」解説の3回目。
勉強のしかたではなく、どのように教えたらいちばん理解が早いのかという具体的な教え方を書いていきます。
正負の数でつまずいている生徒。
わからない・できないという生徒。
定期テストでぼろぼろだった生徒。
そんな子への指導案としてご参考ください。
[前の記事]正負の数②:乗除、累乗
[次の記事]文字と式①:文字式の導入
(数学指導法の記事一覧はまとめページへ)
今回は四則混合と分配法則について。
とくに四則混合はつまずく生徒の多い箇所です。
が、おおきく戻って復習する必要はありません。
ここで紹介する方法を使えば、ほとんどの生徒が難なく習熟していきます。
以下、つまづきの原因・解決策・注意点を見ていきましょう。
スポンサーリンク
四則混合でつまずく
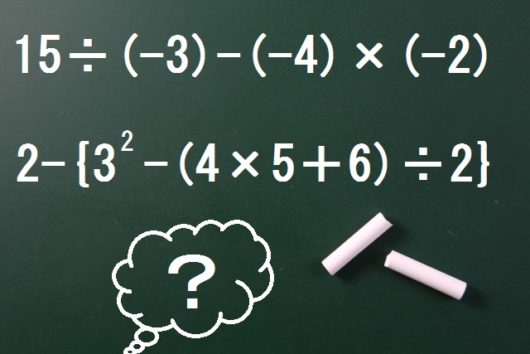
「正負の数」における四則混合計算とは、いままでのいろんな計算の総動員です。
だからここでつまずく生徒には、時間をかけて、小学校の算数からすべてやり直させる。
そんな指導をしていた時期もありました。
しかしあるとき先輩指導者から、もっと効率的で時間のかからない方法を教わったのです。
ポイントは2つ。
計算の順序を徹底すること。
そして式を+-の前で区切ることです。
原因
「正負の数」の四則混合でつまずく原因は、とくに以下の3つです。
- 計算の順序が身についていない
- 途中式を書く習慣がない
- 「+」「-」が符号なのか計算記号なのかあやふや
1.に関しては小4の「四則計算」。
2.に関しては小5の「異分母の分数のたし算・ひき算」。
3.に関しては1回目の記事で述べたように、中1最初の「正負の数の加減」。
つまづき箇所に応じてそれぞれの単元を復習する、というのもひとつの手ではあります。
しかし、復習せずとも、これらのつまづきを解消することもできます。
指導案1
①生徒のノート、またはテキストの余白などに、以下の文を書かせる。
「これから×÷や+-や括弧とかの混じった計算をする。ぜんぶ、この順序でする」と伝える。
②例題を出し、×÷と+-が混じっていることを確認させる。
それからこう伝える。
「どんなふうに解けばいいか?+-の前で式を区切ればいい」。
そして実際に式を区切ってみせる。
このとき、「かっこの外にある+-の前で区切る」と注釈する。
③区切りそれぞれを計算すると伝え、質問しながら生徒に答えさせる。
\( 15 \div (-3) \) において、
「-は何個ある?」「1コ」
「じゃ符号はどっち?」「-」
「数字は?」「5」
\( -(-4) \times (-2) \) において、
「-は何個ある?」「3コ」
「じゃ符号は?」「-」
「数字」「8」
このように生徒が答えるたび、途中式を書きこんでいく。
④「×÷が無くなったね、あと、これ計算して」と言って、答えさせる。
⑤もう1、2問くらい例題を示したのち、同様の練習問題を一緒に解く。
生徒が計算に慣れてきたら、自分でさせる。
指導案2
①つづいて、かっこの中に計算のある例題を出す。
冒頭に書かせた≪計算の順序≫を見せながら、「かっこの中に計算があったら、まずかっこの中からする」、「かっこがたくさんあったら、いちばん中にあるかっこからする」と伝える。
「つまり、ここから」と言って、最初に計算する部分を囲む。
②かっこの中に×と+が混じっているので、式を区切る。
区切りだけ計算したものを、次の式に書く。
このとき、計算していないものはそのまま変わらず書くことと強調する。
③「次はどこを計算する?」と聞く。
生徒が答えられなければ≪計算の順序≫を見せ、さらに「かっこがたくさんあったら、いちばん中にあるかっこからする」とヒントを出す。
正しく答えた段階で、またその部分を囲む。
囲み内に累乗や×÷がないことを確認してから、計算させ、次の式を書く。
④「次はどこを計算する?」「このかっこの中」
「かっこ内に、累乗や×÷はある?」「ある」
「じゃ式を区切ろう」と言って、式を区切る。
そして区切りそれぞれを答えさせる。
⑤「次はどこを計算する?」「ここ」
「かっこ内に累乗や×÷はある?」「ない」
「じゃ計算して」。させる。
⑥「まだかっこ内の計算、ある?」「ない」
「じゃ、あとは≪計算の順序≫の②と③だけだ。累乗や×÷はある?」「ない」
「+-だけだな。このかっこ外そう、符号はどっち?」「+」
次の式を書く。
「最後、計算して」「6」
最後の答えを書く。
⑦このように、常にかっこの中から計算すること、そして累乗や×÷があったら式を区切ること。
そうすればどんな複雑な四則混合でも正解にたどりつける、と伝える。
同様の練習問題を一緒に解き、生徒が計算に慣れてきたら、自分でさせる。
注意点
累乗と×÷の同時計算がむずかしい場合は、「累乗」→「×÷」の順でさせましょう。
つまり、下の例のように途中式を一手、追加させます。
また、かっこの中を計算したら計算結果がマイナスだった場合、かっこは付けたままにさせることにも注意です。
つまり、下の例のようにです。
他にも、途中式を正しく書けているか、注意することが必要です。
ただ、これら3点をいちいち説明するのはめんどくさい。
生徒も注意点がいっぱいあって、頭がこんがらがります。
だからこそ「一緒に解く」、つまり目の前でさせてみるという過程が大事なのです。
目の前で解かせながら、適宜声かけをしてやればいい。
「途中式、ひとつ増やしていいぞ。こんなふうに」とか。
「--1っておかしいよな、この場合はかっこ付けたまま」とか。
「ここ、なんかヘンだよ」とか。
重要なポイントは、あらかじめ言って聞かせる。
細かい注意点は、させてみて、そのつど伝える。
生徒を導く際には、常にこの使い分けを意識するといいでしょう。
あの山本五十六も言ってますもんね。
なぜこの教え方か?
「(かっこの外にある)+-の前で式を区切る」。
ここで紹介した指導例のいちばんのポイントは、これです。
しかし、1回目の記事でも触れたように、学校での指導はちがいます↓
みてわかるとおり、学校の方法では、途中式がひとつ余計に必要です。
しかし+-の前で式を区切ることによって、途中式がひとつ少なくなります。
結果、計算スピードのUPにつながります。
また、学校の方法では、乗除計算の符号とかっこ外しの符号と、それぞれ別に考えなくてはなりません。
しかし+-の前で式を区切れば、すべて乗除計算の符号として、一発で考えることができます。
つまり、かっこ外しの本来の意味に沿った計算方法となるのです。
以上2点のメリットから、私はこの方法を採用しています。
そして、この方法を採用してから、次単元「文字と式」における下のようなミスが格段に減りました。
\begin{eqnarray} & & (2x-3y)-(4x-5y) \\ &=& 2x-3y-4x-5y \\ &=& -2x-8y \end{eqnarray}
これ、中学生がよくやるミスですが、私はこの式の後半を「じつは分配法則である」と言っています。
(詳しくは以下の記事を参照)

「+-の前で式を区切る」という四則計算方法に慣れていれば、おのずと、かっこ外しの本来の意味が乗法であると体得します。
だから、文字式のかっこ外しになっても、戸惑わないんです。
私自身、この方法を初めて教わったときは「なるほろ!」と口に出して言ってました。
おススメですので、ぜひ広めてほしいと思います。
>Amazonプライム・ビデオで「gifted/ギフテッド (字幕版)」を観る
分配法則でつまずく
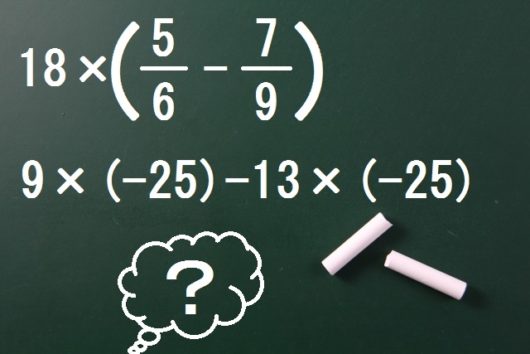
つづいて「正負の数」における計算単元の最後、分配法則です。
分配法則でつまずくパターンはおおきくわけて3つあります。
なので、どの原因でつまずいているか見極めて、それぞれの原因に沿った対応をすることが必要です。
原因
- 「これ、何の役に立つの?」で思考が止まってる
- 分配法則の計算に習熟しないまま、逆をやろうとしている
- 答えが100や200等になる計算を知らない
1.について。
じつは分配法則は小学4年生で習っています。
2020年度から全面実施される新学習指導要領でも、これは変わりません。(単元は「数量関係」から「数と計算」へと移行)
よって、計算しようとすればできるはずなのに、「うーん」と唸ったまま黙りこんでしまうような生徒。
こんな生徒の場合、「分配法則ってなんのために習うんだろう?」で思考が止まっている可能性があります。
こんな生徒には、分配法則が実際に役立つ場面を見せてあげるといいでしょう。
![]()
2.について。
分配法則の計算はできるのに、その逆の計算になると途端にわからなくなる。
こんな生徒をよく見かけます。
つまり、
\begin{eqnarray} & & (9-13) \times (-25) \\ &=& 9 \times (-25) -13 \times (-25) \tag{1} \end{eqnarray}
はできるのに、
\begin{eqnarray} & & 9 \times (-25) -13 \times (-25) \\ &=& (9-13) \times (-25) \tag{2} \end{eqnarray}
はできない場合です。
この場合はまず分配法則にじゅうぶん習熟させること、そして分配法則の逆をスムーズに導入することで解消にむかいます。
![]()
3.について。
式(2)に変形する所までは習熟しても、その先の
\begin{eqnarray} &=& -4 \times (-25) \\ &=& 100 \tag{2′} \end{eqnarray}
までたどりつけない生徒もいます。
こんな生徒は、かっこの中を先に計算して-4が出てきた瞬間、「あ!\(4 \times 25\) で\(100\) だ!」というひらめきができない。
つまり、計算して100や200ちょうどになる、そんな計算式のストックが頭の中にないのです。
よってこの場合には、計算式のストックを生徒の頭にインプットすることが必要になります。
指導案1
①上のような図で分配法則を伝えた後、以下のような例題を出す。
$$ 18 \times \left( \frac{5}{6} – \frac{7}{9} \right ) $$
②「ふつうにかっこの中から計算すると、こうだね」と言って、やってみせる。
\begin{eqnarray} &=& 18 \times \left( \frac{15}{18} – \frac{14}{18} \right ) \\ &=& 18 \times \frac{1}{18} \\ &=& 1 \end{eqnarray}
「でも、分配法則を使うと、こうなる」と言って、やってみせる。
\begin{eqnarray} &=& 18 \times \frac{5}{6} -18 \times \frac{7}{9} \\ &=& 15-14 \\ &=& 1 \end{eqnarray}
このとき、「2番目の式は書かなくてもできるように。約分は頭の中でする」と伝える。
③つづいて$$ \left( \frac{3}{4} – \frac{5}{6} \right ) \times (-24) $$ のような例を出し、質問しながら解いていく。
(「かけ算がうしろにあっても同じように分配法則できる」と一言伝える)。
「\( \frac{3}{4} \times (-24) \) 、符号はどっち?」「-」
「\(4\) と\(24\) で約分、何が残る?」「\(6\)」
「\( 3 \times 6 \) ?」「\(18\)」
→ \(-18\) と書く。
「\( – \frac{5}{6} \times (-24) \) 、符号はどっち?」「+」
「\(6\) と\(24\) で約分、何が残る?」「\(4\)」
「\( 5 \times 4 \) ?」「\(20\)」
→ \(+20\) と書く。
最後に計算させて、答えを書く。
\begin{eqnarray} & & \left( \frac{3}{4} – \frac{5}{6} \right ) \times (-24) \\ &=& -18+20 \\ &=& 2 \end{eqnarray}
④このように、かっこの中が分数などの場合、分配法則を使った方が速い、と伝える。
加えて「じつは中学数学ではこのあと分配法則が目白押し」とも伝える。
(どんな単元で分配法則を使うかは、注意点を参照)
同様の練習問題を一緒に解く。
生徒が計算に慣れてきたら、自分でさせる。
指導案2
①「分配法則の逆」の計算でつまずいている場合、まずは分配法則の計算を十分にさせる。
生徒が計算に慣れるまで、分配の矢印を書いてあげてもいい。
また分配先の符号&数字に下線を引いてあげてもいい。
②以下の例題を示し、分配させる。
$$ 13 \times (4+6) = 13 \times 4 +13 \times 6 \tag{1}$$
「じゃ、逆にこうしてもいいよね」と、以下の式を書く。
$$ 13 \times 4 +13 \times 6 = 13 \times (4+6) \tag{2}$$
「(1)はふつうの分配法則。(2)はその逆」。
③「(2)のつづきを計算するとこう」と言って、計算する。
\begin{eqnarray} &=& 13 \times 10 \\ &=& 130 \end{eqnarray}
「(1)のつづきを計算するのと、どっちがラク?」「(2)」
「こんなふうに、分配法則の逆を使うことで、計算がものすごくラクになる場合がある」。
④再び(2)の最初の式を書く。
そして「じゃあ、どうやればいいか?同じ数字を探せばいい」と伝える。
「この式のなかで同じ数字は?」「13」
以下のように囲む。
「そう、13がともにかけ算にある。これをまず書いて、横にかっこを書く」。
以下のように続ける。
「分配したら元の式に戻るように、かっこの中を考える」。
「前は?」「4」
「うしろは?」「6」「符号付きで」「+6」
そして分配したら元の式に戻ることを確認する。
あとはかっこの中を計算して、答えまで。
⑤負の数もある場合、共通因数が後ろにある場合でも例を示す。
「同じ数字は?」「-25」
「分配して元に戻るようにかっこの中を考える。前は?」「9」
「うしろは?」「-13」
「かっこの中を計算」「-4」
「最後まで計算」「100」
指導案3
①以上のように、分配法則の逆をするとキリのいい数字になることが多いと伝える。
ここで「ついでに」と前置きして、キリのいい結果になる計算をいくつか紹介する。
\begin{eqnarray} & & 6+4 \quad 4-14 \quad -8-12 \\ & & 93+7 \quad 105-5 \\ & & 25\times4 \quad 25\times8 \quad 20\times5 \end{eqnarray}
②例題をひとつふたつ示して、させてみる。
\begin{eqnarray} & & 25\times17 +25\times(-9) \\&=& 25\times (17-9) \\&=& 25\times8 \\&=& 200 \end{eqnarray}
「同じ数字は?」
「分配したら元に戻るように、かっこの中を考える」
「元に戻るか、それ?」
「かっこの中を計算」
「最後まで」
等の声かけを随時していく。
③同様の練習問題を一緒に解く。
生徒が計算に慣れてきたら、自分でさせる。
注意点
学力上位者で、「分配法則って何の役に立つの?」でつまずいていた生徒の場合、すこし先で分配法則を使う例をいくつか示してあげたほうがいいでしょう。
分配法則を使う主な単元は以下のとおりです。
○中1「文字と式」単項式×多項式など
$$ 3(2x-5y) \qquad \frac{-3a+5b}{6} \times (-18) $$
○中2「式の計算」分数計算など
$$ \frac{4x+6y}{7} – \frac{5x-8y}{3} $$
○中3「多項式」展開
$$ 2x(x-3) \qquad (4m-5n)(4m+7n) $$
また、分配法則の逆を使う主な単元は以下のとおり。
○中1「文字と式」計算の導入
\begin{eqnarray} & & 3x+2x \\&=& (3+2)x \\&=& 5x \end{eqnarray}
○中2「式の計算」式による説明
問)2桁の整数とその十の位と一の位の数を入れかえた整数の和は11の倍数になることを説明せよ。
\(m\) , \(n\) を整数とすると、2桁の整数は\(10m+n\) , 入れかえた整数は\(10n+m\) と表せる。
\begin{eqnarray} & & (10m+n)+(10n+m) \\&=& \underline{11m+11n} \\&=& \underline{11(m+n)} \end{eqnarray}
\(m+n\) は整数なので \( 11(m+n) \) は11の倍数である。
よって2桁の整数とその十の位と一の位の数を入れかえた整数の和は11の倍数になる。
○中3「多項式」因数分解
$$ 3x^2 -12x = 3x(x-4) $$
*各単元の内容はリンク先へ
なぜこの教え方か?
「正負の数」単元内であれば、分配法則を使わなくてもすべての問題が計算できます。
だから、「分配法則を使ったほうがラクな計算がある」だけでは、理由として弱い。
そこで私はフライング気味に、先で習う単元もすこし見せるようにしています。
なぜ分配法則を習うのか?
その本当の答えは「先の単元で必ず使うから」が正解だからです。
「これ、何の役に立つの?」という生徒には、ためらわずに先の単元を見せるといいでしょう。
また、学校では分配したあとの式を書かせる先生が多いようです。
つまり、\begin{eqnarray} & & 18 \times \left( \frac{5}{6} – \frac{7}{9} \right ) \\ &=& 18 \times \frac{5}{6} -18 \times \frac{7}{9} \\ &=& 15-14 \\ &=& 1 \end{eqnarray}
の2番目の式を「ちゃんと書きなさい」と指導される場合が多いのです。
しかし上述したように、私は約分は頭のなかでさせます。つまり、\begin{eqnarray} & & 18 \times \left( \frac{5}{6} – \frac{7}{9} \right ) \\ &=& 15-14 \\ &=& 1 \end{eqnarray}
と書かせるのです。
これも、以前の記事(加減、乗除)までで言ってきたように、先々のことを見据えた指導です。つまり、たとえば次単元「文字と式」におけるこんな計算で、\begin{eqnarray} & &24 \left( \frac{3}{4}a + \frac{5}{3}b \right ) \\&=& 24 \times \frac{3}{4}a +24 \times \frac{5}{3}b \\&=& 18a+40b \end{eqnarray} と書いていたら遅いんです。
2番目の式は省略して、\begin{eqnarray} & &24 \left( \frac{3}{4}a + \frac{5}{3}b \right ) \\&=& 18a+40b \end{eqnarray} といきなり出せるようじゃないと、テスト時間内に解き終わりません。
正確さを求めつつ、徐々に暗算でできるように導いていく。
中2、中3、高校生になっても数学のできる生徒にしたいなら、この姿勢は非常に大切です。
>Amazonプライム・ビデオで「gifted/ギフテッド (字幕版)」を観る
まとめ

○四則混合でつまずく生徒に…
計算の順序を示した後、+-の前で式を区切らせる。
かっこ内に計算がある場合は、かっこの中からすることを徹底する。
*「目の前でさせてみる」という過程をふむことで、こまかい注意点を生徒に落とし込むことができる。
○分配法則でつまずく生徒に…
「これ何の役に立つの?」で思考が止まっている場合、かっこ内に分数のある計算を示して有用性を共有する。くわえて、先の単元で分配法則を使う例をいくつか見せてあげる。
分配法則の逆ができない場合、まず分配法則の計算に習熟させる。そのうえで、「同じ数字を探す」「分配したら元に戻るようにかっこの中を考える」とアドバイスする。
分配法則の逆の計算が最後までいかない場合、\( 25\times4 \) などキリのいい結果になる計算を暗記させる。
*分配したあとの約分は暗算でさせること。先々を見据えたら、正確性だけじゃなく計算スピードも大切だから。
この記事は管理人のジュウゴが、過去の経験といろんな書籍情報をもとに書いています。
今後のさらなる経験や情報によって、改訂されていく余地アリです。
よって教育に携わる方からのご意見・ご感想は大歓迎です。
下のコメント欄から、随時おまちしています。



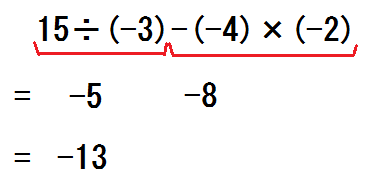


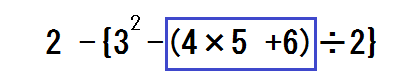

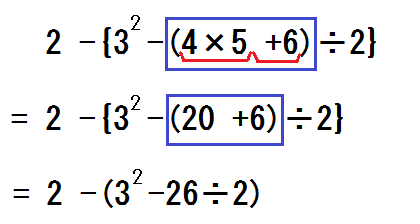
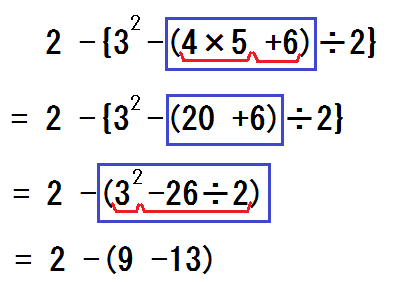
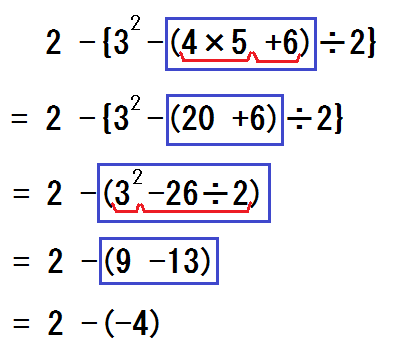
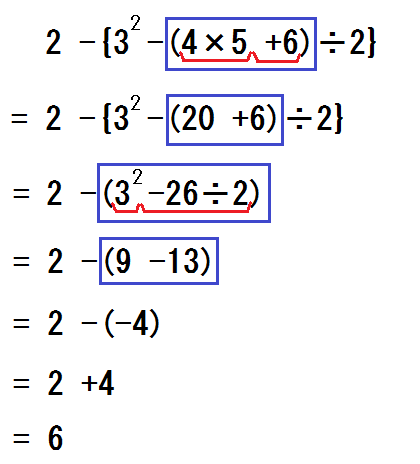






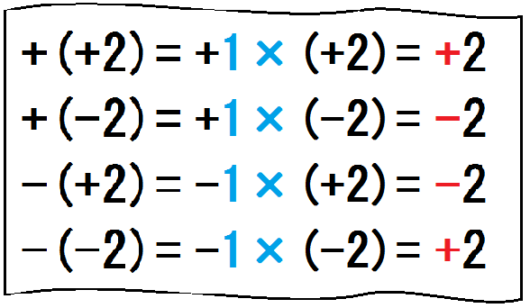
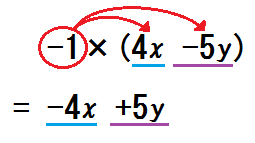

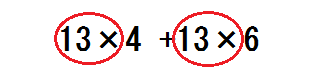
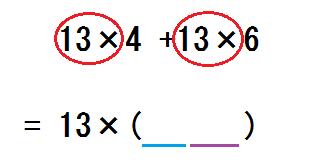
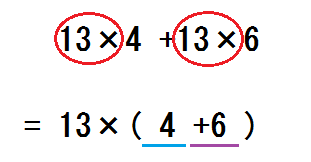
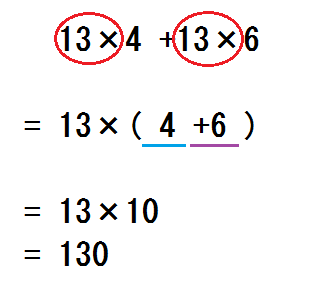
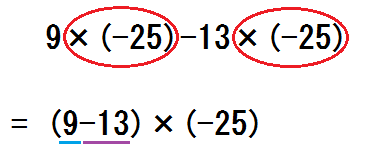
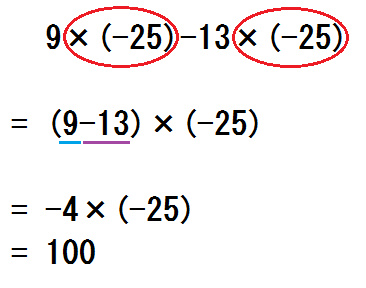


コメント
初めまして。
五年前、長女が中一の数学でつまずいたのをきっかけにじゅうごさんのサイトにたどり着きました。
今年中学に上がる長男が躓かないようにと、春休みを利用してまたこちらの指導方法にお世話になってます。
「足すとプラス」、「引くとマイナス」の違いがわからない!と困惑していた子供。じゅうごさんの指導にありますようにすべてプラスとマイナスで言い換えて教えています。
私自身は中学数学が好きでまったく困らなかったのですが、こちらのサイトを見てどうして子供が数学を理解できないのか、勉強なりました。
他の分野も大変役に立ち、わかりやすいので活用させていただいています。
「(かっこの外にある)+-の前で式を区切る」。
この方法いいですね。
とある授業動画を見てみましたが、
+-の「前」で式を区切る方法と、+-の「後」で式を区切る方法とが混在しており、
わかりにくい、と感じました。
自分自身の教え方もそうであったと反省です。
+-の「前」で式を区切る方法に統一しようと思います。
なお、最初の「注意点」の、最初の式(答えが「-38」になる式)は、
冒頭に「ー」が抜けているのではないかと思われます。
ご確認ください。
冒頭のマイナス、抜けていました。
ありがとうございます、さっそく修正します。