中学数学のつまずき解消をめざすこの連載。
今回から中3数学「多項式」という単元に入ります。
1回目はまず展開の基本から。
中学生に展開を教える場合、どんな流れで、どこに注意して教えればいいのか、そのノウハウを共有します。
塾講師や家庭教師、保護者の方はぜひ参考にしてください。
≪「多項式」の記事一覧≫
展開とは何か

中3生に展開を指導するときには、まず展開とは何かをわかりやすく伝える必要があります。
また、いきなり多項式×多項式( \((a+b)(c+d)\) など)を教えるのではなく、中1・中2の計算からとくに4項目を復習しておくと、その後の学習がスムーズになります。
以下、指導例を見ていきましょう。
指導例:復習その1
展開とは、カッコを外すこと。
たとえばこんな問題のカッコを外すこと↓
復習1)次の式を展開しなさい。
$$ -2x(x-3y) $$
この問題、どうやってかっこを外せばよかった?
そう、分配法則だね。
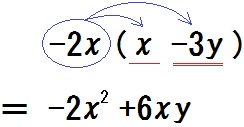
このように、「式を展開しなさい」って言われたら分配法則を使ってカッコを外す。
これが基本。
すでに中1・中2で習ったね。
ちなみに分配するときには、\(-2x\) を \(x\) と \(-3y\) にかけること。
つまり項をかたまりで捉えること。
ここ、注意しよう。
指導例:復習その2
じゃ、復習ついでにあと3問、いっしょにやってみよう。
復習2)次の式を展開しなさい。
$$ 6a^2 (ab+2a-3b) $$

このように、カッコ内に項が3つ以上あっても分配できたね。
復習3)次の式を展開しなさい。
$$ (x^3 -5x^2) \times (-x) $$
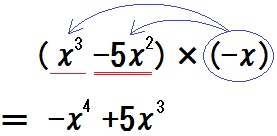
このように、うしろからでも分配できたね。
復習4)次の式を展開しなさい。
$$ 3(a-5b) -4(2a-b) $$

このように、カッコを外したあとも計算できるところは計算するんだったね。
以上、復習おわり。
展開とは分配法則とか使ってカッコを外すこと。
その際の注意点は
- 項をかたまりで捉える
- カッコ内に項が3つ以上あっても分配できる
- うしろからでも分配できる
- カッコを外したあとも計算できるところは計算する
この知識をつかって、中3の内容に入っていくよ。
指導上の注意点
上記4つの注意点のうち、いちばん大切なのは「項をかたまりで捉えること」です。
このサイトでは、中1「正負の数」の最初から、項をかたまりで捉えるよう教えています。
しかし中には、項のかたまりという意識を持たないまま中3になった生徒もいるでしょう。
そこで指導例では、項にしるしを付けました。
この方法は意外と幅広い生徒に有効です。
だって、計算の得意な子でも、中2の後半はずっと図形と確率ばかりやってきて「項のかたまり」という意識が薄れていることが多いから。
ぜひ使ってください。
[関連記事]
中学数学「文字と式」でつまずく原因と解決法② 途中式と分数、かっこ外し、分配法則
またこの指導例には、わり算の分配問題は載せていません。
つまり
$$ (4 x^2 y -8 x y^2) \div \left(- \frac{2}{3} xy \right) $$
↑こんな問題は省きました。
理由は、このあとの多項式×多項式の内容に直接つながらないからです。
もちろん学力に余裕のある生徒にはさせてください。
ただ、計算力の低い子・数学の苦手な子には、とばしてかまいません。
あるいは「ついでにこいつもやっとこうか」と、いっしょにサッと片付けちゃってください。
中学生がつまずかないためには、何を教えるべきかだけじゃなく、何を教えないかも考える。
ジュウゴが大切にしている姿勢のひとつです。
多項式×多項式の展開

次に、中3新内容である多項式×多項式の展開に入ります。
ここでジュウゴは、展開する方法だけでなく、なぜそんな方法になるのかの理解まで説明しています。
指導例:導入
では、新しい内容に入ります。
こんな式を展開してみよう↓
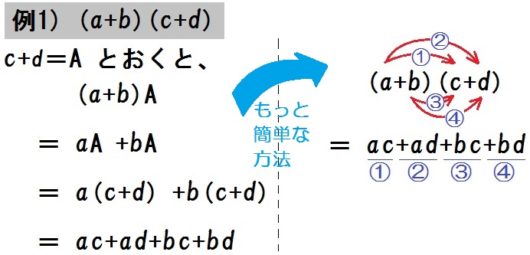
例題1)次の式を展開しなさい。
$$ (a+b)(c+d) $$
これ、いままでのようにはカッコを外せない。
そこでちょっとした工夫をします。
よく見ててね。

うしろの \(c+d\) をひとまとまりにして、なんでもいいけどとりあえず大文字Aと置いてみた。
すると、\( (a+b)A \) という式はうしろから分配できる。

ここで大文字Aを元の \(c+d\) に戻す。
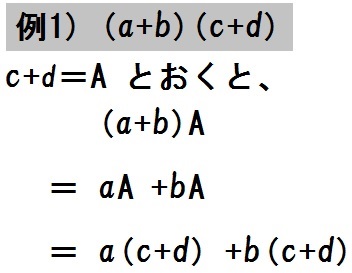
あとは \(a\) と \(+b\) がそれぞれ分配できるね。

こうして、\((a+b)(c+d)\) のような(多項式)×(多項式)の計算は
\begin{eqnarray} & & (a+b)(c+d) \\ &=& ac+ad+bc+cd \end{eqnarray}
と展開できるんだ。
指導例:方法の理解
でも、以上の計算ってめんどくさいよね。
そこでもっとカンタンな方法はないか、展開した結果から考えてみよう。

① \(ac\) は \(a\) と \(c\) をかけたもの。
② \(+ad\) は \(a\) と \(+d\) をかけたもの。
③ \(+bc\) は \(+b\) と \(c\) をかけたもの。
④ \(+bd\) は \(+b\) と \(+d\) をかけたもの。
つまり、こういうことだ↓
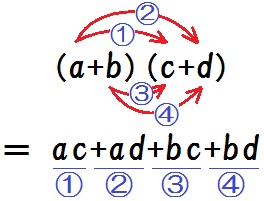
ここから、(多項式)×(多項式)の展開の方法がわかる。
(多項式)×(多項式)は
- 前と前
- 前と後
- 後と前
- 後と後
と順番にかけ算すればいいんだと。
理解できた?
じゃ、以上を書き写して。
指導例:一緒に類題
書き写せたら、類題を一緒に解いてみよう。
類題1-1)次の式を展開しなさい。
$$ (a+b)(c-d) $$
\(a\) と \(c\) をかけて?→ \(ac\)
\(a\) と \(-d\) をかけて?→ \(-ad\)
\(+b\) と \(c\) をかけて?→ \(+bc\)
\(+b\) と \(-d\) をかけて?→ \(-bd\)

(以下も同様の手順で。)
類題1-2)次の式を展開しなさい。
$$ (a-b)(c+d) $$
類題1-3)次の式を展開しなさい。
$$ (a-b)(c-d) $$

もちろん \(a,b\) だけじゃなく \(x,y\) や数字があっても同じ。
例題2)次の式を展開しなさい。
$$ (x+3)(y+2) $$
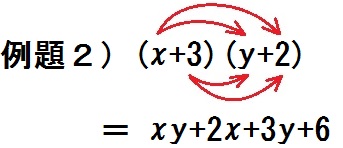
また、カッコ内に項が3つ以上あっても、順番にかければいいだけだ。
例題3)次の式を展開しなさい。
$$ (x-4)(y-z+5) $$
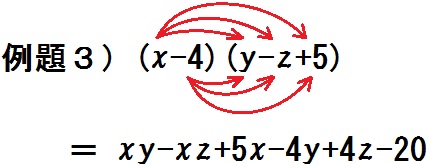
これで(多項式)×(多項式)の展開のやり方はわかったね。
じゃ、練習問題をたくさん解いて「わかる」を「できる」にしていこう。
指導上の注意点
ここでの注意点は3つです。
1つ。
(多項式)×(多項式)の展開方法がなぜ出てくるのかの説明までちゃんと行うこと。
ジュウゴの経験上、たとえ偏差値40以下の中学生でも、わかりやすく説明すれば理解してくれます。
公式や方法がどこから来るのか理解すれば深く記憶に残るので、教えたほうがいいでしょう。
ちなみに大文字で置き換えるという工夫も今後、展開の応用問題や因数分解の応用問題で出てきます。
2つ。
符号まで含めて言うこと。
つまり
「 \(a\) と \(d\) をかけて」じゃなく
「 \(a\) と \(+d\) をかけて」というように言うこと。
理由は、項をひとかたまりと捉えることが大切だからです。
場合によっては、ここでも項ごとに下線を引いてもいいでしょう。
3つ。
練習問題をさせるとき、慣れてきたと思ったら矢印は無くすこと。
いつまでも書いていたら時間がかかりすぎるからです。
以上3つの点に注意して、中3の展開を導入してあげてください。
多項式×多項式の展開その2

最後に、乗法公式に入る前の「展開の応用問題」を扱います。
応用問題とは
- 展開してさらに同類項をまとめる問題
- 同類項が2種類以上ある問題
- 分数のある問題
の3つです。
指導例:最後まで計算する
では、ちょっと応用問題。
例題4)次の式を展開しなさい。
$$ (2a-3)(3a+2) $$
おなじように展開してみよう。
\begin{eqnarray} & & (2a-3)(3a+2) \\ &=& 6a^2 +4a -9a -6 \end{eqnarray}
じつはこの問題、これで終わりじゃない。
まだすることがあるんだ。何だと思う?
そう、\(+4a\) と \(-9a\) が計算できるね!
\begin{eqnarray} & & (2a-3)(3a+2) \\ &=& 6a^2 +4a -9a -6 \\ &=& 6a^2 -5a -6 \end{eqnarray}
ここまで計算して答え。
つまり展開したあとも計算できるところは計算すること。
忘れずにね。
じゃ例題4をもういちど自分でやってみて。
指導例:仕上げ
あと2問、一緒にやってみよう。
例題5)次の式を展開しなさい。
$$ (x-2)(x^2 -x -1) $$
\begin{eqnarray} & & (x-2)(x^2 -x -1) \\ &=& x^3 -x^2 -x -2x^2 +2x +2 \\ &=& x^3 -3x^2 +x +2 \end{eqnarray}
このように、同類項が2種類以上あってもそれぞれ計算してまとめること。
ちなみに \(-x^2\) と \(-x\) は同類項じゃないからね。注意しよう。
[関連記事]
中1数学「文字と式」① 文字式計算の導入
例題6)次の式を展開しなさい。
$$ \left( 2x + \frac{1}{6} \right) \left( 3x – \frac{2}{5} \right) $$
\begin{eqnarray} & & \left( 2x + \frac{1}{6} \right) \left( 3x – \frac{2}{5} \right) \\ &=& 6x^2 – \frac{4}{5}x + \frac{1}{2}x – \frac{1}{15} \\ &=& 6x^2 – \frac{8}{10}x + \frac{5}{10}x – \frac{1}{15} \\ &=& 6x^2 – \frac{3}{10}x – \frac{1}{15} \end{eqnarray}
このように、たとえ分数が出てきても計算できるところは計算すること。
ちなみに3行目の通分した式はちゃんと書こうね。
「分数計算は暗算でイケる!」ってやってると、けっこう間違えること、進学校の高校生でもよくあるから。
[関連記事]
中1数学「文字と式」② 途中式と分数、かっこ外し、分配法則
これで展開の基本はおしまい。
いっぱい練習問題を解いて「わかる」を「できる」にしていこう。
指導上の注意点
ここでの注意点は2つです。
1つ。
例題5で、同類項の見分けがつかない生徒には、しるしをつけるといい。
「中3になっていまさら」と思うかも知れませんが、子どものなかには学力とは関係なく似たような文字の見分けがつきにくいという脳をもった子が一定数います(LDとはちょっとちがう)。
しるしをつけることでできるようになるなら、ぜひその工夫を伝えてあげてください。

2つ。
例題6で、分数の通分を余白にちょこちょこ書かせないこと。つまり式のなかに計算も書くこと。
数学教育に携わる方なら必ず出会ったことがあるでしょう、ノートの余白にちいさく計算を書いて式自体は一行ですませようとする子。
なぜこの姿勢を直したほうがいいのか?
高校数学でつまずくからです。
高校数学では長い計算式をつなげていって、最終的に答えにたどりつきます。いっぱつで答えが出るなんてほとんどありません。
たとえば以下の計算は三角形の面積を求める公式7選という記事に書いた、ヘロンの公式の導出です。
△ABCにおいて、余弦定理より
$$ \cos A = \frac{b^2 +c^2 -a^2}{2bc} $$
\( \sin A\) >0より
\begin{eqnarray} \sin A &=& \sqrt{1- \left( \frac{b^2 + c^2 -a^2}{2bc} \right) ^2} \\ &=& \sqrt{ \frac{(2bc)^2 – (b^2 +c^2 -a^2)^2}{(2bc)^2}} \\ &=& \frac{1}{2bc} \sqrt{ \{2bc + (b^2 +c^2 -a^2) \} \{2bc – (b^2 +c^2 -a^2) \}} \\ &=& \frac{1}{2bc} \sqrt{ \{(b+c)^2 – a^2 \} \{a^2 – (b-c)^2 \}} \\ &=& \frac{1}{2bc} \sqrt{(b+c+a)(b+c-a)(a+b-c)(a-b+c)} \quad \mbox{…①} \end{eqnarray}
ここで \(a+b+c=2s\) とすると
\begin{eqnarray} b+c-a&=& 2s-2a = 2(s-a) \\ a+b-c&=& 2s-2c = 2(s-c) \\ a-b+c&=& 2s-2b = 2(s-b) \end{eqnarray}
よって①は
\begin{eqnarray} & & \frac{1}{2bc} \sqrt{2s \cdot 2(s-a) \cdot 2(s-c) \cdot 2(s-b)} \\ &=& \frac{2}{bc} \sqrt{s(s-a)(s-b)(s-c)} \end{eqnarray}
したがって、\(S= \frac{1}{2}bc \sin A\) より
\begin{eqnarray} S &=& \frac{1}{2} bc \cdot \frac{2}{bc} \sqrt{s(s-a)(s-b)(s-c)} \\ &=& \sqrt{s(s-a)(s-b)(s-c)} \end{eqnarray}
こんな途中式が高校で待ち受けてる!
だから余白にべつに計算なんて書くな、かならず式のなかで計算しろ!
って伝えてあげてください。
*高校数学の公式に関しては、以下の記事でも「加法定理」の導出をしています。参考までに。
三角比はいまどんな職業で役に立っているか?地図製作を例に解説する
まとめ

展開とはカッコを外すこと。
分配法則を使うのが基本。
(多項式)×(多項式)の展開は前から順にかけていく。
計算できるところは最後まで計算するのを忘れずに。
以上!
次回は乗法公式3つをそれぞれ解説します。
とくに、因数分解へスムーズにつなげるにはどのレベルまでできるようにしたらいいか、という観点を重視してお伝えする予定です。
NEXT→中学数学「多項式」の教え方② 乗法公式
≪「多項式」の記事一覧≫




コメント