中学数学「多項式」の教え方⑥ 式の計算の利用

中３数学「多項式」のさいごは、式の計算の利用を解説します。

式の計算の利用には、5種類の問題があります。

• 展開を利用した計算
  （例：\(52^2 \) を工夫して計算せよ）
• 因数分解を利用した計算
  （例：\(29^2 -21^2\) を工夫して計算せよ）
• 式の値
  （例：\(x=96\) のとき \(x^2 +3x-4\) の値を求めよ）
• 整数の性質の証明
  （例：連続する２つの奇数の積に１をたした数は４の倍数になることを証明せよ）
• 図形の性質の証明
  （ \(S=al\) のやつ）

このうち大切なのは「式の値」「整数の性質の証明」「図形の性質の証明」の３つです。

なぜならこの３つが高校入試や高校数学につながるから。

ってことで、

○式の値
○整数の性質の証明
○図形の性質の証明

この３問題それぞれの解き方を

• 高校入試でよく出る問題→基本
• 高校数学につながる問題→難問

と分けて、わかりやすく解説していきます。

基本問題は全員向け、難問は成績上位者向けです。

中学生のみならず、指導者・保護者の方も指導案としてご参考ください。

式の値（基本）

まず式の値の基本から。

中２でもやりましたね、

「式の値を求めよ」と言われたら、代入するんだと。

んで式を変形してから代入したほうが計算ラクだと。

やり方

「式の値を求めよ」と言われてるので、
\(x=29 , y=2\) を式に代入したらいい。

ただ、そのまま代入したら↓
\( (29 -2 \times 2)^2 -(29-2) \times (29- 8 \times 2)\)
これ、計算がたいへん。

そこで例題1-1は、式を展開してから代入しよう。

\begin{eqnarray} & & (x-2y)^2 -(x-y)(x-8y) \\ &=& x^2 -4xy+4y^2 -(x^2 -9xy+8y^2) \\ &=& x^2 -4xy+4y^2 -x^2 +9xy-8y^2 \\ &=& 5xy-4y^2 \\ & & x=29 , y=2 \mbox{ を代入して} \\ &=& 5 \times 29 \times 2 -4 \times 2^2 \\ &=& 290-16 \\ &=& 274 \end{eqnarray}

答．274

[関連記事]
中学数学「多項式」の教え方③ 展開の応用問題

 

この問題も \(x=96\) を代入したらいい。

でも、そのまま式に代入したら↓
\( 96^2 +3 \times 96 -4\)
となって、やっぱり計算がたいへんだ。

だから例題1-2も、式を変形してから代入したほうがラク。

展開は、もうしてある。

何したらいいと思う？

そう、因数分解だ！

\begin{eqnarray} & & x^2 +3x-4 \\ &=& (x+4)(x-1) \\ & & x=96 \mbox{ を代入して} \\ &=& (96+4) \times (96-1) \\ &=& 100 \times 95 \\ &=& 9500 \end{eqnarray}

答．9500

このように、式の値を求めるときには、式を展開したり因数分解したりしてから代入すると計算がラクなんだ。

[関連記事]
中学数学「多項式」の教え方④ 因数分解

 

注意点

式の値の基本では、２つのことに注意しましょう。

１つ。
展開や因数分解の計算にじゅうぶん慣れてから式の値に入ること。

そうでないと、ここでつまずきます。

例題1-1の計算ができない。

例題1-2の式をみて「因数分解できる」と気づかない。

そんな中学生は、展開や因数分解の練習をたくさん積んでから再度ここにもどってきましょう。

[関連記事]

• 中学数学「多項式」の教え方② 乗法公式
• 中学数学「多項式」の教え方③ 展開の応用問題
• 中学数学「多項式」の教え方④ 因数分解
• 中学数学「多項式」の教え方⑤ 因数分解の応用問題

 

２つ。
数字を代入した式をちゃんと書くこと。

つまり \(5xy-4y^2\) に
\(x=29 , y=2\) を代入しただけの式↓
「 \(5 \times 29 \times 2 -4 \times 2^2\) 」

これ、ちゃんと書くこと。

なぜなら、これ書かない生徒ほどよく計算ミスするからです。

そんな生徒は、代入するという行為と計算するという行為を一行ですませようとしてるので、計算力の高い生徒でも高確率でミスします。

代入直後の式はちゃんと書くようにしましょう。

 

ちなみに例題１の問題は、式を変形しなくてもどうにか解けました。

しかし、これから紹介するのは式変形しないとできない問題です。

 

式の値（難問）

例題２は公立高校入試ではまず出ません。

私立入試や、高校数学で出る難問です。

よって、この問題のやり方はちょっとくわしく説明します。

やり方（準備）

例題２を解くまえに、準備をしよう。

以下３つの問題をやってみて。

\begin{eqnarray} & & x+y=6 \mbox{ を代入して} \\ &=& 6^2 \\ &=& 36 \end{eqnarray}

\begin{eqnarray} & & x^2 +2xy+y^2 \\ &=& (x+y)^2 \\ & & x+y=6 \mbox{ を代入して} \\ &=& 6^2 \\ &=& 36 \end{eqnarray}

\begin{eqnarray} & & x+y=6 , xy=4 \mbox{ を代入して} \\ &=& 6^2 -2 \times 4 \\ &=& 36-8 \\ &=& 28 \end{eqnarray}

よくできた！

ところで、３つめの問題の式は、展開すると

\begin{eqnarray} & & (x+y)^2 -2xy \\ &=& x^2 +2xy+y^2 -2xy \\ &=& x^2 +y^2 \end{eqnarray}

となる。

じゃあ、逆にこんな式変形もできる↓

\begin{eqnarray} & & x^2 +y^2 \\ &=& x^2 +2xy+y^2 -2xy \\ &=& (x+y)^2 -2xy \end{eqnarray}

おなじ理屈で、こんな式変形ができるのもわかるかな↓

\begin{eqnarray} & & x^2 +9y^2 \\ &=& x^2 +6xy+9y^2 -6xy \\ &=& (x+3y)^2 -6xy \end{eqnarray}

\begin{eqnarray} & & x^2 + \frac{1}{x^2} \\ &=& x^2 +2+ \frac{1}{x^2} -2 \\ &=& \left( x+ \frac{1}{x} \right)^2 -2 \end{eqnarray}

つまり、何をしたか？

• 「前うしろかけて２倍」（ \(+2xy\) や \(+6xy\) や \(+2\) ）を追加して、
  ムリヤリ \( ( \qquad )^2 \) の形にもっていけるようにした。
• ただ追加しただけじゃ＝にならないんで、
  うしろに引き算しといた（ \(-2xy\) や \(-6xy\) や \(-2\) ）。

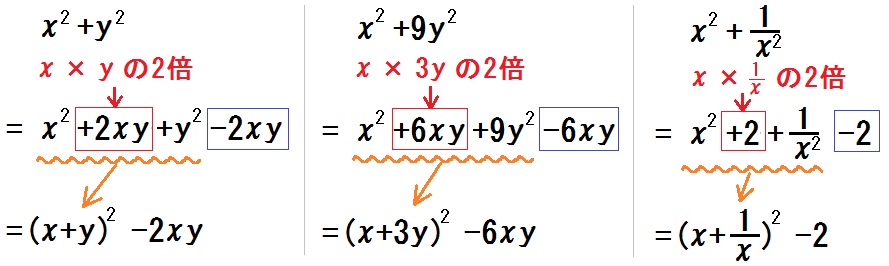
この式変形が理解できれば、例題２が解けます。

 

やり方（解法）

この問題の式、このままじゃ代入できない。

そこで準備でやった式変形をする。

\(x^2\) の元は → \(x\)
\(y^2\) の元は → \(y\)
前うしろかけて２倍は → \(2xy\)

よって、

\begin{eqnarray} & & x^2 +y^2 \\ &=& x^2 +2xy+y^2 -2xy \\ &=& (x+y)^2 -2xy \\ & & x+y=6 , xy=4 \mbox{ を代入して} \\ &=& 6^2 -2 \times 4 \\ &=& 36-8 \\ &=& 28 \end{eqnarray}

答．28

 

例題2-1と同様だ。

\(x^2\) の元は → \(x\)
\(\frac{1}{x^2}\) の元は → \(\frac{1}{x}\)
前うしろかけて２倍は → \(2\)

よって、

\begin{eqnarray} & & x^2 + \frac{1}{x^2} \\ &=& x^2 +2+ \frac{1}{x^2} -2 \\ &=& \left( x+ \frac{1}{x} \right)^2 -2 \\ & & x+ \frac{1}{x} =3 \mbox{ を代入して} \\ &=& 3^2 -2 \\ &=& 9-2 \\ &=& 7 \end{eqnarray}

答．7

このように、

「 \(x+y= \mbox{○}\) のとき \( x^2 + y^2 \) の値を求めよ」なんて問題が出たら、ムリヤリ \( ( \qquad )^2 \) の形に変形すること。

 

注意点

さきほども言ったとおり、例題２のような問題は問題集のラストや、テスト・模試の発展問題、そして難関私立の入試としてのみ出題されます。

よって、全員にさせる必要はありません。

「学校の内容はバッチリで、ほかの人と差をつけたい」という成績上位者のみ、やってみてください。

 

ただ成績上位者であっても、計算力がそこまで高くない中学生はむずかしがる傾向にあります。

一般に成績上位者というのは

• 計算力をふくめてすべての能力が高い
• 国語力の高さで他教科をカバーしている

という２タイプがいます。

後者の生徒には、ここで紹介した指導の流れをじっくり・ゆっくり・ていねいに行うことをおススメします。

ときに「ん？」と立ち止まったら、その子が理解するまでしんぼうづよく待つ。

たまにアドバイスもしてあげる。

そんで類題をもっと解く。

そうすることで習熟していけるでしょう。

 

では次に「整数の性質の証明」を解説します。

• 基本：式による証明問題
• 難問：商と余りの関係の問題

と分けてます。

＞次ページ：整数の性質の証明