中3「多項式」⑥ 式の計算の利用。
「式の値」「整数の性質の証明」ときて、ラストは「図形の性質の証明」です。
基本・難問のやり方をそれぞれわかりやすくまとめました。
図形の性質の証明(基本)

この問題のように、\(S=al\) という等式を証明せよ、と言われたら。
- \(S\) を文字で表して計算していく…①
- \(al\) も文字で表して計算していく…②
- ①と②がまったく同じ形になったら終了
という流れで証明できます。
そして、この問題の面積 \(S\) や長さ \(l\) といった複雑な図形を表すには
- 分けて、足す
- 大きく求めて、引く
という2パターンの考え方を使えばいい、というのはこの連載でずっと言ってきましたね。
やり方
例題5)下図のように、1辺の長さが \(p\) の正方形の土地のまわりに、幅 \(a\) の道がついている。この道の面積を \(S\) 、道のまんなかを通る線の長さを \(l\) とするとき、\(S=al\) となることを証明せよ。
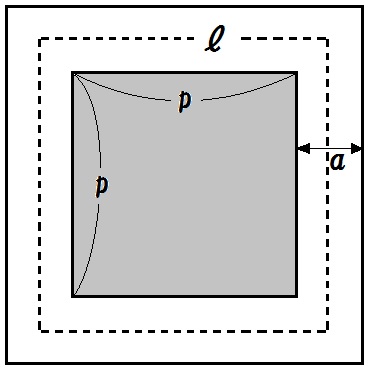
【考え方】
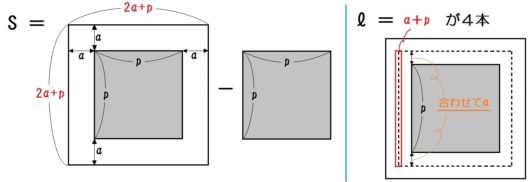
道の面積 \(S\) =大きな正方形-小さな正方形
線の長さ \(l\) = \(a+p\) が4本

【証明】
道の面積 \(S\) は
\begin{eqnarray} S &=& (2a+p)^2 -p^2 \\ &=& 4a^2 +4ap+p^2 -p^2 \\ &=& 4a^2 +4ap \ \mbox{…①} \end{eqnarray}
線の長さ \(l\) は
\begin{eqnarray} l &=& (a+p) \times 4 \\ &=& 4a+4p \end{eqnarray}
よって
\begin{eqnarray} al &=& a(4a+4p) \\ &=& 4a^2 +4ap \ \mbox{…②} \end{eqnarray}
①②から
$$ S=al $$
[関連記事]
注意点
中3生が \(S=al\) 問題でつまずくいちばんのポイントは、\(S\) や \(l\) を文字で表せないというところです。
なぜ表せないかというと、上に示したような図を自分でかかないから。
つまり、式を書き出すまえに頭を整理するための図をかく、この作業を怠っているからです。
「こーゆー図は先生が解説するためにかくもので、自分がやるときには関係ない」と思っているからです。

Sとlを求めるための図
だから、\(S=al\) 問題ができるようになりたいなら、余白に自分で図をかくこと。
分けて足す/大きく求めて引く のどっちかを使って、\(S\) と \(l\) を表そうとしてみること。
それを繰り返せばそのうち
「\(S\) は大きな正方形-小さな正方形だ」
「じゃ、それぞれの正方形の一辺を文字で表せばいい」
「大きな正方形の一辺は、\(p\) と、\(a\) が2つ」
「よし、一辺の長さが \(2a+p\) と表せた!図にかいておこう」
「これで大きな正方形の面積も \((2a+p)^2\) とわかる」
というようになってきます。
式を書き出すまえに、\(S\) と \(l\) を求めるための図を自分でかく。
このコツは次の難問でも活きてきます。
ちなみに上の「やり方」では \(l\) をいったん計算してから \(al\) を計算しましたが、慣れている生徒はいきなり \(al= a \{ (a+p) \times 4 \} = \mbox{…} \) 等とやってもOKです。
図形の性質の証明(難問)
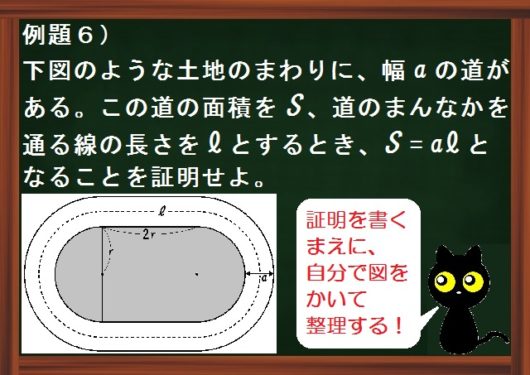
例題6も証明のやり方は基本とおなじ。
ただ円が混じっているというだけです。
ぜひ自力でチャレンジしてみてください。
やり方
例題6)下図のような土地のまわりに、幅 \(a\) の道がある。この道の面積を \(S\) 、道のまんなかを通る線の長さを \(l\) とするとき、\(S=al\) となることを証明せよ。
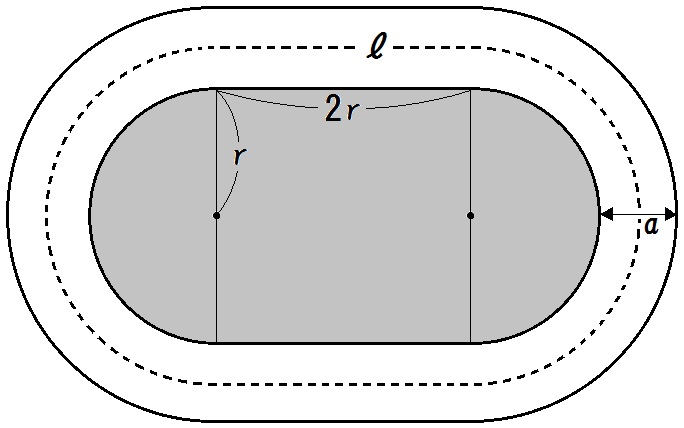
【考え方】
いろんな考え方ができるが、たとえばこんなかんじ↓
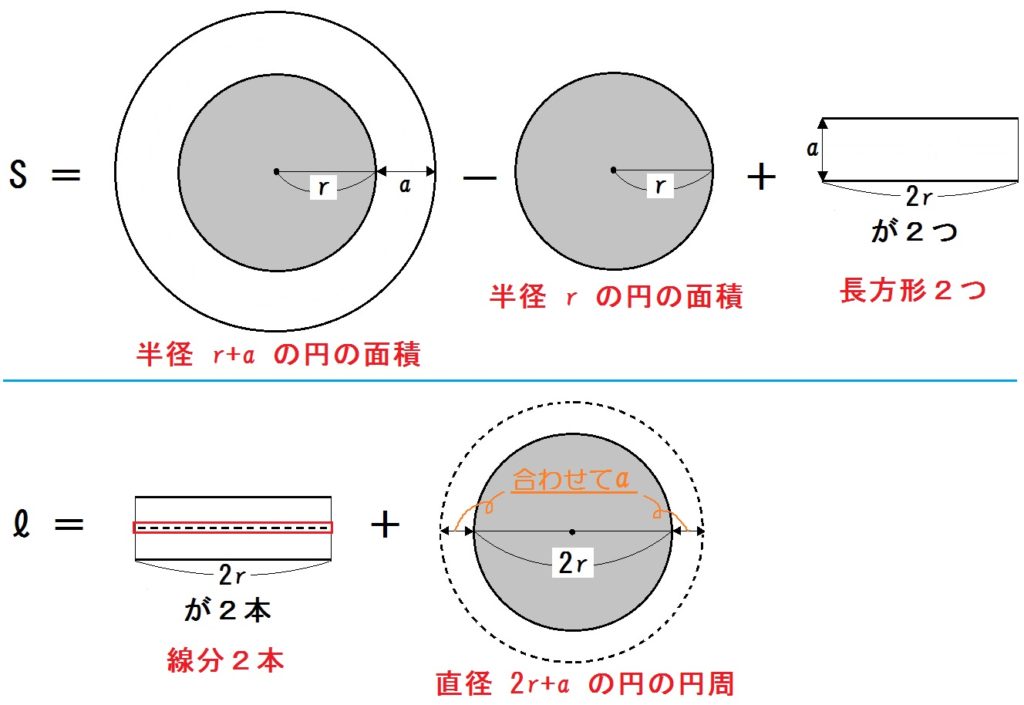
【証明】
\begin{eqnarray} S &=& \pi (r+a)^2 – \pi r^2 + a \times 2r \times 2 \\ &=& \pi (r^2 +2ar+a^2) – \pi r^2 +4ar \\ &=& \pi r^2 +2 \pi ar + \pi a^2 – \pi r^2 +4ar \\ &=& 4ar +2 \pi ar + \pi a^2 \ \mbox{…①} \end{eqnarray}
\begin{eqnarray} l &=& 2r \times 2 + \pi (2r+a) \\ &=& 4r +2 \pi r + \pi a \end{eqnarray}
よって
\begin{eqnarray} al &=& a(4r +2 \pi r + \pi a) \\ &=& 4ar +2 \pi ar + \pi a^2 \ \mbox{…②} \end{eqnarray}
①②から
$$ S=al $$
[関連記事]
注意点
最後の難問は、円が入ってて \(\pi\) があってややこしいというだけでした。
あんまり高校数学とはつながりません、ごめんなさいm(_ _)m
お詫びに、高校数学につながる話をひとつ。
一般に「等式 \(A=B\) を証明せよ」と言われたら、やり方は3パターンあります。
- \(A=\)■、\(B=\)■、ほら同じ形になったよ。
- \(A\) を変形して \(B\) にする、あるいは \(B\) を変形して \(A\) にする。
- \(A-B=0\) になることを示す。
この記事の証明では、パターン1を使いました。
でもパターン2、パターン3の方法でも、証明はできます。
先生や問題集によっては
- パターン2:\(S\) を変形して \(al\) にする。
(あるいは \(al\) を変形して \(S\) にする) - パターン3:\(S-al=0\) を示す。
という別の方法で証明していることもあります。
等式の証明には3パターンあるんだと押さえておくと、いらぬ混乱をしなくていいでしょう。
[関連記事]
数学の証明ってなに?なんで証明するの?なぜ文字を使うの?
まとめ

おつかれさまでした。
中3多項式 式の計算の利用。
ポイントをまとめます。
≪式の値≫
基本:式を展開したり因数分解したりしてから代入する。
難問:「 \(x+y= \mbox{○}\) のとき \( x^2 + y^2 \) の値」などの問題はムリヤリ \((\qquad)^2\) の形をつくる。
注意点:数字を代入した式をちゃんと書くこと。
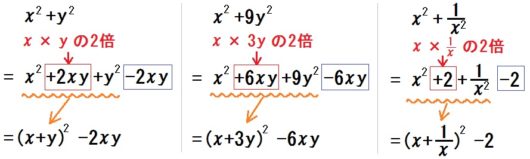
≪整数の性質の証明≫
基本:以下の4手順でやる。
- 登場人物を文字で表す
- 文章どおりに計算
- 結論の形にムリヤリもっていく
- 〆のことば
難問:商と余りの問題では、(割られる数)=(割る数)×(商)+(余り) という関係式を使う。
注意点:商と余りの問題では、数字部分もできるだけ割る数でくくること。

≪図形の性質の証明≫
基本:複雑な図形を表すには「分けて足す」あるいは「大きく求めて引く」。
難問:等式の証明の方法は3パターンある。
注意点:証明の式を書き出すまえに、\(S\) と \(l\) を求めるための図を自分でかくこと。
Sとlを求めるための図
これにて中3多項式は終わり!
次回からは平方根に入る予定です。
質問やご意見・ご要望などはコメント欄からどうぞ。
NEXT→中学数学「平方根」のコツ① 平方根とは/平方根の大小
≪「多項式」の記事一覧≫
- 中学数学「多項式」の教え方① 展開の基本
- 中学数学「多項式」の教え方② 乗法公式
- 中学数学「多項式」の教え方③ 展開の応用問題
- 中学数学「多項式」の教え方④ 因数分解
- 中学数学「多項式」の教え方⑤ 因数分解の応用問題
- 中学数学「多項式」の教え方⑥ 式の計算の利用



コメント