中1数学「比例と反比例」の教え方5回目。
今回は座標平面の導入と、比例・反比例のグラフについて解説します。
いきなりですが、中学生が座標およびグラフでつまずく原因はおもに2つ。
- 座標平面を図形的に扱うことに慣れていない
- 「グラフは点の集まり」という意識が育ってない
つまり、グラフに入る前の、座標平面をつかった練習が足りていない。
また、グラフの読み取り問題前の、グラフを描く練習が足りていない。
こうした練習不足のために、生徒は「わからない」となってしまいます。
「そもそも座標ってなに?」
「三角形の面積を求める問題がむずかしい」
「 \(y=2x\) って比例の式がなんで直線になるの?」
「反比例の式がグラフから読み取れない」
こういう例はすべて、上記2つに起因しているんです。
[比例反比例の記事一覧]
そこでこの記事では、上記2つの原因を解消するような指導方法・指導順を、ポイントをしぼって解説します。
座標の教え方について、基本・応用・発展と計9段階。
比例のグラフの教え方について、5段階。
反比例のグラフの教え方について、3段階。
最後に実践編として、3段階。
ここで紹介する指導案をぜひ参考にして、比例・反比例の「座標とグラフ問題」を解決してあげてください。
座標の指導案(基本)
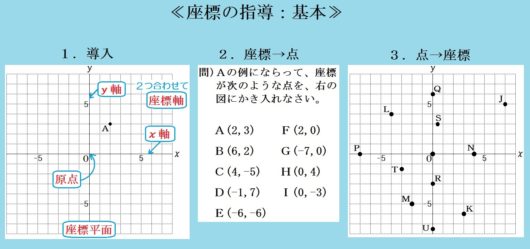
まずは座標の導入と基本問題からです。
ここの3項目は生徒の能力やつまずきに関係なく、全員に指導すべき内容になります。
なお、読みやすさを優先したいので、各項目の内容は「押さえるべきポイント」と「指導上のコツ」のみをかんたんに列挙していきます。
このブログの読者の方は、要点さえつかめばあとは自分でやるって人が多いと思うので(くわしい指導例はYouTubeなどにあるし)。
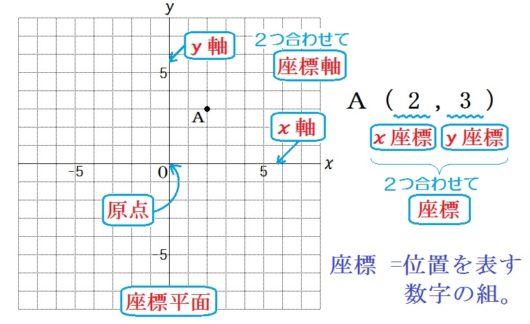
1.導入
【ポイント】
座標とは、位置を表す数の組。
【指導上のコツ】
○まず小6の比例・反比例の復習から入り、つぎに負の数も追加していくとスムーズ。
○各用語の説明は、言葉でなく、図に書き入れたほうが理解が早い(現代の子どもたちは言語情報より視覚情報の処理に優れているから)。
○A(2,3) の読み方は「に さん」「に カンマ さん」「に の さん」「に と さん」、どれでもいい(決まっていない)。学校での教え方に倣うこと。
負の数の追加
2.座標→点をかき入れる問題
【ポイント】
\(x\) 座標がよこ、\(y\) 座標がたての目盛り。
【指導上のコツ】
○あらかじめ、よくやるミスとして、\(x\) 座標と \(y\) 座標を逆にしてしまう例を示すこと。生徒の注意をうながせる。
○F(2,0) は、させてみて、正解したらほめるといい。
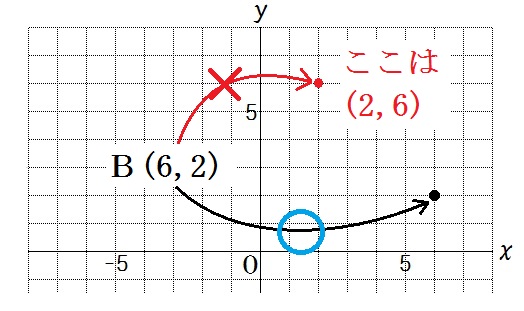
よくやるミス
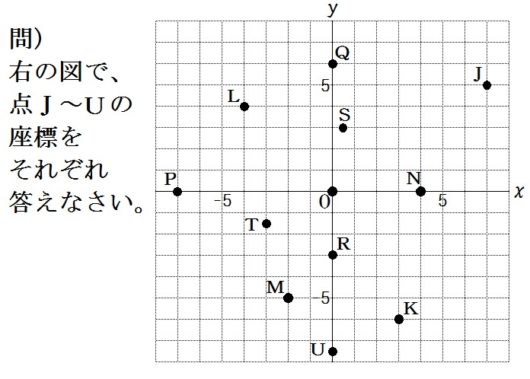
3.点→座標を読みとる問題
【ポイント】
\(x\) 座標がよこ、\(y\) 座標がたての目盛り。
【指導上のコツ】
○やはりあらかじめ、よくやるミスとして、\(x\) 座標と \(y\) 座標を逆にしてしまう例を示すこと。生徒の注意をうながせる。
○「,」を「.」と書く生徒がけっこういる。小数点とまちがえてしまうのでこれはバツになる。生徒の回答をよくみて、手元指導すること。
○S( \( \frac{1}{2}\) ,3 )、T(-3, \( \frac{3}{2}\) )、U(0, \( -\frac{15}{2}\) )のような点も問題に出すこと。すべての実数が座標平面上に表せるという意識につながる(もちろんむずかしい生徒にはアドバイスしてよい。また小数表記でもよい)。
座標の指導案(応用)
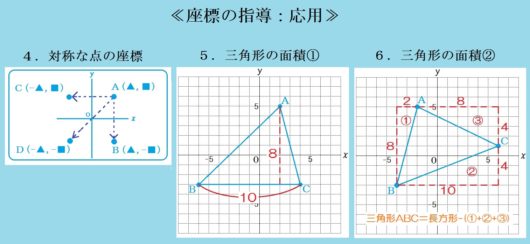
つぎに座標の応用問題です。
ここの3項目も、できればすべての生徒に教えてほしい。
ジュウゴの経験上、たとえ定期テストで30点台の中学生でも、簡潔にわかりやすく教えればできるようになります。
それ以上の生徒であれば、もちろん指導してください。
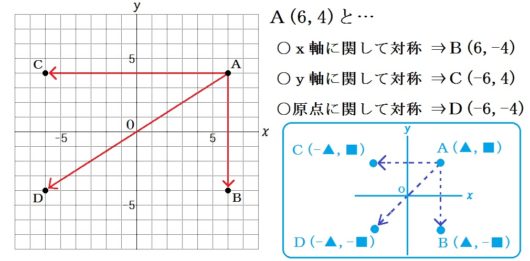
4.対称な点の座標
【ポイント】
対称な点の座標は符号だけ変わる。
【指導上のコツ】
○むずかしい日本語は訳してあげること。つまり
- 「x軸に関して対称」=x軸で折りまげる
- 「y軸に関して対称」=y軸で折りまげる
- 「原点に関して対称」=原点をとおって同じ長さだけ向こう側
など。なお、教科書や参考書によっては「x軸について対称」という言葉使いもあるが、おなじ意味。
○実際に出題される問題としては、たとえばこんなの↓
答.B(-3,-5)、C(3,5)、D(3,-5)
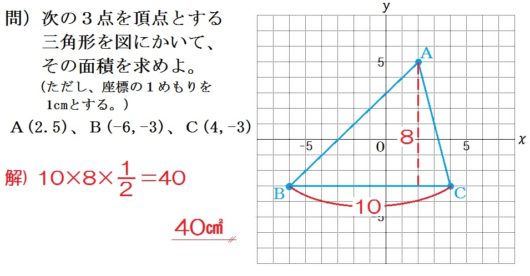
5.座標平面上の三角形の面積①
【ポイント】
$$ \mbox{三角形の面積}= \mbox{(底辺)} \times \mbox{(高さ)} \times \frac{1}{2}$$
【指導上のコツ】
○座標平面上に長さをかきこむこと。このコツが身についていれば、模試や入試で役に立つ。
○最初はめもりを数えて長さを計ってもいいが、慣れてきたら計算で出せることも示すこと。
$$ \mbox{底辺:} 4-(-6)=10 $$
$$ \mbox{高さ:} 5-(-3)=8 $$
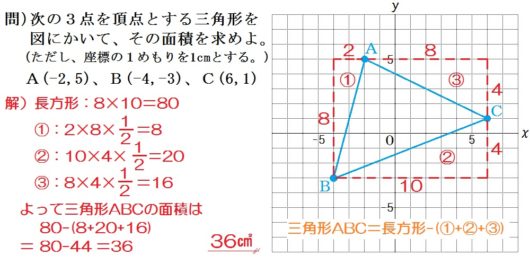
6.座標平面上の三角形の面積②
【ポイント】
複雑な図形の面積を求めるには
- 分けて、たす
- 大きく求めて、いらない部分をひく
という2通りの方法がある。今回は2.でいける。
【指導上のコツ】
○やはり、座標平面上に長さをかきこむこと。このコツが中3時に入試でおおいに役に立つ。
○面積を求める式を、整理して書かせること(余白に書きなぐらない)。そうじゃないと、「いま何をやっているか」がわからなくなるときがあるから。ややこしい問題ではすべてそう。
座標の指導案(発展)
基本、応用ときて、つづいては座標の発展問題です。
ここの3項目は、定期テストで平均未満の中学生にはさせなくてもかまいません。
逆にいえば、偏差値50以上の高校をねらうなら学習させるべき内容となります。
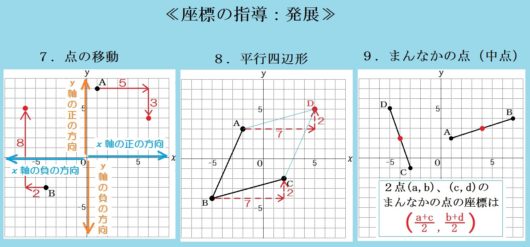
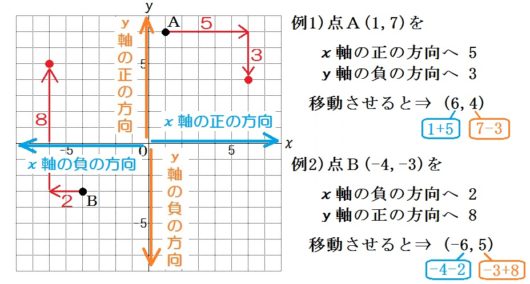
7.点の移動
【ポイント】
よこに何マス、たてに何マスと移動させるだけ。
【指導上のコツ】
○むずかしい日本語は訳してあげること。つまり
- 「x軸の正の方向」=右
- 「x軸の負の方向」=左
- 「y軸の正の方向」=上
- 「y軸の負の方向」=下
○慣れてきたら、座標平面がなくとも計算で座標を出せるように指導していくこと。「つまりこんな計算をしてる」と、\(1+5\) や \(7-3\) などを示せばいい。
○実際に出題される問題としては、たとえばこんなの↓
問)2点A(3,5)、B(-4,6) がある。次の□にあてはまる語句や数を答えなさい。
点Aをx軸の□の方向へ□、y軸の□の方向へ□だけ移動すると、点Bに重なる。
答.順に「負」「7」「正」「1」
8.平行四辺形
【ポイント】
①出来上がりの図をイメージして、
②おなじだけ点を移動させる。
【指導上のコツ】
○「点の移動」を学習してからこの平行四辺形の問題に入ること。
○むずかしい生徒には、図にあるような矢印をかかせるとよい。
○平行四辺形の性質については中2「三角形と四角形」単元でくわしく学習するので、ここでは深く立ち入らなくてもよい。
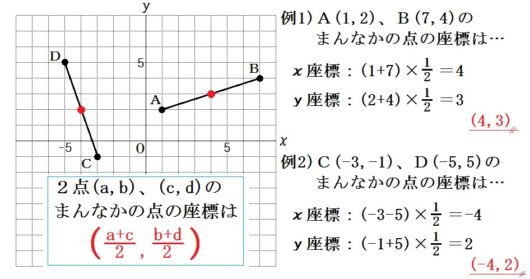
9.まんなかの点(中点)
【ポイント】
2点P(\(a\) , \(b\))、Q(\(c\) , \(d\)) のまんなかの座標は
$$ \left( \frac{a+c}{2} , \frac{b+d}{2} \right) $$
【指導上のコツ】
○「つまり、それぞれ足して半分」と、わかりやすくかみくだいて説明すること。
○「中点」という言葉はこのあとの中1「平面図形」単元で習うが、予習として先に教えてもいい。
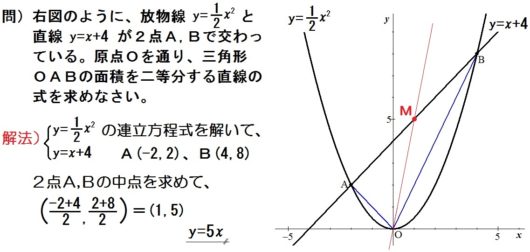
○まんなかの点(中点)がパッと出せるようになると、高校入試頻出の「座標平面上の三角形の面積を二等分する問題」が解きやすくなる↓
以上、座標について計9段階の指導項目と、それぞれの指導方法でした。
グラフに入る前にこれだけ練習すれば、座標平面を図形的に扱うことに慣れるでしょう。
つづいて、比例のグラフと反比例のグラフの指導に入ります。
[比例反比例の記事一覧]







コメント
ここまでの指導の流れで、
①関数とは?→変数・定数・変域
②比例・反比例の式 主に式の形に注目し、「xが○のとき、yが□である」ときの式を求める。
③座標
からの今回の記事だと思うのですが、ここに至るまで表の特徴に一切触れておらず、今回も式からグラフをかくための仲介役(ゆくゆくは仲介せずにしますが)としての役割しかないのですが、それは良いのでしょうか?
具体的には、
比例…変化(xを○倍するとyも○倍)と対応(y÷x=比例定数に一定、x≠0)
反比例…変化(xを○倍すると、yは1/○倍)と対応(x×y=比例定数に一定)
といったことを表から読み取らせなくてもよいかということです。
三角形の面積を求める問題②(x軸、y軸に平行な辺がないバージョン)、
定期テスト30点の生徒でもできるようになる、
とはすごいですね。
自分の経験からすると、
定期テスト70,80点の生徒でもなかなか厳しいです。
「指導上のコツ」、参考になりました。