中学数学「比例と反比例」の教え方⑤ 座標とグラフ

座標につづき、「比例のグラフ」と「反比例のグラフ」の指導順・指導項目です。

比例のグラフについて、5段階。

反比例のグラフについて、3段階。

そしてグラフの実践編として、3段階。

それぞれポイントと指導上のコツを記すので、教師や講師、また保護者の方は数学指導の参考にしてください。

＞前ページ「座標平面の導入」

比例のグラフ
反比例のグラフ
比例・反比例のグラフ実践編
まとめ

比例のグラフ

まず比例のグラフの教え方です。

ここでは「グラフをかく」ことを４段階にわけて十分に練習し、それから「グラフの読み取り」にすすむことが肝要になります。

１．表をつくってグラフを描く

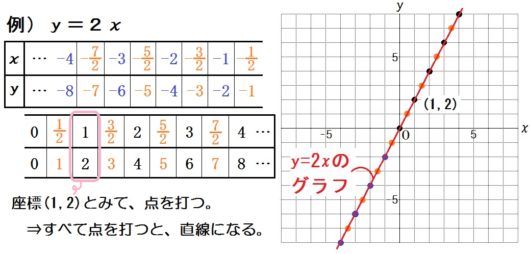
表をつくって比例のグラフを描く

【ポイント】

比例のグラフは直線になる。

【指導上のコツ】

○まず表をつくるとき、$x$ の値を式に「代入」して $y$ を出す、ということを復習する。
→参考：比例の式を求める

○つぎに、$x$ と $y$ の値の組を座標とみなして点を打つ、と示す。

○黒→青→オレンジの順で点を打っていく。大切なのは「点が集まって直線になる」イメージ。

○「もちろん $ \left( \frac{1}{10} , \frac{1}{5} \right) $ のように、細かすぎて打ちきれない点もこの直線上にある」等も示すこと。

○あと２～３例、表をつくってグラフを描かせるとよい。たとえば以下のグラフ。

$$ y=-2x \quad y=\frac{1}{2}x $$

２．表なしでグラフを描く

表なしで比例のグラフを描く

【ポイント】

$ (x,y)$ の整数の組を頭のなかで計算して、その座標の点を打つ。

【指導上のコツ】

○暗算力の劣る生徒には、ひとつひとつ手元指導すること。たとえば↓

「$x=0$ のときの $y$ は？」
「$0$」
「じゃ $(0,0)$ に点を打って」

○問２が、（比例定数が）分数の場合のやり方だと伝える。

○あと４～５例、点を打つことでグラフを描かせるとよい。たとえば以下のグラフ。

$$ y=\frac{2}{3}x \quad y=\frac{3}{4}x $$

$$ y=-\frac{1}{4}x \quad y=-\frac{5}{2}x $$

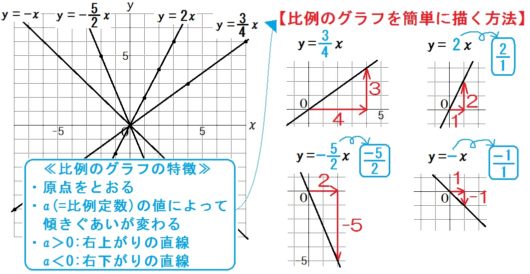
３．かんたんにグラフを描く方法

比例のグラフをかんたんに描く方法

【ポイント】

$$ y=\frac{\mbox{▲}}{\mbox{●}}x \quad \mbox{のグラフは}$$

原点スタートで、
右に●、上に▲ の直線

【指導上のコツ】

○以下の指導順を守ること。（生徒に「わかりにくい」と言われる教師はこの順番がメチャクチャだったりする。）

点を打つことでさまざまなグラフを描く
比例のグラフの特徴を帰納する
かんたんな描き方があると示す

○比例定数が整数の場合もあえて分数に直すこと。また、マイナスは分子につけること。

○「左に●」とまちがえる生徒がよくいる。「まず右。次に上か下」と強調すること。

○２点だけとって直線をひくと、端のほうでズレる場合も多い。「右に4行って、上に3。右に4行って、上に3…」等と、マス目の最後まで点を取らせること。また左側へも「4もどったら、下に3。4もどったら、下に3…」等と、やはり最後まで点をかきこむように指導する。

くもんの中学基礎がため100％中1数学（関数・図形編）改訂新版学習指導要領対応

posted with カエレバ

楽天市場

Amazon

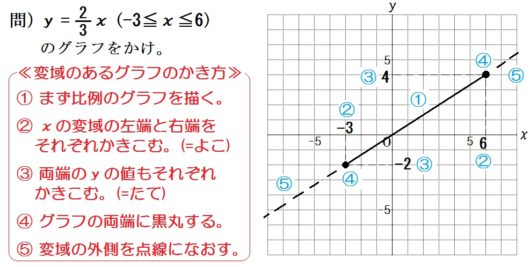
４．変域のあるグラフ

変域のあるグラフ問題

【ポイント】

以下の手順どおりにやるだけ。

まずグラフを描く
$x$ の変域の両端をかきこむ（＝よこ）
$y$ の値もそれぞれかきこむ（＝たて）
グラフの両端に黒丸する
変域の外側を点線になおす

【指導上のコツ】

○グラフの変域問題は中２、中３でも難しがる生徒が多いが、ここで示した手順どおりにやればクリアしていける。

○ $x$ に対応する $y$ の値を出すとき、「比例の式に代入して計算」でも出せると示すこと。この一指導をくわえることで、マス目なしのグラフ問題でも解けるようになる。

$$ y=\frac{2}{3} \times (-3) = -2 $$

$$ y=\frac{2}{3} \times 6 = 4 $$

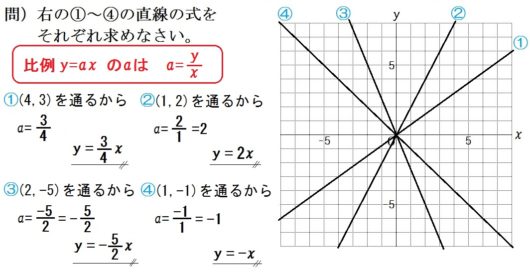
５．グラフ→式の読み取り問題

グラフから比例の式を読み取る問題

【ポイント】

直線が点 (●,▲) を通るなら、比例定数 $a$ は

$$ a= \frac{\mbox{▲}}{\mbox{●}}$$

【指導上のコツ】

○比例の比例定数の求め方は $a=\frac{y}{x}$
→比例の式を求める

○マス目のちょうどいい点（ｘ座標とｙ座標がともに整数の点）を見つけることさえできれば、むずかしくない。

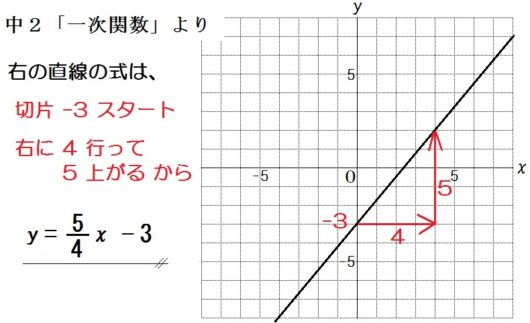
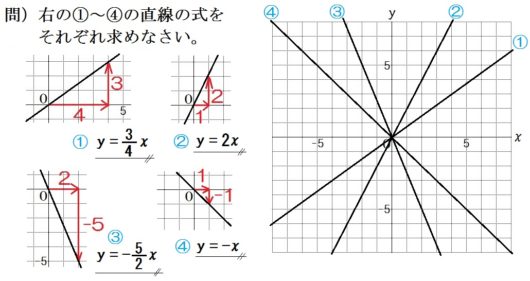
○なお、「３．かんたんにグラフを描く方法」の逆をつかって、式を求めることもできる↓

グラフから比例の式を読み取るもうひとつの方法

この２通りの方法、どちらも生徒に教えること。
前者の方法は、マス目なしの応用問題につながる。
後者の方法は、中２「一次関数」につながるから↓

中学数学発展篇方程式と関数改訂新版

posted with カエレバ

楽天市場

Amazon

反比例のグラフ

つぎに反比例のグラフの教え方です。

ここでも比例と同様、「グラフをかく」ことに習熟してから「グラフの読み取り」にすすむことが肝心です。

１．表をつくってグラフを描く

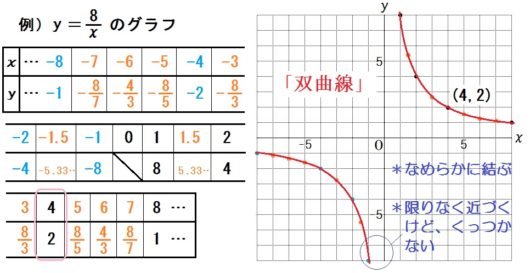
表をつくって反比例のグラフを描く

【ポイント】

反比例のグラフは双曲線になる。

【指導上のコツ】

○指導の流れは比例のときとほぼ同じ。ちがうのは以下３点。

$x=0$ のとき $y$ の値はなし。なぜなら $0$ で割れないから。
なめらかな曲線で結ぶこと。折れ線みたいになる生徒が多いので注意。
座標軸にグラフをくっつけてしまう生徒も多いので注意。「かぎりなく近づくけど、くっつかない」と伝える。（漸近線という言葉は高校で習う）

２．表なしでグラフを描く

表なしで反比例のグラフを描く

【ポイント】

$ (x,y)$ の整数の組を頭のなかで計算して、その座標の点を打つ。

【指導上のコツ】

○暗算力の劣る生徒にはやはり、ひとつひとつ指導すること。たとえば↓

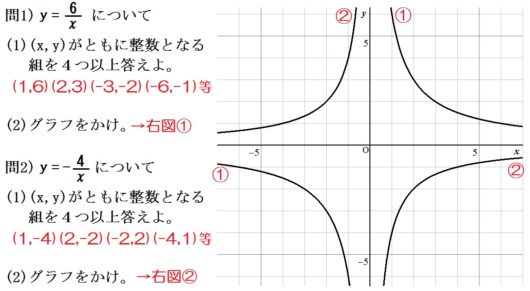
「$x=1$ のときの $y$ は？」
「$6$」
「じゃ $(1,6)$ に点を打って」

○あと３～４例、反比例のグラフを描かせた後、反比例の式の特徴も伝えること。つまり「原点に関して対称である」と。

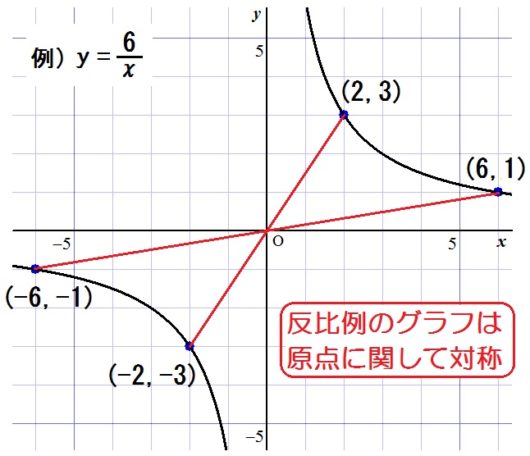
反比例のグラフは原点に関して対称

３．グラフ→式の読み取り問題

グラフから反比例の式を求める問題

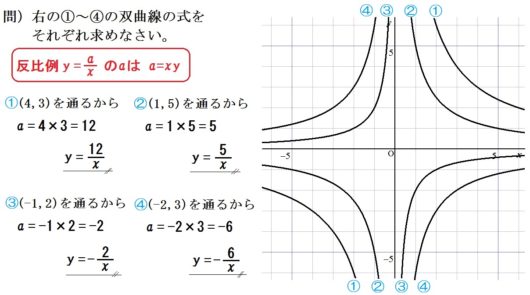
【ポイント】

双曲線が点 (●,▲) を通るなら、比例定数 $a$ は

$$ a= \mbox{●} \times \mbox{▲} $$

【指導上のコツ】

○反比例の比例定数の求め方は $a=xy$
→反比例の式を求める

○マス目のちょうどいい点（ｘ座標とｙ座標がともに整数の点）を見つけることさえできれば、むずかしくない。

中1数学の比例と反比例定期テストに自信がもてる！（これでだいじょうぶ！シリーズ）

posted with カエレバ

楽天市場

Amazon

比例・反比例のグラフ実践編

さいごに、比例・反比例のグラフの実践問題です。

定期テストや模試などでよく出る問題、３種類の、それぞれのポイントを伝えます。

なお、ここから座標平面のマス目がなくなります。

たとえマス目がなくても、最低１点さえあればグラフの式が読み取れることを、最初に生徒には伝えてください。

１．座標から式を求める問題

座標から式を求める問題

【ポイント】

直線 ⇔ 比例 $y=ax$ ⇔ $a=\frac{y}{x}$

双曲線 ⇔ 反比例 $y=\frac{a}{x}$ ⇔ $a=xy$

【解答】

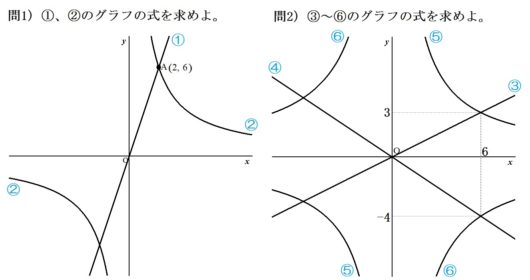
①直線がＡ(2,6)を通るから、

$$ a=\frac{6}{2}=3 \quad \mbox{答．}y=3x $$

②双曲線がＡ(2,6)を通るから、

$$ a= 2 \times 6 =12 \quad \mbox{答．}y=\frac{12}{x} $$

③直線が(6,3)を通るから、

$$ a=\frac{3}{6}=\frac{1}{2} \quad \mbox{答．}y=\frac{1}{2}x $$

④直線が(6,-4)を通るから、

$$ a=\frac{-4}{6}=- \frac{2}{3} \quad \mbox{答．}y=- \frac{2}{3}x $$

⑤双曲線が(6,3)を通るから、

$$ a= 6 \times 3 =18 \quad \mbox{答．}y=\frac{18}{x} $$

⑥双曲線が(6,-4)を通るから、

$$ a= 6 \times (-4) =-24 \quad \mbox{答．}y=- \frac{24}{x} $$

2019年受験用全国高校入試問題正解数学 [ 旺文社 ]

posted with カエレバ

楽天市場

Amazon

２．式から座標も求める問題

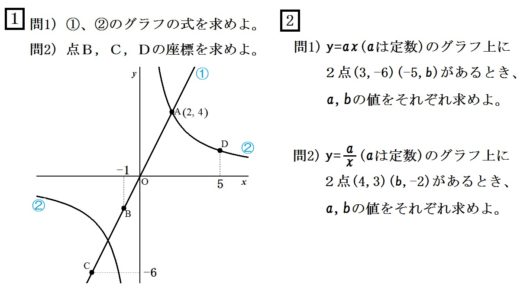
式からさらに座標も求める問題

【ポイント】

$ (x,y)$ のうち、片方がわかっててもう片方を求めるときは「代入」。

【解答１】

①直線がＡ(2,4)を通るから、

$$ a=\frac{4}{2}=2 \quad \mbox{答．}y=2x $$

②双曲線がＡ(2,4)を通るから、

$$ a= 2 \times 4 =8 \quad \mbox{答．}y=\frac{8}{x} $$

Ｂ．$y=2x$ に $x=-1$ を代入して、

\begin{eqnarray} y &=& 2 \times (-1) \\ y &=& -2 \qquad \mbox{答．}B(-1,-2) \end{eqnarray}

Ｃ．$y=2x$ に $y=-6$ を代入して、

\begin{eqnarray} -6 &=& 2x \\ 2x &=& -6 \\ x &=& -3 \qquad \mbox{答．}C(-3,-6) \end{eqnarray}

Ｄ．$y=\frac{8}{x}$ に $x=5$ を代入して、

$$ y = \frac{8}{5} \qquad \mbox{答．}D(5,\frac{8}{5}) $$

【解答２】

問１）$a=\frac{-6}{3}=-2$ よって、$y=-2x$

$y=-2x$ に $x=-5$ 、$y=b$ を代入して、

\begin{eqnarray} b &=& -2 \times (-5) \\ b &=& 10 \qquad \mbox{答．}a=-2 , b=10 \end{eqnarray}

問２）$a=4 \times 3 =12$ よって、$y=\frac{12}{x}$

$y=\frac{12}{x}$ に $x=b$ 、$y=-2$ を代入して、

\begin{eqnarray} -2 &=& \frac{12}{b} \\ -2b &=& 12 \\ b &=& -6 \qquad \mbox{答．}a=12 , b=-6 \end{eqnarray}

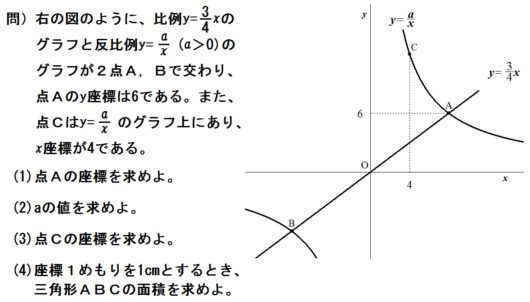
３．グラフと三角形の面積

比例と反比例のグラフ：まとめ問題

【ポイント】

いままでの知識をフル活用。

【解答】

(1) $y=\frac{3}{4}x$ に $y=6$ を代入して、

\begin{eqnarray} 6 &=& \frac{3}{4}x \\ \frac{3}{4}x &=& 6 \\ x &=& 8 \qquad \mbox{答．}A(8,6) \end{eqnarray}

(2) 双曲線がA(8,6) を通るから、

$$ a= 8 \times 6 = 48 $$

(3) $y=\frac{48}{x}$ に $x=4$ を代入して、

\begin{eqnarray} y &=& \frac{48}{4} \\ y &=& 12 \qquad \mbox{答．}C(4,12) \end{eqnarray}

(4) 点Ｂは、点Ａと原点に関して対称なので、$ B(-8,-6) $

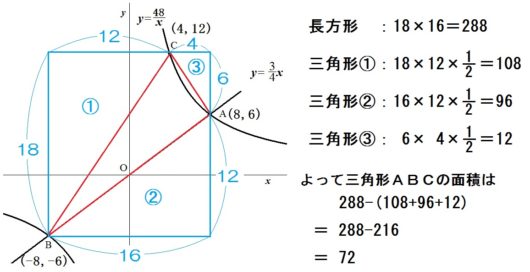
答．７２㎠

この問題は「比例と反比例」③および「比例と反比例」④で挙げた応用問題です。

最高水準問題集数学中学1年（シグマベスト） [ 文英堂 ]

posted with カエレバ

楽天市場

Amazon

まとめ

おつかれさまでした。

中１数学「比例と反比例」における座標・グラフの教え方、まとめます。

○座標・グラフでつまずく原因は２つ。

座標平面を図形的に扱うことに慣れていない
「グラフは点の集まり」という意識が育ってない

○そこで、座標平面をつかった練習を、以下９段階で行う。
（リンクをクリックすると各項目が開きます）

○また、比例のグラフを以下５段階にわけて教える。
（リンクをクリックすると各項目が開きます）

○反比例のグラフも同様に、３段階にわけて教える。
（リンクをクリックすると各項目が開きます）

○こうした順番をふめば、以下３種類の応用問題もできるようになる。
（リンクをクリックすると各項目が開きます）

次回は「比例と反比例」の最後、文章問題です。

比例か反比例かを見分けるコツ。

そして文章問題すべてに当てはまる解き方を伝えます。

→中学数学「比例と反比例」⑥　文章問題のコツ(基本・応用)

[比例反比例の記事一覧]