中1数学「比例と反比例」の教え方2回目。
前回は「関数とは何か」について、教える側がもつべき知識と視点について述べました。
プロローグはおしまい。
今回からいよいよ実際の指導方法を解説していきます。
[比例反比例の記事一覧]
- 中1「比例と反比例」① 関数とは何か
- 中1「比例と反比例」② 導入と用語
- 中1「比例と反比例」③ 比例の式を求める
- 中1「比例と反比例」④ 反比例の式を求める
- 中1「比例と反比例」⑤ 座標とグラフ
- 中1「比例と反比例」⑥ 文章問題(基本・応用)
- 中1「比例と反比例」⑦ 文章問題(図形・速さ・歯車)
[関連記事]
前回の記事で、比例・反比例の最初(関数の導入)でつまずく原因のひとつは、早すぎる抽象化だと述べました。いきなり \(x\) と \(y\) を使う、いきなり \(y=2x\) と関係式まで文字で表す、いきなり変数を定義する…。こうしたいきなりの抽象化、そして具体例の乏しさが中学生の頭を「?」にしているのだと。
そこでここでは、
- 関数とは何か?
- 変数・定数・変域はどういう意味か?
この2点について、具体から徐々に抽象化していく指導例を提示します。
とくに数学が苦手な中学生。
また、納得しなければ先にすすまない性格の子にたいして、有効な指導法になります。
中1をお持ちの保護者の方、講師や中学教師の方、どうぞ参考にしてください。
「関数の導入」指導例

以下では関数の導入における指導例を示します。
教科書の記述や、多くの中学校における指導計画とちがう点は主に2つ。
- はじめから \(x\) と \(y\) という文字を使わない。関係式も最初は日本語で示す
- 具体例を3,4つ示してから抽象化する
ほかにも異なる点はありますが、そうした工夫は後述の「指導上の注意点」でくわしく書きます。
まずは実際の指導方法をご覧ください。
導入の最初:関数とは何か
(数学の4分野を紹介したあとに)
関数とは何か?
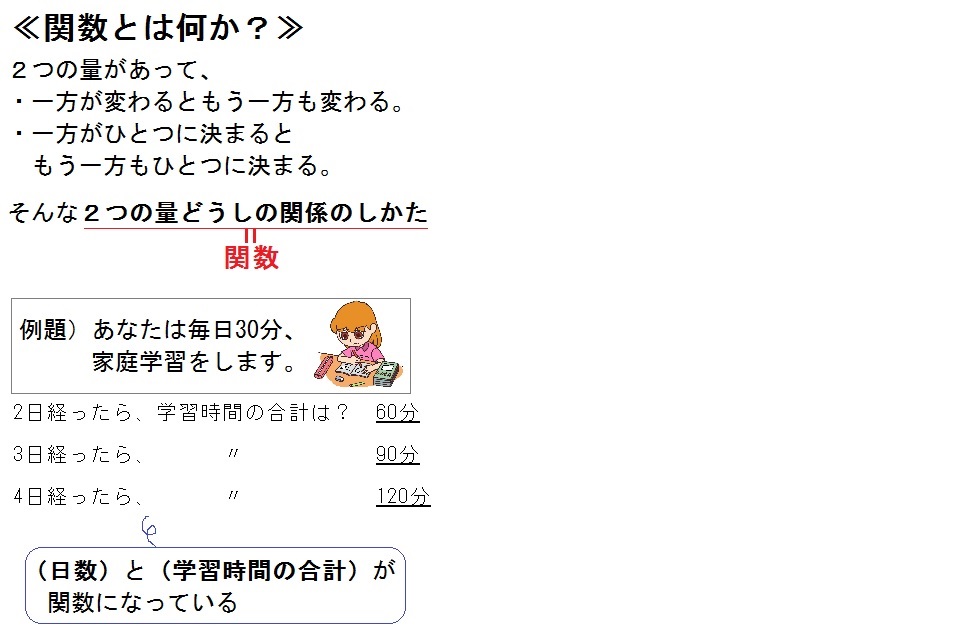
2つの量があって、一方が変わるともう一方も変わる。
一方がひとつに決まるともう一方もひとつに決まる。
そんな2つの量どうしの関係のしかたを見ていこうという分野。
この「2つの量どうしの関係のしかた」=関数という。
たとえば…
2日経ったら、学習時間の合計は?→60分
3日経ったら、学習時間の合計は?→90分
4日経ったら、学習時間の合計は?→120分
……
このとき、(日数)と(学習時間の合計)という2つの量が関数になってる。
じゃあ、
365日経ったら、学習時間の合計は?
→ \(30 \times 365 =10950 \) で10950分。
1000日経ったら、学習時間の合計は?
→ \(30 \times 1000 = 30000 \) で3万分。
このように、何日経ったとしても、学習時間の合計は \(30 \times \mbox{(日数)} \) で求められる。
つまり
$$ \mbox{(学習時間の合計)} = 30 \times \mbox{(日数)} $$
だから、
(日数)と(学習時間の合計)の関係のしかたは?と聞かれたら、たったひとつの式を示せばいい。
$$ \mbox{(学習時間の合計)} = 30 \times \mbox{(日数)} $$
です、と。
このような関係を表す式を答えたり。
また、この式を使って「365日経ったときの学習時間の合計は?」という問題に答えたり。
そして2つの量の関係をグラフに描いたり。
こういうのが、関数という分野でやること。
抽象化する前に:具体例の提示
では、ちょっと練習しよう。
まずは関係を表す式を答えることから。
以下の問題に答えなさい。
問1)30L入る水槽に、毎分2Lの割合で水を入れていく。このとき、(時間)と(水の量)との関係をみていこう。
①3分後の水の量は何L?
②11分後の水の量は何L?
③次の表をぜんぶうめなさい。
④(時間(分))と(水の量(L))の関係を表す式を完成させなさい。
問2)1000gのでっかいプリンを、何人かの子どもに等しく分けていく。このとき、(子どもの人数)と(1人当たりのプリンの量)との関係をみていこう。
①2人に分けたら、1人当たり何g?
②40人に分けたら、1人当たり何g?
③次の表をぜんぶうめなさい。
④(子どもの人数(人))と(1人当たりのプリンの量(g))の関係を表す式を完成させなさい。
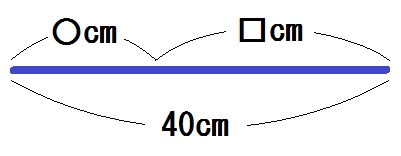
問3)40cmのひもから○cm切り取った残りを□cmとする。
①関係する量は何と何か?
②○=15のとき、□の値は?
③次の表をぜんぶうめなさい。
④○と□の関係を表す式を完成させなさい。
具体から抽象へ:文字を使う
ここまで2つの量を日本語や○□で書いてきた。
けど、かっこわるいので、これからは \(x\) と \(y\) を使う。
問1の(時間)と(水の量)の代わりに \(x\) と \(y\) を使うと、式は
$$ y=2x $$
問2の(子どもの人数)と(1人当たりのプリンの量)の代わりに \(x\) と \(y\) を使うと、式は
$$ y= \frac{1000}{x}$$
問3の○と□の代わりに \(x\) と \(y\) を使うと、式は
$$ y= 40-x $$
これから関係を表す式、つまり関数の式といえばこの \(x\) と \(y\) を使った等式ということにする。
さて、3つの式を見比べて、何か共通点はない?
そう、かならず \(y=\) の形になってるね。
ほかにも、右辺にはかならず \(x\) が入っている。
じつはこれは数学の世界における暗黙の了解で、関数の式はかならずこういう形で書くことになっている。
つまり、\(y\) を \(x\) の式で表した形。
今後「 \(y\) を \(x\) の式で表せ」という問題が出てきたら、「 \(y= \mbox{(xを使った式)}\) 」という形で関数の式を答えよってことです。
まとめと演習
ここまでの内容をまとめます。
2つの量 \(x\) と \(y\) があって、\(x\) が変われば \(y\) も変わる、\(x\) がひとつに決まれば \(y\) の値もひとつに決まる。このとき、\(x\) と \(y\) の対応関係を関数という。
関数は \(y= \mbox{(xを使った式)} \) という等式で表される。
また「 \(y\) は \(x\) の関数である」ともいう。
$$ y=30x \qquad y=2x $$
$$ y= \frac{1000}{x} \qquad y= 40-x $$
じゃあ演習問題に取り組もう。
「次のうち、\(y\) が \(x\) の関数であるものはどれか」という問題。
注意すべきは、2つの量どうしが関係しないものは関数じゃない。
たとえば身長と体重とかね。
演習:次のうち、\(y\) が \(x\) の関数であるものはどれか。
ア. プールに毎分5Lの割合で水を入れたときの \(x\) 分後の水の量 \(y\) L
イ. 100個のあめ玉を \(x\) 人で分けたときの1人当たりの個数 \(y\) 個
ウ. 身長 \(x\) cmの人の体重 \(y\) kg
エ. 4000円持って買い物に行き、\(x\) 円の商品を買ったときの残金 \(y\) 円
オ. 1辺が \(x\) cmの正方形の面積 \(y\) ㎠
カ. 1日の最低気温 \(x\) ℃と最高気温 \(y\) ℃
解答:ア、イ、エ、オ
指導上の注意点
以上が関数の導入の指導例です。
ここでの注意点は4つ。
1.はじめの例はなじみやすいものに
関数の導入でよく使われる例はこんなの。
- (ガソリン)と(走行距離)
- (時間)と(道のり)
- 長方形における(縦の長さ)と(面積)
中学生にとっては、まーなじみにくい。
せっかく「具体例から関数を導入する」のだから、もっと中学生自身が身にひきつけて考えられる例にすべきです。
ジュウゴの経験からいえば、中学生にとってなじみぶかい三大例は勉強・部活・お金。
だから指導例のように「1日○分勉強する」とか。
「1日○回の素振りをする」とか。
「1か月につき500円ずつ貯金していく」とか。
中学生にとってよりイメージしやすい例から始めましょう。

2.具体例は2つ以上
人は新しい概念を定義するとき、かならず2つ以上の具体例から帰納します。
幼児がたくさんワンちゃんを見てはじめて「犬」を定義するように。
小学生がいろんな大きさの□に出あってはじめて「正方形」を定義するように。
だから「関数」を定義するときも、例は1つでなく、2つ以上挙げるべき。
たとえ数学が演繹的な手法の学問だとしても、人間は経験の生き物です。
とくに導入部分の指導ではそれを忘れずに。
3.いきなり \(x\) と \(y\) を使わない
これは公立中学で平均点以下を取る生徒にだけ当てはまります。
よって私立の生徒や、公立でもつねに数学テストの平均点+10点以上を取る中学生には、いきなり \(x\) と \(y\) で導入してもいいでしょう。
それ以外の生徒、つまり日本の中学生の約半分は、いきなり \(x\) と \(y\) を使われると大なり小なり混乱をきたします。
なぜなら文字の使用にじゅうぶん慣れていないから。
つまり文字による代用が一般化・抽象化であるとまだ理解していないから。
なので、日本語から導入したほうがわかりやすくなります。
4.ブラックボックスのたとえはもっと後
「関数とは何か」を説明するとき、なぜか日本の数学教育ではブラックボックスのたとえがよく使われます。
自動販売機とか、ふしぎ箱とかのあれですね。
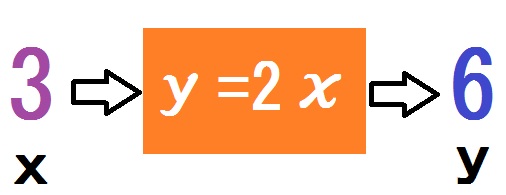
ブラックボックスのたとえ
これは関数の本質をよく表しているたとえなんですが、導入には不向きです。
だって、あくまで「たとえ」だから。
数学としての定義を、具体例からすこしずつ発展させてまっすぐに教えて、そのあとに初めて使うべきです。
「たとえるなら、自動販売機みたいなもん」って。
なので、ブラックボックスのたとえは「比例・反比例をすでに習ったけどよくわからない」という中学生向けの余談として話すべきでしょう。
「用語の説明」指導例

さて、ここまでが関数の導入です。
ここからは関数で使う用語を定義していきます。
つまり「変数」「定数」「変域」が何を意味するのか?
ここでもやはり、具体例からすこしずつ抽象化することで、わかりやすい指導を心がけましょう。
以下、実際の指導例をどうぞ。
変数と定数
次に、関数で出てくる3つの言葉を説明します。
(上図の黒板のような定義を書く)。
ひとつひとつ説明していくね。
まず「変数」「定数」だけど、ここで \(x\) と \(y\) を使って、もういちど例題と問題1を一緒にやってみよう。
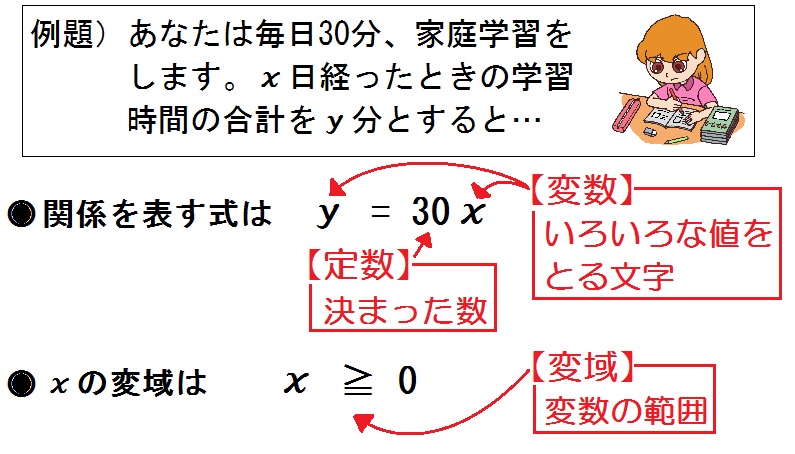
例題)あなたは毎日30分、家庭学習をします。\(x\) 日経ったときの学習時間の合計を \(y\) 分とすると…
①次の表をぜんぶうめよ。
② \(y\) を \(x\) の式で表せ。
$$ y=30x $$
問1)30L入る水槽に、毎分2Lの割合で水を入れていく。このとき、\(x\) 分後の水の量を \(y\) Lとすると…
①次の表をぜんぶうめよ。
② \(y\) を \(x\) の式で表せ。
$$ y=2x $$
よくできた!
さて、例題の \(y=30x\) という式を見て。
この式の \(x\) と \(y\) にはいろんな数が入るよね。
\begin{eqnarray} 0&=&30 \times 0 \\ 30&=&30 \times 1 \\ 60&=&30 \times 2 \\ 90&=&30 \times 3 \\ 120&=&30 \times 4 \\ 300&=&30 \times 10 \\ \ldots \end{eqnarray}
また、問1の \(y=2x\) という式。
ここの \(x\) と \(y\) にもいろいろな数が入るよね。
\begin{eqnarray} 0&=&2 \times 0 \\ 2&=&2 \times 1 \\ 4&=&2 \times 2 \\ 6&=&2 \times 3 \\ 8&=&2 \times 4 \\ 28&=&2 \times 14 \\ 30&=&2 \times 15 \end{eqnarray}
もちろん問2の \(y= \frac{1000}{x}\) の \(x\) と \(y\) にも、問3の \(y=40-x\) の \(x\) と \(y\) にも、いろんな数が入る。
つまり、関係を表す式(=関数の式)の \(x\) と \(y\) には、いろいろな数(=値)が入る。
言い方をかえれば、この2つの文字に入れる値はいろいろに変えていい。
だから、関係を表す式で、\(x\) と \(y\) のことを「変数」という。
変数… \(y=30x\) の \(x\) と \(y\) のように、いろいろな値をとる文字
いっぽう、\(y=30x\) という式のなかで、 \(30\) という数字は変わらない。
\(y=2x\) の \(2\) も、定まったままだ。
このように、関係を表す式(=関数の式)のなかでずっと同じ、決まったままで変わらない数字を「定数」という。
定数… \(y=30x\) の \(30\) のように、決まった数
ようするに、\(y= \mbox{数字} \times x\) という関数の式があったら、
\(x\) と \(y\) は変数
数字は定数
ってこと。
変域
いま、変数 \(x\) と \(y\) はいろいろな値をとると言った。
しかし、問題によっては、値に制限がある場合もある。
たとえば例題の \(x\) 。
例題)あなたは毎日30分、家庭学習をします。\(x\) 日経ったときの学習時間の合計を \(y\) 分とすると…
ここの \(x\) に、\(-5\) を入れてもいい?
ダメだね。
だって \(-5\) 日後、つまり5日前とか、この問題じゃ考えてないもんね。
だからこの例題においては、変数 \(x\) に範囲がある。
いちばん小さくて?そう、\(0\) だ。
いちばん大きくて?うん、大きいほうには制限はない。
つまり、この例題における変数 \(x\) の範囲は
\(0\) 以上
このような変数の範囲のことを「変域」という。
変域…変数の範囲
そして変域は不等号で表す。
だから例題における \(x\) の変域は
\(x\) ≧ \(0\) または \(0\) ≦ \(x\)
不等号を忘れた人は、↓見て思い出してね。

じゃ、問題1にも変域があるんで、一緒に考えてみよう。
問1)30L入る水槽に、毎分2Lの割合で水を入れていく。このとき、\(x\) 分後の水の量を \(y\) Lとすると…
変数 \(x\) のとる値は、いちばん小さくて?
そう、\(0\) だね。
じゃ、いちばん大きくて?
そう、\(15\) だね。15分で水槽いっぱいになるから。
よって、変数 \(x\) の変域は?と聞かれたら、
\(0\) ≦ \(x\) ≦ \(15\)
このように、問題文から変域を答えるときには、「いちばん小さくて(最小)」と「いちばん大きくて(最大)」を考えるといい。
そして不等号を使って書くこと。最小と最大がどっちもあるときは、\(x\) をまんなかに置いて書くこと。
ちなみに、\(15\) ≧ \(x\) ≧ \(0\) と書いてもいい。
ただ小さい順に書くことのほうが数学の世界では多いよ。
え、\(y\) の変域はやらないのかって?
やってみてごらん。
例題では、\(y\) ≧ \(0\) 。
問1では、\(0\) ≦ \(y\) ≦ \(30\) 。
よくできた。
まとめと演習
以上、「変数」「定数」「変域」という3つの用語を理解した。
ここまでの内容をまとめます。
じゃ、最後に演習問題をやってみよう。
ひとこぎ(ペダル1回転)で \(5\) m進む自転車で、400mのトラックを一周する。\(x\) 回こいだときの自転車の進む距離を \(y\) mとすると…
①関係を表す式を答えよ( \(y\) を \(x\) の式で表せ)。
②①の式で変数と定数はそれぞれどれか、答えよ。
③ \(y\) の変域を求めよ。
④ \(x\) の変域を求めよ。
解)① \(y=5x\) ②変数:\(x\) と \(y\) 定数:\(5\) ③ \(0\) ≦ \(y\) ≦ \(400\) ④ \(0\) ≦ \(x\) ≦ \(80\)
指導上の注意点
ここまでが用語の説明の指導例です。
ここでの注意点は、2つ。
1.具体例は2つ以上
関数の導入のときとおなじです。
何かの概念を定義するときにはかならず具体例を2つ以上挙げること。
現行の中学教育では、具体例が少なすぎる。
「これも変数、こっちも変数」と言ってはじめて、子どもは概念を獲得していきます。
ここの指導を省かないように。
2.新しい概念を導入するときの基本手順
「具体例は2つ以上」とも関連しますが、中学生に何か新しい概念を教えるとき、ジュウゴが気をつけている基本というものがあります。
それは以下の手順をふむこと。
- まずかんたんな説明を示す
- 具体例を2つ以上挙げてイメージさせる
- つまりこういうこと、とまとめる
- ようするにこうだと、わかりやすく極論する
- アウトプットさせて定着度を確認する
たとえば変数・定数の説明ではこの5段階がよくわかると思います。
この5段階の手順を守ることで、ほとんどの生徒が納得していきます。
導入部分の指導が苦手という教師・講師の方はぜひ参考にしてください。
>Amazonプライム・ビデオで「じゃりン子チエ 劇場版」を観る
まとめ

関数の導入において気をつける点は以下3つ。
- はじめから \(x\) と \(y\) という文字を使わない。とくに平均点以下の生徒には、関係式も日本語で示してから文字につなげる。
- 具体例を2つ以上示してから、徐々に帰納していく。これが概念獲得のコツ。
- 最初の具体例は勉強・部活・お金など、中学1年生にとって身近なものに。ガソリンと走行距離などは導入例として不適。

また、関数の導入にかぎらず、新しい概念を導入するときには以下5つの手順をふんで。
- まずかんたんな説明を示す
- 具体例を2つ以上挙げてイメージさせる
- つまりこういうこと、とまとめる
- ようするにこうだと、わかりやすく極論する
- アウトプットさせて定着度を確認する

以上、「比例と反比例」における関数の導入指導例でした。
次回から比例・反比例の式を求める問題に入ります。
[比例反比例の記事一覧]






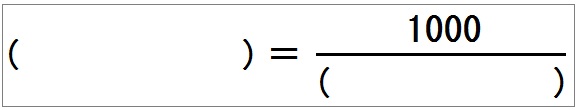









コメント
定数という用語についてですが、例えば紐を切り取る問題をx、yで表すとy=40-xの定数はなんですか?とい聞かれたらどう答えますか?
基本的にこれは一次関数の形であり、2年生での習得内容ですが40と-1というように説明しますか?
導入の5つのポイントはたいへん参考になりました。
「関数とは何か?」については、
具体例はもちろんですが、
反例(身長と体重とか)を説明すると、たいていの生徒は納得してくれると感じています。
上の例では、演習のときにさらっと触れられていますが、
私は先に説明するようにしています。
なお、「一方が変わるともう一方も変わる」「x が変われば y も変わる」は無い方が良いかと思います。
「一方がひとつに決まるともう一方もひとつに決まる」「xがひとつに決まるとyもひとつに決まる」で十分かと。
それとも、あえて、定数関数を除外したのでしょうか?
あえて、しています。
「一方が変わるともう一方も変わる」という文は教科書の定義にはありませんが、これを付け加えることで、関数とは2変数のあいだの関係を扱うんだと強調したいからです。