前回につづいて、「比例と反比例」の文章問題をやっつけます。
今回は
- 図形、動点の問題
- 速さ、圧力の問題
- 歯車、てんびんの問題
の3パターン。
つまり「公式にあてはめて関係式をつくる」問題です。
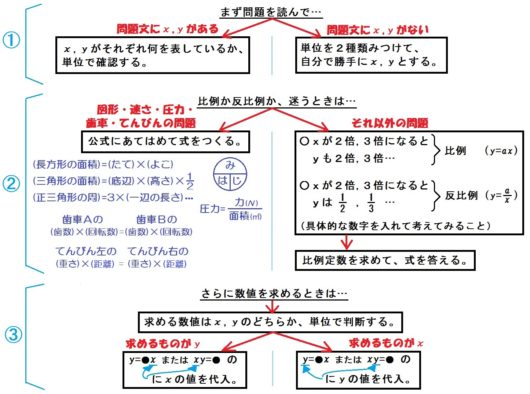
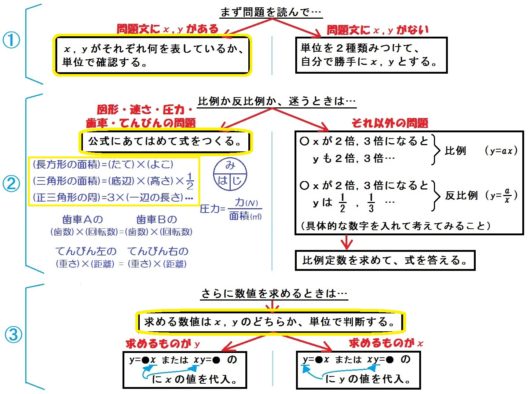
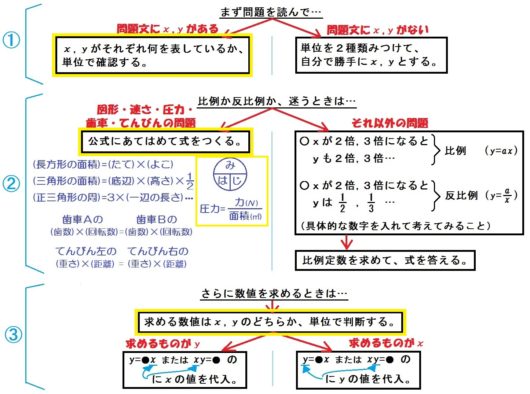
前回同様、フローチャートに沿ってやっていけばぜんぶ解けます。
前回の記事:中学数学「比例と反比例」⑥文章問題のコツ(基本・応用)
くわえてここでは、それぞれの問題のコツをお伝えします。
この記事を読み終われば、比例・反比例の文章問題はすべてマスターとなるでしょう。
ではどうぞ。
図形・動点の問題
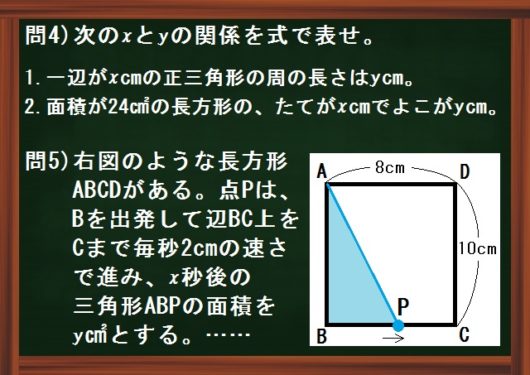
このような図形・動点の問題は、公式にあてはめて関係式をつくるだけです。
「いや、そう言われても、イメージできない」。
こういう生徒には、1次方程式 文章題 図形の記事で紹介した2つのコツを使うといいでしょう。
- 図がなかったら自分できれいに描く
- 文字もつかって長さをぜんぶ書きこむ
「よし、イメージはできた、でも式がつくれない」。
こういう生徒には、文字と式 数量の表し方の記事等で紹介したコツを使いましょう。
- 具体的な数字におきかえて考える
- 何算するかを意識する
ということで、これら合計4つのコツを使えば、どんなに図形が苦手な中学生でも関係式をみちびくことができます。
以下、実際に解いてみましょう。
スポンサーリンク
図形の基本問題(正三角形)
問4)次の \(x\) と \(y\) の関係を式で表せ。
1.一辺が \(x\) cmの正三角形の周の長さは \(y\) cm。
まずは問4の1.から。
フローチャートどおり、問題文を読んで、文中に \(x\) と \(y\) があることを確認します。
どちらも単位はcmですが、
- \(x\) は1辺の長さ
- \(y\) は周ぜんぶあわせた長さ
です。
つぎに関係式を立てていきますが、ここで「わからない、イメージできない」という場合は、図を描いて長さも書きこみます。
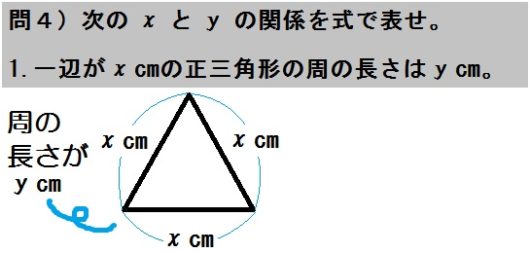
こんなふうに描けたら、もうわかる人にはわかる。
しかし、ここまできて「式が立てられない」という中学生は、\(x\) を具体的な数字におきかえて \(y\) を出してみましょう。
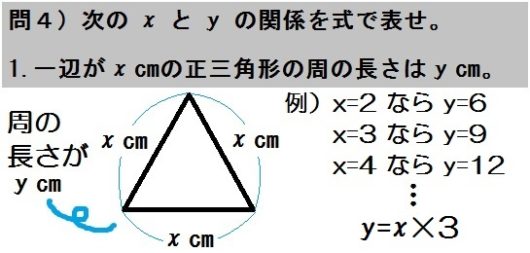
このとき、\(y\) を求めるのに何算したか、つねに意識すること。
だから、とうぜん「かけ算」とわかります。
よって答えは、
$$ \mbox{答.} y=3x $$
図形の基本問題(長方形)
問4)次の \(x\) と \(y\) の関係を式で表せ。
2.面積が \(24\) ㎠の長方形の、たてが \(x\) cmでよこが \(y\) cm。
つづけて問4の2.も解きましょう。
やはり問題文に \(x\) と \(y\) があり、\(x\) はたて、\(y\) はよこの長さです。
つぎに関係式を答えますが、イメージしづらい場合は図をきれいに描いて長さも書きこみましょう。
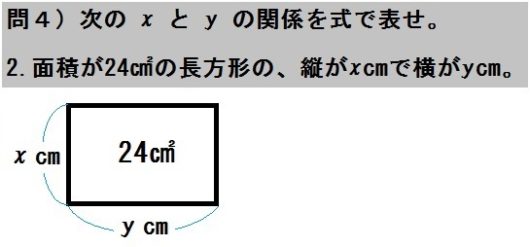
この段階でわかる人は、式を出せばいい。
しかしわからない人は、\(x\) を具体的な数字におきかえて \(y\) を出してみる。
そしてその際に何算したか、つねに意識する。
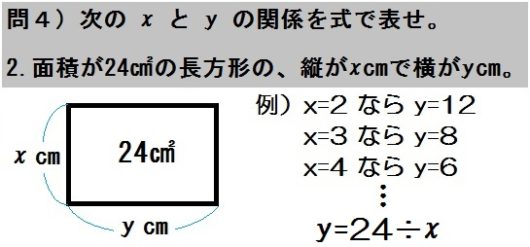
より、\(y\) を出すには「わり算」とわかります。
よって答えは、
$$ \mbox{答.} y=\frac{24}{x} $$
このように、図形問題では、公式にあてはめるとともに、
- イメージしにくい場合、図をきれいに描いて長さも書きこむこと。
- 式を立てられない場合、\(x\) を具体的な数字でおきかえて \(y\) を求め、何算したか意識すること。
これがコツになります。
動点(点が移動する)問題
問5)右図のような長方形ABCDがある。点Pは、Bを出発して辺BC上をCまで毎秒 \(2\) cmの速さで進み、\(x\) 秒後の三角形ABPの面積を \(y\) ㎠とする。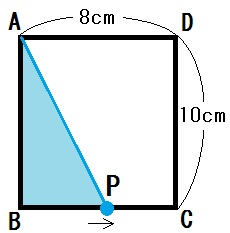
- \(x\) と \(y\) の関係を式で表せ。
- \(x\) の変域を求めよ。
- 三角形ABPの面積が \(35\) ㎠となるのは、点PがBを出発してから何秒後か。
図形のさいごは点が移動する問題、つまり動点の問題です。
1次方程式 文章題 図形を読んだ方はもう知ってますね、
動点問題のコツは、上記2つのコツに加えて、
- 点の通った長さを \(x\) で表すこと
だと。
1.\(x\) と \(y\) の関係を式で表せ。
\(x\) は点Pが出発してからの秒数、\(y\) は三角形ABPの面積。
…と確認したら、あとはコツをつかって公式にあてはめていきます。
この問5はすでにきれいな図があるので、あとは長さを書きこみます。
そして問5において点Pが通った長さは、BPにあたります。
Pは毎秒 \(2\) cmの速さで進むので、BPを \(x\) で表すと…
そう、\(2x\) cmですね。
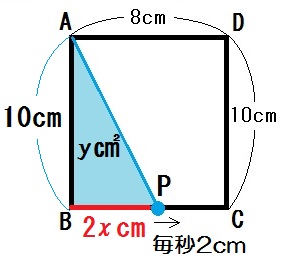
より、
\begin{eqnarray} y &=& 2x \times 10 \times \frac{1}{2} \\ y &=& 10x \end{eqnarray}
答.\(y=10x\) と出ます。
なお、「いきなり式は立てられない」という中学生は、\(x\) を具体的な数字におきかえて \(y\) を求めてみましょう。
2.\(x\) の変域を求めよ。
つぎに変域について。
「比例と反比例」②の記事でも書きましたが、変域とはようするに範囲のこと。
んで、問題文から変域を答えるときには「いちばん小さくてなんぼ(最小)」と「いちばん大きくてなんぼ(最大)」を考えればいいんでした。
いま、\(x\) ってのは点PがBを出発してからCにたどりつくまでの時間(秒)です。
いちばん小さくてなんぼ?
→ \(0\) 秒ですね。
いちばん大きくてなんぼ?
→ \(4\) 秒ですね。\(4\) 秒後にCにたどりついちゃうから。
よって答えは
\(0\) ≦ \(x\) ≦ \(4\)
むずかしくないですね。
3.△ABPが \(35\) ㎠となるのは何秒後?
おしまいに、さらに数値を求めます。
久々、フローチャートにご登場ねがうと、以下の部分になります。
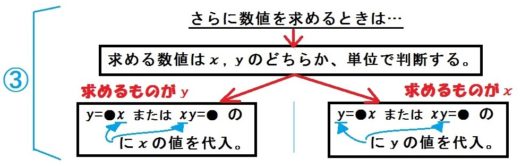
これ、前回の応用問題でもやりましたね。
わかってる方を関係式に代入してもう片方を求めるんでした。
いまわかってる \(35\) ㎠は、単位より、\(y\) のほう。
そして求める「何秒後」ってのは、\(x\) のほう。
よって、
\(y=10x\) に \(y=35\) を代入して、
\begin{eqnarray} 35 &=& 10x \\ 10x &=& 35 \\ x &=& \frac{7}{2} \end{eqnarray}
これは \(0\) ≦ \(x\) ≦ \(4\) を満たす。
答.\( \frac{7}{2} \) 秒後(3.5秒後)
なお、「これは \(0\) ≦ \(x\) ≦ \(4\) を満たす。」という一文。
中学生のうちは見過ごされることもありますが、高校数学の記述テストではこの一文が無いと減点対象になります。
なので、学力に余裕のある生徒はいまのうちから書くクセをつけておきましょう。
以上、「比例と反比例」文章問題における図形・動点問題でした。
まとめると、
- フローチャートに沿ってやるだけ
これに加えて、
- イメージしにくい場合、図をきれいに描いて長さも書きこむ
- とくに動点問題では、点の通った長さを \(x\) で表す
- それでも式が立たない場合、\(x\) を具体的な数字でおきかえて \(y\) を求め、何算したか意識する
というのがコツです。
速さ・圧力の問題

2パターン目は、速さ・圧力の問題です。
ここはまったくむずかしくありません。
公式さえおぼえたら、あとはあてはめるだけです。
速さ・時間・道のりの問題
問6)次の \(x\) と \(y\) の関係を式で表せ。
- 時速 \(x\) kmで \(6\) 時間走ると \(y\) kmすすむ。
- \(400\) mの道のりを分速 \(x\) mで歩くと \(y\) 分かかる。
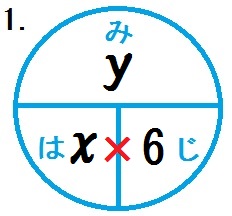
図より、1.の答え \(y=6x\)
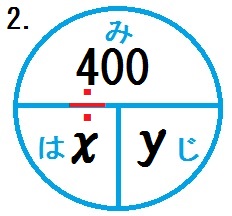
図より、2.の答え \(y= \frac{400}{x}\)
以上!
…
以下、ついで。
「そりゃやり方はわかるんだけど、自分でやろうとすると速さ問題がどうも苦手」。
こういう生徒はそもそも、速さとは何かの理解があやふやです。
また、「単位変換の問題がでたら、できない」。
こんな生徒もいます。
これらの中学生向けに、以下の記事ですでに解決方法を提示しています↓
参考にしてください。
圧力の問題
比例と反比例の文章題では、たまにこうした圧力の問題も出ます。
しかしこれも、圧力の公式さえおぼえたら、かんたんです。
圧力の公式はコレ↓
$$ \mbox{圧力(N/㎡)}= \frac{ \mbox{力(N)}}{\mbox{面積(㎡)}} $$
覚え方は、ただ暗記するよりも、単位から圧力の意味をつかむといいでしょう。
「圧力とはN/㎡、つまり1㎡あたりどれくらいの力がかかっているか」だと。
ちなみに1㎡はだいたい畳半分の広さです。
理科の勉強はこれくらいにして、問7をやっつけます。
比例と反比例⑥ 応用問題のときと同様、3段階にわけて解くと、以下のとおりです。
【1】文中に \(x\) と \(y\) がないので、面積を \(x\) ㎡、圧力を \(y\) N/㎡ とする。
【2】圧力の公式より、 \(x\) と \(y\) の関係式は
$$ y= \frac{6300}{x} $$
【3】この関係式に \(x=7\) を代入して
\begin{eqnarray} y &=& \frac{6300}{7} \\ y &=& 900 \end{eqnarray}
答.900 N/㎡
ただこの問7は、ほかの解き方もあります。
べつに比例・反比例の文章問題だと思わずに、ただ公式にあてはめるだけでも解けるんで、
$$ \frac{6300}{7}= 900 $$
答.900 N/㎡
とやってもかまいません。
以上、速さ・圧力問題でした。
まとめると、
- フローチャートに沿ってやるだけ
これに加えて、
- 公式が覚えられない場合、「速さとは何か」「圧力とは何か」の意味をちゃんと理解すること
がコツです。
歯車・てんびんの問題
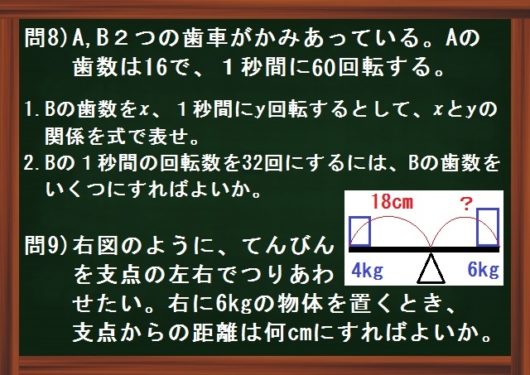
3パターン目は歯車とてんびんの問題です。
問8のような歯車の問題、また問9のようなてんびんの問題もやはり、公式にあてはめるだけです。
どんな公式かというと、コレ↓

歯車の問題
問8)A,B2つの歯車がかみあっている。Aの歯数は \(16\) で、1秒間に \(60\) 回転する。
- Bの歯数を \(x\) 、1秒間に \(y\) 回転するとして、 \(x\) と \(y\) の関係を式で表せ。
- Bの1秒間の回転数を \(32\) 回にするには、Bの歯数をいくつにすればよいか。
1.歯車の公式にあてはめて、
\begin{eqnarray} 16 \times 60 &=& xy \\ xy &=& 960 \\ y &=& \frac{960}{x} \end{eqnarray}
答.\(y = \frac{960}{x}\)
2.\(xy=960\) に \(y=32\) を代入して、
\begin{eqnarray} 32x &=& 960 \\ x &=& 30 \end{eqnarray}
答.Bの歯数30
以上!
…。
以下、むずかしいと感じる人に。
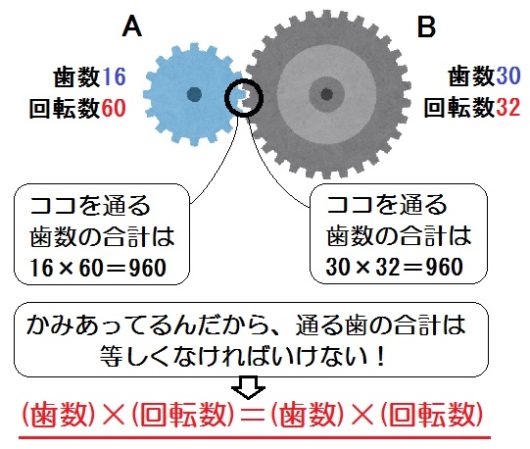
まず、なぜ歯車の公式が成り立つのか?
理由は、
- (歯数)×(回転数)=かみあってる部分を通る歯数の合計
- かみあってる部分を通る歯数の合計は、AとBで同じになる
からです。
こうした意味をしっかりつかむと、公式を忘れにくくなるでしょう。
また、1.の3行目の「両辺に \(\frac{1}{x}\) をかける」ことにとまどう場合。
こういう変形は中2「式と計算」の「等式の変形」で詳しくやりますが、ことばのまま変形すると以下のようになります。
\begin{eqnarray} \mbox{Aの歯数} \times \mbox{Aの回転数} &=& \mbox{Bの歯数} \times \mbox{Bの回転数} \\ \mbox{Bの歯数} \times \mbox{Bの回転数} &=& \mbox{Aの歯数} \times \mbox{Aの回転数} \\ \mbox{Bの回転数} &=& \frac{ \mbox{Aの歯数} \times \mbox{Aの回転数} }{ \mbox{Bの歯数} } \end{eqnarray}
こうした式変形ができないと、歯車およびてんびんの問題はむずかしい。
なんだこれ?慣れないなー、って中学生は、等式の性質を復習してください↓
てんびんの問題
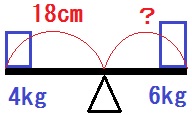
右に \(6\) kgの物体を置くとき、
支点からの距離は何cmにすればよいか。
さいごにてんびんの問題です。
この問9も先に解法を示します。
解き方は2通り。いずれもてんびんの公式を使います。
解法1は「比例と反比例」に沿った解き方。
解法2は「1次方程式」文章題の解き方です。

≪解法その1≫
【1】物体の重さを \(x\) kg、支点からの距離を \(y\) cmとする。
【2】てんびんの公式にあてはめて、
\begin{eqnarray} 4 \times 18 &=& xy \\ xy &=& 72 \end{eqnarray}
【3】\(xy=72\) に \(x=6\) を代入して、
\begin{eqnarray} 6y &=& 72 \\ y &=& 12 \end{eqnarray}
答.12cm
≪解法その2≫
支点からの距離を \(l\) cmとする。
てんびんの公式より、
\begin{eqnarray} 4 \times 18 &=& 6l \\ 6l &=& 72 \\ l &=& 12 \end{eqnarray}
答.12cm
さて、ここでもなぜてんびんの公式が成り立つのか?
深い話をすると高校物理に突入しちゃうので、かんたんに言うと、てこの原理と関係しています。
支点から近いほど、大きな力がいる。
支点から遠いほど、小さな力でいい。
こーゆーのがてこの原理でした。
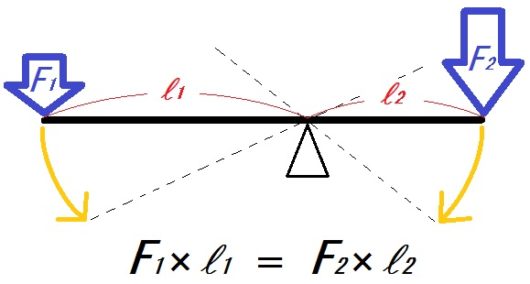
なので、てんびんの左右がつりあうためには、(支点からの距離)×(力の大きさ(重さ))が等しくなければいけない。
これがざっくりとした理由です。
(より詳しく知りたい人は「力のモーメント」「トルク」などで検索してください)
また、歯車の問題もそうでしたが、反比例の式からさらに数値を求めるとき、
「 \(xy=960\) に \(y=32\) を代入して」
「 \(xy=72\) に \(x=6\) を代入して」
としています。
これはなぜか、疑問に思う人はすでに過去記事で解説していますのでそちらを参照ください↓
とにかく、歯車問題・てんびん問題のコツは
≪歯車の公式≫
- (歯数)×(回転数)=(歯数)×(回転数)
≪てんびんの公式≫
- (距離)×(重さ)=(距離)×(重さ)
これを覚えて、はてはめるということです。
まとめ

以上、2回にわたって「比例と反比例」文章問題の解き方でした。
コツをまとめると、これだけです↓。
付け加えるなら、図形問題においては、
- イメージしにくい場合、図をきれいに描いて長さも書きこむ
- とくに動点問題では、点の通った長さを \(x\) で表す
- それでも式が立たない場合、\(x\) を具体的な数字でおきかえて \(y\) を求め、何算したか意識する
また、速さ・圧力・歯車・てんびん問題においては、
公式をおぼえるだけでなく、意味もちゃんと理解すると忘れにくい。
以上になります。
7回にわたった中1数学「比例と反比例」もこれで終わり。
次回からは「平面図形」に入ります。









コメント
今回もたいへん参考になりました。
こうしてみると、やはり、これまでに習った知識を使うことが多いですね。
単に、応用問題が解けない、で終わらせてはいけないな、と感じました。