中学数学の教え方について、具体的に解説するこの連載。
今回から中学１年生の３単元目「１次方程式」になります。
方程式とは何か、最初から教えてほしい…
解き方がわからない・つまずいている…
分数が混じるとできない、または計算ミスをする…
文章題のコツってないですか…
そんな生徒への指導に、ご参考ください。
[関連記事]
１回目はまず、１次方程式の導入です。
「１次方程式」単元に入ってすぐにわからない・できないという生徒。
このつまずきの原因は、おおきくわけると４つあります。
- それ以前の単元ですでにつまずいている
- 方程式とは何か、よくわかっていない
- 「\(x\) の係数を1にする」と「移項」の計算をごっちゃにしている
- 分数が出てくると思考停止する
これら４つの原因をとりのぞくためには、
- まず方程式とは何かをわかりやすく説明すること
- 次に、「\(x\) の係数を1にする」計算にまずじゅうぶん習熟すること
- そのなかで分数計算も同時に習熟し、それから「移項」に入ること
- そして、その時々で必要な復習をすること
以上の指導内容と指導順をおススメします。
では、具体的な教え方を見ていきましょう。
どんな症状がどの原因に当てはまるのか？
そしてそれぞれの解決法はどのようなものか？
順を追って説明します。
スポンサーリンク
方程式とは何か
まずはこの図のようなまちがいをする生徒。
こうした生徒は、方程式とは何かをよくわかっていない可能性があります。
そこで「方程式とは何か」「どのようにして解くのか」を、わかりやすく簡潔に説明してあげるといいでしょう。
[関連記事]中２連立方程式①
つまずく原因
方程式とは何かがわからない。
このような生徒は、方程式単元の最初の授業を聞き逃している場合があります。
その日に学校を休んでいたか、授業中に寝ていたか、ぼーっとしていたか。
あるいは、聞いていたけど理解できなかったのかもしれません。
いずれにしろ、最初の知識がぬけている。
そのために、方程式とは何かがわからなくなっているのです。
方程式単元の最初の知識は、このあと方程式をきりぬけていくために絶対に必要です。
とくに
- 「方程式」とは何か
- 「等式」とは何か
- 「方程式の解」とは何か
- 「方程式を解く」とはどういうことか
- 「等式の性質」
以上５個の知識は必ず身につけておかねばなりません。
よって、これら５個の知識をわかりやすく・簡潔に、生徒の頭に入れていくことが大切です。
実際の指導案を、以下、どうぞ。
指導案
①方程式とは「正体不明の『\(x\)』を含んだ等式」
方程式とは、正体不明の「\(x\)」を含んだ等式のこと。
等式とは、「＝」でつながった式のこと。
例えば、こんなの。
ちなみに「＝」の左側の式を「左辺」。
「＝」の右側の式を「右辺」。
左辺、右辺あわせて「両辺」という。
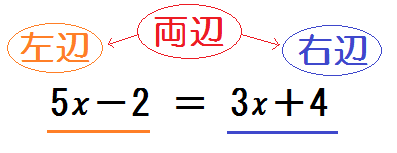
②方程式の解とは「\(x\) の正体」
この方程式を、どうにかして、「\(x =\)数字」の形に変える。
すると、\(x\) の正体がわかるわけ。
この\(x\) の正体、つまり「\(x =\)数字」を方程式の解という。
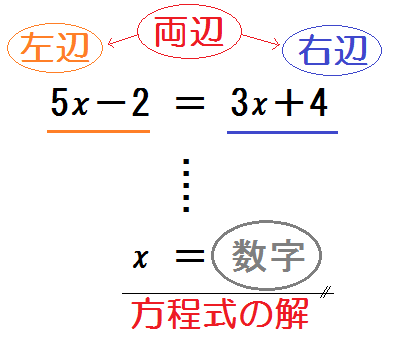
また、方程式を変形して「\(x =\)数字」の形にもっていくこと、つまり\(x\) の正体をハッキリさせることを、方程式を解くという。
ちなみにこの例題の方程式を解くと、解は「\(x = 3\)」。
③方程式を解く方法は？
では、どうやって方程式を解いたらいいのか？
当てずっぽうじゃなくて、必ず解ける方法はあるのか？
ある。
それは「等式の性質」を使った方法。
これを使えば、どんな方程式も解けるようになる。
だからちょっと寄り道して、「等式の性質」を５つ紹介する。
④「等式の性質」の紹介
例えば「\(1+3=4\)」という等式。
左辺は「\(1+3\)」で、右辺は「\(4\)」。
この両辺に \(2\) を足しても、やはり等しいままだ。
\begin{eqnarray} 1+3 &=& 4 \\ (1+3)+2 &=& 4+2 \\ 6 &=& 6 \end{eqnarray}
また、この両辺から \(2\) を引いても、やはり等しいままだ。
\begin{eqnarray} 1+3 &=& 4 \\ (1+3)-2 &=& 4-2 \\ 2 &=& 2 \end{eqnarray}
また、この両辺に \(2\) をかけても、やはり等しいままだ。
\begin{eqnarray} 1+3 &=& 4 \\ (1+3) \times 2 &=& 4 \times 2 \\ 8 &=& 8 \end{eqnarray}
また、この両辺を \(2\) で割っても、やはり等しいままだ。
\begin{eqnarray} 1+3 &=& 4 \\ \frac{1+3}{2} &=& \frac{4}{2} \\ 2 &=& 2 \end{eqnarray}
最後に、左辺と右辺を入れ替えても、やはり等しいままだ。
\begin{eqnarray} 1+3 &=& 4 \\ 4 &=& 1+3 \end{eqnarray}
以上５つのことを、文字を使って一般的に表すと、下のようになる。
⑤「等式の性質」を書き写す
当たり前のことみたいだけど、この「等式の性質」が、方程式を解くときに役立つ。
だから、ぜんぶ書き写して、しっかり理解して。
注意点
ここまでが、方程式の計算に入る前の導入です。
指導法は他にも多々ありますが、とにかく以下の５つの知識
- 「方程式」とは何か
- 「等式」とは何か
- 「方程式の解」とは何か
- 「方程式を解く」とはどういうことか
- 「等式の性質」
これらを身につけてから、実際の計算問題に入っていくことが肝心です。
そうでないと、生徒は方程式の計算をしながらも、「自分は今いったい何をやっているんだろう…」と自問することになります。
また、この指導案では「等式の性質」を例もあわせて書き写させます。
これは、方程式の解き方に慣れるためです。
つまりこの時点からすでに、以下のような解き方を自力で書けるようになるためのコーチングが始まっているのです。
\begin{eqnarray} 5x-2 &=& 3x+4 \\ 5x-3x &=& 4+2 \\ 2x &=& 6 \\ x &=& 3 \end{eqnarray}
よって、書き写させる際には、
- 「＝」を縦にそろえて書くこと
- 左辺の左に「＝」と書かないこと
この２点を注意するといいでしょう。
では次に、「\(x\) の係数を1にする」計算に入っていきます。
\(x\) の係数を1にする
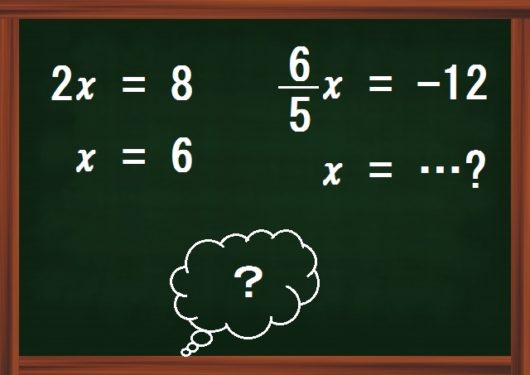
この図のように、初歩的な計算でミスをしたり、分数が混じると途端にできなくなる。
こんな生徒も、実際よくみかけます。
そして左の場合と右の場合では、原因がちがいます。
それぞれの原因を明らかにしてから、解決法をみていきましょう。
つまずく原因
\begin{eqnarray} 2x &=& 8 \\ x &=& 6 \end{eqnarray}
このようなミスは、「\(x\) の係数を1にする」計算と「移項」とをごっちゃにしているために起こります。
つまり、本当は両辺を\(2\)で割るべきなのに、両辺から\(2\)を引いてしまっているのです。
これは、学校教育の指導順にも一因があります。
というのも、学校では「等式の性質」を習ったすぐあとに、以下４つの計算をほぼ同時に習うからです。
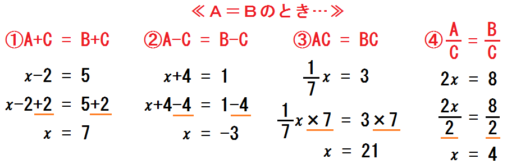
ほら、等式の性質を使えばいろんな方程式が解けるでしょ、と。
そのあと等式の性質①、②の応用として、「移項」を学習するのです。
これでは生徒が「\(x\) の係数を1にする」計算と「移項」とをごっちゃにするのもムリありません。
そこで、ここでは、まず「\(x\) の係数を1にする」計算だけを十分に習熟する方法をとります。
経験上、「\(x\) の係数を1にする」計算にしっかり習熟すれば、次の移項とごっちゃにすることはほぼないからです。
\begin{eqnarray} \frac{6}{5}x &=& -12 \\ x &=& \ldots \end{eqnarray}
また、分数が混じると思考停止してしまう場合。
これは、分数のかけ算が暗算でできないことに原因があります。
つまり、
$$ -12 \times \frac{5}{6} =-10 $$
この計算が頭の中でパッと瞬時にできないため、不安になり、脳と手が止まるのです。
よってこういう生徒はまず、分数のかけ算を、とくに(整数)×(分数)問題を復習するといいでしょう。
分数かけ算の暗算による復習方法は、以前の記事にくわしく書いていますので、参照ください。
記事内「分数まじりの分配法則：かけ算」の項です↓
また、そもそも分数のかけ算自体あまり自信がない、最大公約数でパッと約分できないという場合は、小６の分数かけ算・わり算を復習すべきです。
その復習方法もちがう記事で書いていますので、参照ください。
こちらは記事内「３つ以上の乗除計算でまちがえる」の「原因」の項です↓
これらの復習を済ませてから、または同時並行で進めながら、「\(x\) の係数を1にする」計算に入っていきます。
以下、指導案をどうぞ。
指導案
① 方程式の計算の導入
いよいよ方程式を解いていく。
たとえば \(3x=12\) のような方程式。
これを \(x=\)●(数字)の形にしたい。
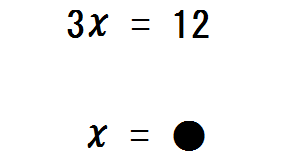
ちなみに \(x\) の前には \(1\) が隠れている。
この \(3\) を \(1\) にしたい。どうすればいいか？
そう、３で割ればいい。
つまり、\( \frac{1}{3}\) をかければいい。
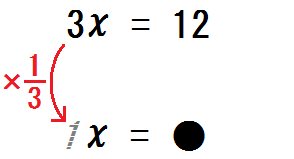
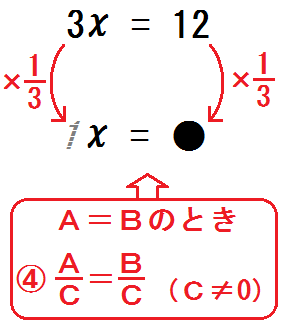
ここで、「等式の性質④」を使う。
両辺を同じ数で割っても等しいままだった。
だから、両辺に \( \times \frac{1}{3}\) をすればいいんだ！
左辺は、ただの \(x\) になった。
右辺は、\(12 \times \frac{1}{3}\) で？
そう、\(4\) 。
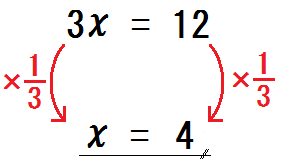
この方程式の解は、\(x=4\) と解けた。
②類題の練習と、分数の導入
同じようにして、以下の問題を解いてみよう。
（「両辺に何をかける？」「\(x=\) ？」と発問しながら、一緒に解く）
$$ 2x=8 \quad 6x=54 \quad 14x=42 $$
$$ 5x=-10 \quad 7x=-49 \quad 8x=-8 \ldots $$
さて、気づいたかな？
要するに、\(x\) の係数の逆数をかければいいんだ。
では、次の方程式を解いてみよう。
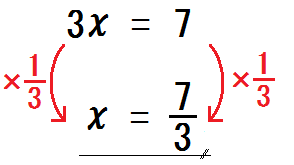
このように、解が分数になることもある。
ちなみに小数に直さなくてもいいからね。
じゃあ、つぎの方程式は？
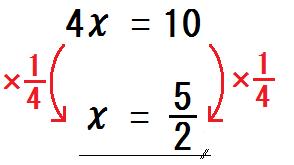
そう、約分できたら約分すること。
そして約分は暗算ですること。
以下、練習問題を解いてみよう。
$$ 6x=5 \quad 6x=15 \quad 10x=5 \quad 8x=20 $$
$$ 7x=-2 \quad 4x=-26 \quad 12x=-42 \quad 24x=-3 \ldots $$
③係数が分数
このように、\(x\) の係数を \(1\) にするには両辺に逆数をかければいい。
では、次の方程式を解くには、両辺に何をかければいいだろう。
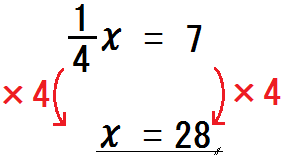
そう、\(4\) だね。
じゃ、この問題は？
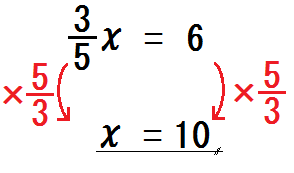
そう、\( \frac{5}{3}\) をかければいい。
ちなみにこれらの計算は、「等式の性質③」を使っている。
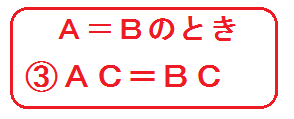
以下、分数まじりの問題も練習してみよう。
$$ \frac{1}{3}x=9 \quad \frac{2}{7}x=8 \quad \frac{16}{9}x=16 \quad \frac{15}{4}x=5 $$
$$ \frac{1}{2}x=-11 \quad \frac{6}{5}x=-12 \quad \frac{8}{3}x=-4 \quad \frac{7}{9}x=-9 \ldots $$
④係数に－がついた問題の練習
最後に、次の方程式は両辺に何をかければいい？
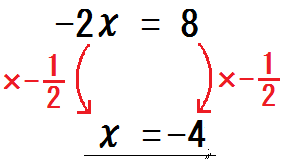
そう、「\(- \frac{1}{2}\)」だね。
では、次の方程式は？
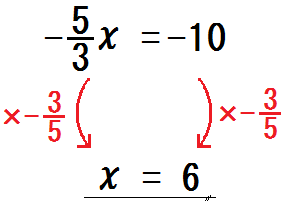
そう、「\(- \frac{3}{5}\)」だね。
以下の問題も練習してみよう。
$$ -7x=63 \quad -11x=-22 \quad -8x=-3 \quad -6x=20 $$
$$ -\frac{1}{5}x=1 \quad -\frac{4}{3}x=-7 \quad -\frac{2}{9}x=10 \quad -\frac{13}{6}x=-52 \ldots $$
⑤仕上げ
ここまでをまとめよう。
\(x\) の係数に何かついているときは、その係数の逆数を両辺にかけて「\(x=\)(数字)」の形にする。
それでは、たくさん練習して、「わかる」を「できる」にしていくこと。
注意点
ここまでが「\(x\) の係数を1にする」計算です。
見てわかるとおり、約分が暗算でできないとつらい。
たとえば、
\begin{eqnarray} -\frac{13}{6}x &=& -52 \\ x &=& 24 \end{eqnarray}
とできるためには、「\(13\) と \(52\)」が瞬時に「\(1\) と \(4\)」と約分できること。
そのうえで、\(4\) を頭の中で保持しながら「\(4 \times 6=24\)」とできることが必要です。
約分が暗算でできない生徒には、まず暗算できるように指導してから、ここに入りましょう。
また、符号「＋」「－」でミスを連発する場合、最初に符号を決めてから次に数字を計算させるといいでしょう。
「マイナス×プラスで、符号は？」「マイナス」
「\(x=-\) と書いて。次に数字の計算」
というように。
あと、各段階で練習問題を６～８問ほど書いていますが、この練習量は生徒の能力によって違えてください。
６～８問というのは、比較的計算力のある生徒用です。
それほど計算力のない中学生には、10～30問ていど練習させたほうがいいでしょう。
ただ残念ながら、どの問題集を見ても、この指導案ほどスモールステップで区切っているものがありません。
私（ジュウゴ）は毎年その場で自作していますが、いい無料プリントのサイトでもあれば教えてくださいm(_ _)m
なお、この指導案では「\(x\) の係数の逆数をかける」で統一しています。
先生によっては、\(2x=8\) などは「２で割る」。
\( \frac{6}{5}x=-12 \) などは「逆数をかける」、
と分けて教えていると思います。
というかむしろ、この教え方のほうが多い。
しかし、それによって分数に苦手意識をもったままの生徒がいることも事実です。
たとえば \(3x=7\) などの簡単な方程式も、「７を３で割れない！」と気づいた瞬間、思考停止してしまう。
こんな例が生まれてしまうのです。
分数にたいする苦手意識を克服させるためにも、「\(x\) の係数の逆数をかける」で統一して教えたほうがいいとジュウゴは考えます。
ちなみに逆数とは何かを忘れている生徒には、「かけて１になる数」だと復習してやってくださいね。
まとめ
長くなったので、とりあえずまとめます。
〇方程式とは何か、よくわからない生徒には…
- 方程式とは、正体不明の「\(x\)」を含んだ等式のこと。
- 等式とは、「＝」でつながった式のこと。
- \(x\) の正体、つまり「\(x=\)数字」を方程式の解という。
- 方程式を変形して「\(x=\)数字」の形にもっていくことを、方程式を解くという。
- 方程式を解くには、「等式の性質」５つを使っていく。
以上の事柄を、例を使ってわかりやすく伝える。
その際に、「＝」は縦にそろえて書くこと、また左辺の左に「＝」を書かないことを、例を使って体得させる。
〇最初の計算でミスをする、わからないという生徒には…
- まず「\(x\) の係数を1にする」計算に習熟すること。具体的には以下の手順。
- １．\(3x=12\) などの、解が整数のものから導入。
類題を練習したあと、係数の逆数を両辺にかければいいと伝える。 - ２．\(3x=7\) など、解が分数になる問題。約分は暗算ですると伝える。
- ３．\( \frac{3}{5}x=6\) など、係数が分数の問題。
- ４．係数に「－」がついた問題。
- ５．仕上げとして練習問題を解かせる。
約分が暗算でできない場合は、まず暗算でできるように復習してから。
当ブログでは「文字と式」単元であらかじめその練習をすることを推奨しています。
次回は「移項」、そして以下のような基本計算について解説します。
$$ 5x-2=3x+4 $$
「方程式の解き方がわからない」とつまずいている中学生に、いきなりこんな計算をさせちゃダメですからね。
今回の記事内容を実行してから、次回の内容に移ってください。
数学のつまずき解消のコツは、こまかく、スモールステップで。
コメント
[…] 式を娘に教える際にとても参考になりました。他の単元についても複数記事があるので悩んでいる場合にはおすすめです。 →参考：中１「１次方程式」でつまずく原因と解決法① 導入 […]
＞分数にたいする苦手意識を克服させるためにも、「x の係数の逆数をかける」で統一し＞て教えたほうがいいとジュウゴは考えます。
全くその通りだと思います。
そういう意味では、等式の性質④は教えない方が良い、とも思いますが、いかがでしょうか？
＞そういう意味では、等式の性質④は教えない方が良い、とも思いますが、いかがでしょうか？
いままで性質４を教えなかったことはないですね。
でも、試す価値はあるかもしれません。
来年度のことになりますが。
サンダー様も試されたのなら結果を教えてくださいm(_ _)m
回答ありがとうございます。
私は性質４は教えていません。
また、「ｘの係数の逆数を両辺に掛ける」で統一するようにしています。
しかし、学校で性質４や「ｘの係数で両辺を割る」を習っているせいか、生徒は割りたがります。
あまり効果は感じられていないのが現実です。