「1次方程式」の指導法解説、2回目。
今回は移項でつまずいている中学生、また以下のような1次方程式の基本計算がわからないという中学生への対処法です。
\begin{eqnarray} 5x-2 &=& 3x+4 \\ 5x-3x &=& 4+2 \\ 2x &=& 6 \\ x &=& 3 \end{eqnarray}
前回の最後にも書きましたが、「方程式の解き方がわからない」という中1に、いきなりこんな問題を解かせようとしてはいけません。
なぜなら、つまずきの原因になっている箇所よりも先の問題だから。
九九を習い始めた小学生に2ケタのわり算を教えるようなものです。
数学のつまずきを解消するには、順序よく、スモールステップが肝心。
よってまずは前回の内容から指導してください。
今回は、その続きになります。
[前の記事]中1「1次方程式」① 導入
[次の記事]中1「1次方程式」③ かっこ・小数
(数学指導法の記事一覧はまとめページへ)
移項
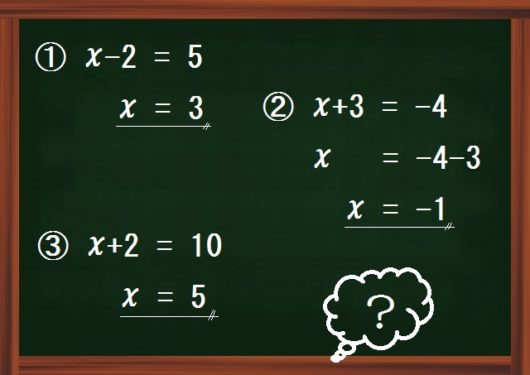
「移項」を習いはじめると、この図のような計算ミスをする生徒が出てきます。
①②③ではそれぞれ、ミスの原因が違います。
それぞれの原因を明らかにしてから、解決法を見ていきましょう。
つまずく原因
「移項」で計算ミスをする原因は、以下の3つです。
①途中式を書く習慣がない
②正負の加減に習熟していない
③「\(x\) の係数を1にする」計算とごっちゃ
①について。
\begin{eqnarray} x-2 &=& 5 \\ x &=& 3 \end{eqnarray}
このように、移項した後の式を書かずに、まちがえる。
これは、いまだ途中式を書く習慣のない生徒がよくやるミスです。
「中1の夏にもなって、まだそんな子がいるのか」と思うかもしれませんが、けっこういます。
ジュウゴの感覚では、中学1年生の段階で数学につまずく子が約3割。
そのうち半分くらいが「途中式を書く習慣がない」ためのつまづきです(あと半分は計算力不足)。
だから10人に1人くらいは、この方程式単元でも正しい途中式を書くことができません。
よって、移項を教えながら、同時に途中式を正しく書けるようにもする指導が必要です。
指導案では、そんな教え方の一例を紹介します。
ただ、どうしても途中式を書く習慣が身につかないという生徒には、復習もアリでしょう。
「正しい途中式を書かせる指導」については過去記事で触れていますので、ご参考ください↓

②について。
\begin{eqnarray} x+3 &=& -4 \\ x &=& -4-3 \\ x &=& -1 \end{eqnarray}
このように、移項した後の式はちゃんと書けるけど、その後の計算でまちがえる。
これは、正負の加減の計算に習熟していない生徒がよくやるミスです。
「中1の夏にもなって、まだそんな子が…」います!
10人に1人くらいはいます!でも見捨てない!
こういう生徒には、まず正負の加減をかんたんに復習したらいいでしょう。
方程式を解きながら同時並行で正負の加減も、というのはちょっと混乱をきたすので、短期集中でまず正負の加減を復習する。
それから当単元に戻ってくるというのをおススメします。
「正負の加減」の習熟方法について、学校とはちがうカンタンなやり方も、過去記事で紹介しています↓

③について。
\begin{eqnarray} x+2 &=& 10 \\ x &=& 5 \end{eqnarray}
このように、本当は \(-2\) と移項すべきところ、両辺に \(\times \frac{1}{2}\) をしてしまう。
これは、「\(x\) の係数を1にする」計算と「移項」とをごっちゃにしているミスです。
前回の記事で述べたように、学校の指導順だとこういう計算ミスもよく起こります。
しかし、当ブログではまず「\(x\) の係数を1にする」計算だけに十分習熟する。
その後「移項」に入っていくので、こうしたまちがいはほぼ無くなります。
加えて移項の指導において、生徒がごっちゃにしないような配慮もすれば、さらにミスは減るでしょう。
では、以上の原因に配慮した指導案を見ていきましょう。
指導案
①「等式の性質①」を使って解く
ここからは、余計な項のある方程式を解いていく。
たとえばこんな問題。
$$ x-2 = 5 $$
左辺に「\(-2\)」という余計な項が入っている。
左辺から \(-2\) を消して、\(x\) だけにしたい。
どうするか?
ここで「等式の性質①」を使う。
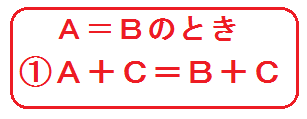
両辺に同じ数を足しても等しいままだった。
じゃあ、両辺に「\(+2\)」すれば、\(-2\) と打ち消しあう!
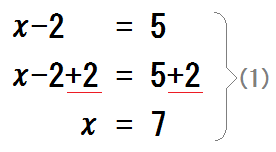
この方程式は \(x=7\) と解けた。
理解したら、(1)を丸々写そう。
写せたら、以下の問題を一緒に解いてみよう。
$$ x-3=8 \qquad x-6=-30 $$
(「両辺に何を足す?」「その式を書いて」「=は縦にそろえて書くこと」「左辺・右辺、それぞれ計算して」等と言いながら正しい途中式を書かせる)
②「等式の性質②」を使って解く
次に、こんな問題。
$$ x+4 = 1$$
左辺に「\(+4\)」 という余計な項がある。
こいつも打ち消したい。どうするか?
今度は「等式の性質②」を使う。
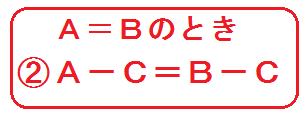
両辺から同じ数を引いても等しいままだった。
じゃあ、両辺に「\(-4\)」すれば、\(+4\) と打ち消しあう!
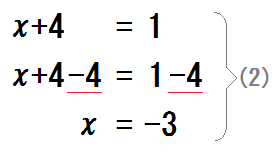
この方程式は \(x=-3\) と解けた。
理解したら、(2)を丸々写そう。
写せたら、以下の問題を一緒に解いてみよう。
$$ x+3=-4 \qquad x+6=-30 $$
(「両辺から何を引く?」「その式を書いて」「=は縦にそろえて書くこと」「左辺・右辺、それぞれ計算して」等と言いながら正しい途中式を書かせる)
③移項の導入
このように、余計な項のある方程式は、符号が逆のものを両辺に加えれば、解ける。
ただ、ちょっと面倒なんで、ちょっと省略するやり方を紹介する。
(1)式、(2)式をちょっと省略して書くと、こんなかんじ。
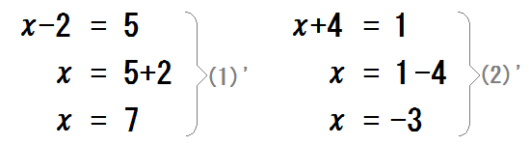
\(-2+2\) や、\(+4-4\) は、どうせ打ち消しあってなくなるからね。
そんで、いちばん上の式とまんなかの式に注目。
左辺の「\(-2\)」という項が、右辺に移って「\(+2\)」になってる、ようにみえる。
左辺の「\(+4\)」という項が、右辺に移って「\(-4\)」になってる、ようにみえる。
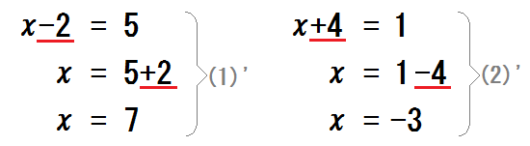
ってことは、=をまたいで項を移動させたら、符号を逆にすればいいんだ!
これを数学用語で「移項」という。
(以下を書き写させる)

この「移項」を使えば、余計な項のある方程式がちょっとカンタンに解ける。
以下の問題を、移項を使って解いてみよう。
\begin{eqnarray} & &x-3=8 \qquad x-6=-30 \\ & &x+3=-4 \qquad x+6=-30 \end{eqnarray}
(「どの項を移項させる?」「その式を書いて」「=をまたいだら符号は逆になるぞ」「計算して」等と言いながら正しい途中式を書かせる)
④ \(x\) を含んだ項のある問題
では、移項を使った応用問題。
$$ 3x=2x+6 $$
今度は右辺に \(2x\) という余計な項がある。
最後は「\(x=\)数字」の形にしたいから、この \(2x\) を、左辺に移項すればいい。
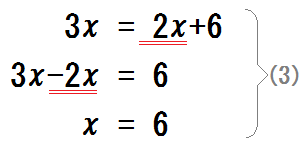
(3)を追加で書き写したら、一緒に練習問題を解いてみよう。
$$ 7x=6x-5 \qquad 4x=8+3x $$
(「どの項を移項させる?」「その式を書いて」「=をまたいだら符号は逆になるぞ」「計算して」等と言いながら正しい途中式を書かせる)
もうひとつ、応用問題。
$$ 6x+4=5x-3 $$
左辺に \(+4\) 、右辺に \(5x\) があって、それぞれ余計。
最後には「\(x=\)数字」の形にしたいから、それぞれ移項すればいい。
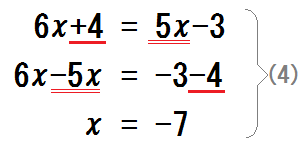
(4)を追加で書き写したら、以下の練習問題を解いてみよう。
$$2x-3=x-4 \qquad 6-8x=-7-9x $$
(「どの項を移項させる?」「その式を書いて」「=をまたいだら符号は逆になるぞ」「計算して」等と言いながら正しい途中式を書かせる)
⑤まとめと注意
ここまでの内容をまとめるよ。
余計な項がある方程式は、移項を使って解くこと。
\(x\) を含んだ項は左辺に、数字だけの項は右辺に移項させること。
そして移項したときには、必ず符号が逆になる。

(生徒のノートにこのようなまとめが出来上がる)
最後にひとつ注意点。
この2つの方程式を、それぞれ解いてみよう。
$$x+2=10 \qquad 2x=10 $$
前者は余計な項があるから、「移項」を使って解いて、「\(x=8\)」だね。
後者は左辺・右辺に項はひとつずつ。余計な項はない。
だから「\(x\) の係数を1にする」計算をして、「\(x=5\)」だね。
この2つをごっちゃにしないこと!
移項を使うのは、余計な項があるときだけ!
では、移項の説明はここまで。
たくさん練習問題を解いて、「わかる」を「できる」にしていこう。
注意点
すでに学校で、等式の性質を使った方程式の解法を習っている場合は、指導順の①②をはしょってもかまいません。
「等式の性質を使うと、こうだったね」と軽く触れてから、「③移項の導入」に進んでください。
ただ、すでに移項すら習っている場合でも、なぜ移項という操作ができるのかの説明はしたほうがいい。
「等式の性質を使った解法を、ちょっと省略しているんだ」とわかれば、生徒も自信をもって移項を使えるからです。
また、この指導案では、説明したあと「解法を正確に書き写させる」作業と、「目の前でさせてみながらアドバイスする」作業にかなり時間を使います。
これ、個別指導なら問題ないですが、集団授業だと「そんな時間はとれない!」と億劫になるかもしれません。
しかしここで時間をかけて落とし込むことで、このあとの授業がどれほどスムーズになるか。
逆にここで億劫がって、説明後に「はい、やれー」と投げちゃうと、後々どれだけ質問対応で苦労するか。
体験上、ジュウゴは骨身にしみてます。
ええ、いっぱい失敗しましたから。
生徒がこちらの望むとおりにできているか、こまかく観察して、適宜修正する。
この作業は子どものつまずきを解消するうえで絶対に必要だと考えます。
基本の計算
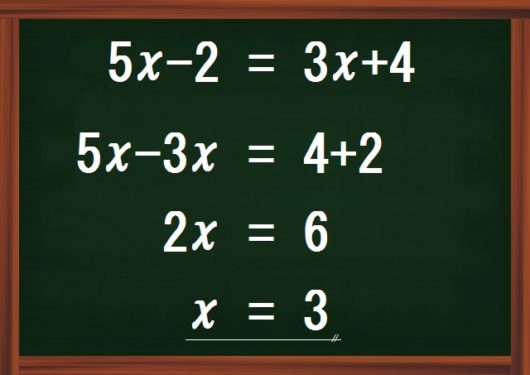
ではいよいよ、この図のような方程式の基本計算に入っていきます。
前回の内容、そして今回の前半内容がきちんとできていれば、ここでつまずくことはほぼありません。
ということは、この基本計算問題でつまずいてしまう。
その原因は、ここより前の段階のどこかにあるということなのです。
つまずく原因
1.文字式の加減計算に習熟していない
2.方程式とは何かを理解していない
3.「\(x\) の係数を1にする」計算に習熟していない
4.「移項」の計算に習熟していない
方程式の基本計算問題でつまずく原因は、以上の4つのうちどれかです。
要するに、ここに入る前の段階のどこかで、すでにつまずいているんです。
だからつまづきを解消するためには、どこでつまずいているかを明確にして、その箇所を習熟すればいい。
以下の指導案では、つまずき箇所特定のためのチェックポイントを羅列します。
生徒に試して、ひとつでも抜けていたら、そこを復習させてあげてください。
その復習をすべて終えたあと、当該内容の指導に入ります。
指導案
①「文字式の加減計算」をチェック
・\(5x-3x\) が計算できるか
・\(-4x-2x\) が計算できるか
・\(x-6x\) が計算できるか
ひとつでも欠けていたら、文字式の加減計算を復習↓
中学数学「文字と式」でつまずく原因と解決法① 文字式計算の導入
②「方程式とは何かの理解」をチェック
・「\(2x-5+6x\)」これが方程式かどうかわかるか
・等式とは何か、言えるか
・方程式の解とは何か、言えるか
・方程式とを解くとはどうこうことか、言えるか
・等式の性質5つ全部、言えるか
ひとつでも欠けていたら、方程式の最初の導入を復習↓
③「\(x\) の係数を1にする計算」をチェック
・\(3x=12\) が解けるか
・\(4x=10\) が解けるか
・\( \frac{1}{4}x=7\) が解けるか
・\( \frac{6}{5}x= -12\) が解けるか
・\(-\frac{5}{3}x= -10\) が解けるか
ひとつでも欠けていたら、\(x\) の係数を1にする計算を復習↓
④「移項の計算」をチェック
・\(x-2=5\) が解けるか
・\(x+3=-4\) が解けるか
・\(3x=2x+6\) が解けるか
・\(6x+4=5x-3\) が解けるか
・\(x+2=10\) と \(2x=10\) がどちらも正しく解けるか
ひとつでも欠けていたら、移項の計算を復習。
⑤基本計算の手順を説明
ではいよいよ、こんな方程式を解いていく。
$$5x-2=3x+4$$
解き方は、以下のとおり(目の前でやってみせる)。
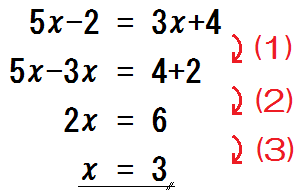
つまり、
(1) \(x\) を含んだ項は左辺へ、数字だけの項は右辺へ移項する
(2) 左辺右辺それぞれ計算して、「●\(x=\)▲」の形にまとめる
(3) \(x\) の係数を1にする
この手順でやれば、どんな方程式も解ける。
解法を書き写したら、以下の問題も一緒に解いてみよう。
$$7x+4=3x-6$$
(「移項して」「左辺右辺それぞれ計算して」「\(x\) の係数を1にして」等と言いながら、下のように正しい解法を書かせる↓)
\begin{eqnarray} 7x+4 &=& 3x-6 \\ 7x-3x &=& -6-4 \\ 4x &=& -10 \\ x &=& -\frac{5}{2} \end{eqnarray}
⑥練習
たくさん練習問題を解いて、「わかる」を「できる」にしていくこと。
注意点
見てわかるとおり、この指導案ではかなりこまかく内容を分けています。
「ここまで指導内容を細分化する必要があるのか?」とお思いの方も、あるいはいるかもしれません。
こんなに細かく積み上げる指導って、あまりみかけないですからね。
回答としては、能力の低い子ほど、より指導内容を細分化すべきです。
というのも、理解力・計算力・集中力に劣る生徒ほど、ちいさな段差でつまずくからです。
そして中1の1学期で数学につまずく中学生というのは、大なり小なりこれら能力のどれかが標準より低い場合が多い。
だから、1次方程式でつまずいている生徒には、この指導案のようにひとつひとつスモールステップで積み上げていくことをおススメします。
ちなみに、指導案の中で挙げたチェックポイント18項目。
これらは、ジュウゴの経験上、生徒がよくつまずいたポイントです。
最初は生徒たちがなぜつまずくのかわからなかったんですが、問題をよく吟味するうち、どれもそれ以前の問題とくらべて論理の展開・発展があることに気付かされました。
たとえば \(5x-3x\) と \(-4x-2x\) の間には、+-を符号と捉えるという大きな論理展開があります。
こんなつまずきポイントを何百個も、生徒から気付かせてもらいました。
これからの記事でもそんなつまずきポイントをたくさん紹介していきます。
ただ、まだまだ未熟なんで、これからも生徒の様子から学んで、増えていくでしょう。
教育に終わりはないって誰かが言ってなかったっけ。
ま、好きだからいいんだけどね。
まとめ

〇移項でつまずく
原因は以下の3つ。
- 途中式を書く習慣がない
- 正負の加減に習熟していない
- 「\(x\) の係数を1にする」計算とごっちゃ
このうち2.の場合は、正負の加減計算を復習する。
また3.の場合は、前回の記事内容を復習する。
そして1.3.に配慮した指導をすること。
指導案は以下のとおり。
- 等式の性質①を使って解く
- 等式の性質②を使って解く
- 移項の導入(数字の項のみ)
- \(x\) を含んだ項の移項
- まとめと注意
すでに学校で既習の生徒には、1.2.は簡略化してよい。
「解法を正確に書き写させる」時間と、「目の前でさせてみながらアドバイスする」時間を十分とること。
〇基本計算でつまずく
原因は以下の4つ。
- 文字式の加減計算に習熟していない
- 方程式とは何かを理解していない
- 「\(x\) の係数を1にする」計算に習熟していない
- 「移項」の計算に習熟していない
つまり、前の段階のどこかですでにつまずいている。
よってつまずき箇所を特定して復習し、その後に基本計算に入ること。
指導案は以下のとおり。
- 文字式の加減計算ができるか、3項目でチェック
- 方程式とは何か理解しているか、5項目でチェック
- 「\(x\) の係数を1にする計算」を、5項目でチェック
- 「移項の計算」を、5項目でチェック
- 基本計算の導入(手順を説明)
(1) \(x\) を含んだ項は左辺へ、数字だけの項は右辺へ移項する
(2) 左辺右辺それぞれ計算して、「●\(x=\)▲」の形にまとめる
(3) \(x\) の係数を1にする
1.2.3.4.のチェックで、どれかひとつでも欠けていたら、該当箇所を復習すること。
以上が、1次方程式の基本計算ができないという生徒向けの内容です。
子どもたちはよく、「解き方がわからない」といって質問に来ます。
でも、解き方を教えてもかれらができるようになるとは限りません。
かれらに本当に必要なのは、「わかる」から「できる」にするための習熟練習です。
よって、この指導案を元にわかりやすく説明したら、それで終わらず、たくさん問題を解かせてください。
この意味で、数学も部活や習い事といっしょ。
ボールの蹴り方をわかってもシュート練習しないと、楽譜を読めても毎日ピアノに向かわないと、できるようにはならないですもんね。
次回からは、1次方程式の応用問題を解説します。
かっこ外し・小数・分数のある計算問題。
そして、さまざまな文章題。
こうした「1次方程式の利用」について取り上げていきます。










コメント
スモールステップ、大切ですよね。
だいぶ前にテレビで、運動が苦手な子がヘディングシュートをできるようにするために、元Jリーグのサッカー選手が、スモールステップで教える(最初は、自分の頭に飛んできたボールを、ヘディングするんじゃなくて、そのボールに書かれた数字を読む、ところからはじめてたかな?)、という番組を見て(結果、全員ヘディングシュートできるようになっていました)、
運動音痴でヘディングシュートなんて一度もできたことがない私は、
自分もこういう風に習っていたら、できたかも、と思ったものでした。
運動が得意な子なら、一度手本を見せるだけで、ヘディングシュートできてしまうんだろうけど、
運動が苦手な子には、それ以前の問題(ボールが怖くて目を閉じてしまうとか)がたくさんあるので、まずはそれを解消しないといけないんですよね。
数学も同じですね。
現実には、一人一人にあったステップを用意するのは難しいなあ、と感じていますが、
理想を求めて生きたいですね。