中1数学「文字と式」の解説4回目。
今回は文字式の文章題の教え方について見ていきます。
単元名でいうと「数量の表し方」「等式の表し方」「不等式の表し方」になります。
なお「規則性」問題については、次回の記事を参照してください。
[文字と式の記事一覧]
- 文字と式①:計算の導入
- 文字と式②:途中式と分数、かっこ外し、分配法則
- 文字と式③:分数まじりの複雑な計算
- 文字と式④:数量の表し方
- 文字と式⑤:規則性の問題

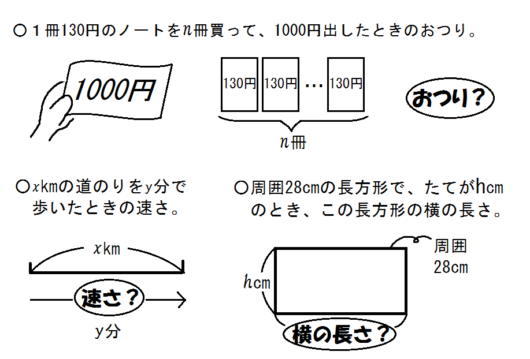
次の数量を表す式を書きなさい。
○1冊130円のノートを \(n\) 冊買って、1000円出したときのおつり。
○定価 \(a\) 円の品物を25%引きで買ったときの代金。
○\(x\) kmの道のりを \(y\) 分で歩いたときの速さ。
○男子14人の平均点が \(p\) 点、女子16人の平均点が \(q\) 点のとき、クラス全体の平均点。
○周囲28cmの長方形で、たてが \(h\) cmのとき、この長方形の横の長さ。
こんな文章問題になると、途端に「わからない」といって頭を抱える中学生が多くいます。
ここでつまずく主な原因は4つ。
それぞれ具体的に解決法を示していきます。
ひとつひとつ丁寧に指導して、生徒の「わからない」を「わかる・できる」に導いてあげてください。
(数学指導法の記事一覧はまとめページへ)
スポンサーリンク
文字の入った数量の表し方

文字式の利用において、このような文章問題にでくわすと、急に手が止まる。
そんな生徒は多くいます。
ここで考えられる原因は4つ。
- 国語力の欠如
- 単位を揃えられない
- 割合・速さ・平均・面積の求め方を忘れている
- 文字が入ると式を立てられない
1.国語力の欠如
まず、上の問題のような短い文であっても、「何を言っているのかわからない」という生徒がたまにいます。
文字が入っているためにわからないのではなくて、そもそも文章の意味がつかめない、イメージできないという子です。
これは国語力が不足していることに原因があります。
そもそも数学の文章問題というのは、すべからく国語力に依存します。
だから「文章題になるとつまずく」という生徒には、国語力をつけてあげる。
これが根本的な解決法です。
ただ、国語力をつけるには長い時間がかかります。
いま、数学の文章題でつまずいている中学生に、何か月もかけて国語の指導だけをおこなうわけにもいきません。
そこで国語力をつける指導と並行して、図でイメージを補ってあげるといいでしょう。
![]()
指導案
①読書の習慣をつけていく
いま、その子がスラスラ読めるレベルの本を準備し、読書を宿題に出す。
短文でつまずく生徒なので、小学校中学年程度からはじめるといい。
宿題の結果は「読んだ感想を言う」などで確認する。
1~2か月くらい継続する。
②読書のレベルを徐々にあげていく
すこしずつ本のレベルを上げていく。
レベルの目安は以下のとおり。
「絵本→イラスト入りの本→ライトノベル→小説」
なお、好きなジャンルがあれば何冊でも読ませていい。
また、好きな本があれば何回でもくりかえし読ませていい。
ジャンルや読書回数に制限はない。
これもやはり1~2か月くらい継続する。
③図をかいてイメージをもたせる
以上の読書指導と並行して、文章問題では図をえがいてイメージさせる。
たとえばこんなかんじ↓
これでまず、問題の意味を理解することはできるようになる。
読書指導が続いていれば、3~4か月後には、図を描かなくてもイメージできるようになってくる。
注意点
読書指導には、生徒自身の意思が不可欠です。
みずから「本を読もう」と思わないかぎり、読書なんてしないからです。
よってまず、生徒本人と、なぜ読書の習慣をつけることが大切なのか、よく話しあうといいでしょう。
また、読書指導には保護者の協力も不可欠です。
本を買うお金は保護者が出すからです。
よって本人が納得したら、つぎは保護者とも相談するといいでしょう。
保護者に会えない場合は、生徒づてに親に伝えてもらいましょう。
ここまでの内容は「文章問題の内容を理解できるようになる」ための指導です。
まずこれが出発点ですが、しかしこれだけでは「文章題ができる」ようにはなりません。
2.単位を揃えられない
例えば「分速 \(x\) mで \(y\) 時間進んだときの道のり」という問題。
これ、単位をそろえないといけない問題です。
ここで単位間の相互関係を忘れていると、問題を解くことができません。
このような単位間の相互関係はすべて、小学校で学習済みの内容です。
しかし、生徒が忘れている場合は、再度復習する必要があります。
また、単位間の相互関係を復習することで、文字の入った数量の表し方にもスムーズにつなげることができます。
指導案
①単位間の相互関係を復習する
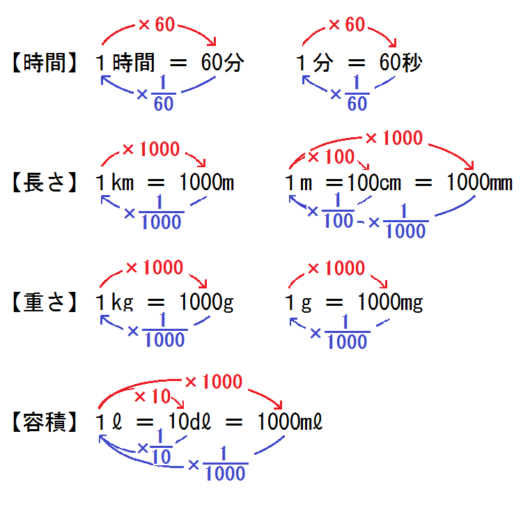
最低限、以下の4つは復習すること。
生徒に質問しながら、以下のように書いていくといい。
②単位の変換計算を復習する
以下のように矢印をかき加えて、変換するには「×●」すればいいかを示す。
③単位変換を一緒に練習する
はじめは具体的な数字で、単位変換を一緒にする。
つぎに文字におきかえて、単位変換を一緒にする。
このとき、②で出来上がった図をつねに横におきながら、生徒のヒントとするといい。
④単位変換をひとりで練習させる
数問~数十問の練習プリントを用意し、文字の入った単位変換を練習させる。
*こんな便利なサイトがありました↓ありがたいですね。
「無料で使える中学学習プリント」中1数学 文字を使った数量の表し方
注意点
時間・長さ・重さ・容積。
これら4単位のそれぞれの変換は、最低限学習すべき内容です。
このほかの単位も、問題に出てくるごとに復習するといいでしょう。
とくに「分速300m=時速18km」等とする変換は、けっこう頻出します。
文字を使った数量の表し方とはすこしずれますが、復習しておいて損はないでしょう。
また、私は変換計算は分数表記で統一しています。
「\( \times \frac{1}{1000}\)」などのようにです。
もちろん「\( \times 0.001\)」でもいいんですが、わりきれない数も出てくるので(例 \( \frac{1}{60} = 0.1666\ldots\) )、分数表記のほうがよけいな混乱がなくてすむんです。
分数か小数か迷ったら、分数にしといたほうがいいでしょう。
![]()
3.割合・速さ・平均・面積
中1文字式の文章題でつまずく原因。
その3つめは、「割合」「速さ」「平均」「図形の面積」の求め方を忘れているというものです。
この4分野は単位変換とおなじく、「学習済みだけど忘れている」可能性の高い分野。
実際、この4分野の文章問題になると、途端にわからなくなる中学生が多くいます。
そこで、この4分野の求め方をそれぞれ復習する必要がある。
加えてここでも、文字を使った文章題を同時に示すことで、現単元にスムーズにつなげていくことができます。
指導案
①割合の求め方を復習する
以下の例、以下の順番で、割合の求め方を一緒にやってみせる。
生徒が理解したら、練習問題を解かせる。
②速さ・時間・道のりの求め方を復習する
以下のように復習する。「み・は・じ」等は適宜活用する。
生徒が理解したら、練習問題を解かせる。
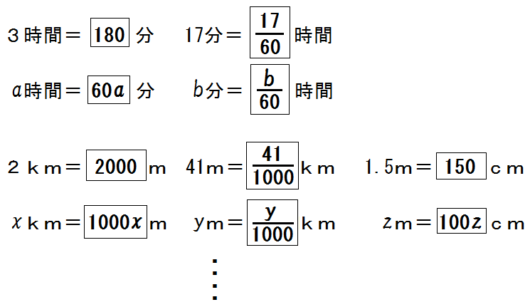
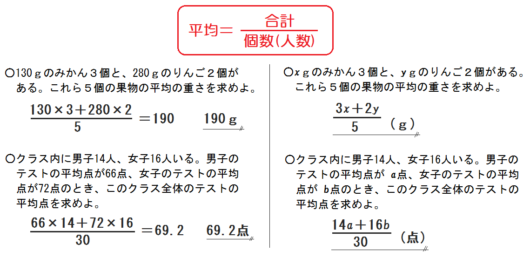
③平均の求め方を復習する
以下のように復習する。
生徒が理解したら、練習問題を解かせる。
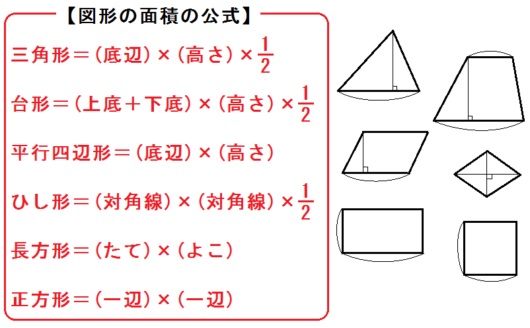
④図形の面積の求め方を復習する
まず各図形の面積の公式を復習する。
あとは①②③と同じ流れで、数字のみの問題を解く→文字の入った問題を解く、と進める。
注意点
答えの表記は、学校の先生によって多少ちがうことがあります。
以下2つほど、そんな例を挙げておきます。
数学的にはどちらでもかまいませんが、定期テストの際には学校の先生の指示にしたがいましょう。
また、指導案を見て気づいたと思いますが、4分野とも指導の流れはおなじです。
つまり「求め方を復習する」→「数字のみの文章問題を解く」→「文をほとんど変えずに、一部だけ文字にした問題を解く」という流れ。
このパターンが、最後の原因「文字が入ると式を立てられない」のところでも有効になってきます。
![]()
4.文字が入ると立式できない
あるていどの国語力はある。
単位をそろえることもできる。
割合・速さ・平均・面積の求め方も思い出した。
なのに、文字式の文章題から式を立てることができない…。
こんな中学生もいます。
こういう生徒は、文章を読んだあとに自分がどんな計算をして答えを求めようとしたか、その思考過程をみずからの意識にのぼらすことができていないのです。
これはつまり、つきつめれば「自分の客観視」「自己の対象化」「メタ認知」などのあるなしに関わってきます。中学1年生ですでに自己を客観的にみられる子もいれば、高校3年生でも主観的にしか生きられない子もいます。この違いはおそらく、自分の感情を言葉にする経験の差、そして感情を表す言葉をどれだけ知っているかという語彙の差、この2つに起因するように思います。
自己の客観視ができる生徒は数学にかぎらず学力が高くて、主観的にのみ生きる生徒は恋愛経験が豊富な印象です。どっちがいいかはわかんない。「粗忽長屋」の主人公みたいに、主観的にのみ生きる人にもあこがれるしね。
閑話休題。
そこで有効になるのは、まず文字を具体的な数字におきかえて考えること。
そして、つねに「何算する?」と発問してあげることです。
指導案
次の数量を表す式を書きなさい。
「1冊130円のノートを \(n\) 冊買って、1000円出したときのおつり」。
①文字を具体的な数字におきかえる
\(n\) 冊を \(6\) 冊などとおきかえて、一緒に求めようとしてみる。
先生「130円のノートを \(6\) 冊買った。全部で何円?」
生徒「えーっと…」
先生「いま、何算しようとしてる?」
生徒「かけ算」
先生「そうだね。式を言って」
生徒「\(130 \times 6\)」
→\( \qquad 130 \times 6\) と書く。
先生「ま、計算すると780円だ。で、1000円出したときのおつりを求める。何算すればいい?」
生徒「ひき算」
先生「そうだね。式を言って」
生徒「\(1000-780\)」
先生「そう、つなげて書くとこうだ」
→\(1000- 130 \times 6\) と書く。
②文字にもどして、立式させる
先生「では、130円のノートを \(n\) 冊買った。何算する?」
生徒「かけ算」
先生「そう。式を言って」
生徒「\(130 \times n \)」
→\( \qquad 130n \) と書く。
先生「\(130n\) 円買って、1000円出したときのおつり。何算する?」
生徒「ひき算」
先生「そう。式を言って」
生徒「\(1000-130n\)」
→\(1000-130n\) と書く。
③単位をつけて、答え
先生「最後、単位をつけ忘れるな。単位は何?」
生徒「円」
→\(1000-130n\) (円) と書く。
このように、具体的な数字でおきかえること。
そして、何算するかをつねに意識すること。
この2点に注意して文字式の文章題は解くように、と伝える。
④練習
類題を練習させる。
はじめは一緒に。
できるようになってきたら自力で。
注意点
具体的な数字でおきかえる。
何算するかをつねに意識する。
この2点を、生徒自身でできるようになることがポイントです。
よって④の段階で、一緒に問題を解いているとき、徐々に生徒自身ができるように働きかけましょう。
自立のコツは、この連載で何度も紹介したように、山本五十六大将の言葉に沿うことです↓。
また、生徒が自力でほとんど解けるようになってからも、たまに難問にぶつかって質問に来ることがあります。
「文字を使った数量の表し方」の問題は、かなり多岐にわたるからです。
そんなときも、やはりポイントは上述した2点。
「具体的な数字におきかえて考えてごらん」
「何算すればいい?」
とアドバイスしてやりましょう。
そして実は、「等式の表し方」「不等式の表し方」という単元も、指導法はまったく同じです。
具体的な数字におきかえて考える。
何算すればいいかをつねに意識する。
あとは式に、等号や不等号をつけくわえるだけです。
(不等号の意味は学習する必要があるけど)
130円のノートを \(n\) 冊買って1000円払ったら、おつりは \(m\) 円だった。
$$ \Rightarrow 1000-130n = m $$
\(x\) kmの道のりを \(y\) 分で歩いたときの速さは分速 \(z\) m未満だった。
$$ \Rightarrow \frac{1000x}{y} < z $$
もし問題文が読み取れないなら、読書指導と並行して図でイメージを。
もし単位をそろえられないなら、相互関係の復習と単位変換の計算を。
もし割合・速さ・平均・面積の求め方を忘れているなら、それぞれの復習を。
それだけで、「等式の表し方」「不等式の表し方」も乗り越えていけます。
まとめ

文字を使った数量の表し方がわからない、という生徒は…
可能性1:国語力が欠如している。
⇒読書指導と、並行して図でイメージをもたせること。
可能性2:単位を揃えられない。
⇒単位間の相互関係を復習し、単位変換の計算を示し、具体的な数字で単位変換し、そして文字でも単位変換させること。
可能性3:割合・速さ・平均・面積の求め方を忘れている。
⇒それぞれの求め方を復習し、やはり具体的な数字→文字の順で練習問題を解くこと。
可能性4:文字があると式を立てられない。
⇒具体的な数字でまず考えること。そして何算するかをつねに意識すること。
次回は中学1年数学「文字と式」の最後、規則性の問題について解説します。


















コメント
1~4のなかでは、4(立式)ができない生徒が多いと感じています。
(もっとも、基本的な問題では、1~3は問題とならないことが多いにすぎず、
1~3もできていない可能性は大いにありますが。)
・具体的な数字でおきかえる。
ことは生徒に伝えていましたが、
・何算するかをつねに意識する。
ことは伝えていませんでしたので、
今後はこちらも伝えるようにしたいと思います。