中学数学「比例と反比例」⑥　文章問題のコツ（基本・応用）

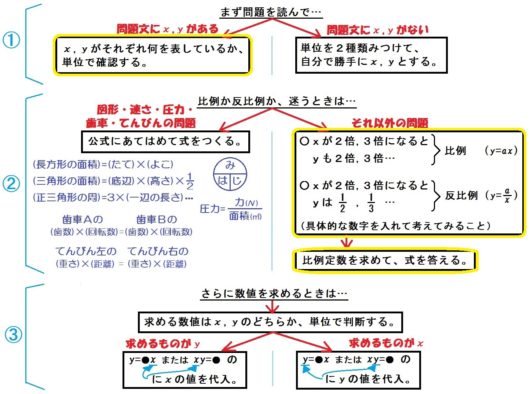
中学数学の教え方・解き方。

中１「比例と反比例」の最後は、文章問題になります。

ここでの目標。

それは、たとえ文章問題、応用問題の苦手な生徒であっても、以下のような問題が解けるようになることです。

[比例反比例の記事一覧]

1. 中１「比例と反比例」① 関数とは何か
2. 中１「比例と反比例」② 導入と用語
3. 中１「比例と反比例」③ 比例の式を求める
4. 中１「比例と反比例」④ 反比例の式を求める
5. 中１「比例と反比例」⑤ 座標とグラフ
6. 中１「比例と反比例」⑥ 文章問題(基本・応用)
7. 中１「比例と反比例」⑦ 文章問題(図形・速さ・歯車)

 

こうした文章問題は「みるだけでイヤ！」という中学生もいます。

また教える側のわれわれも、問題の種類が多岐にわたり、そのうえ解き方がひとつじゃないので、どう体系だって教えたらいいか迷うところです。

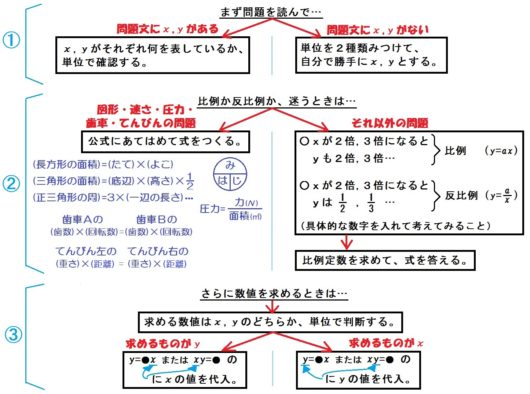
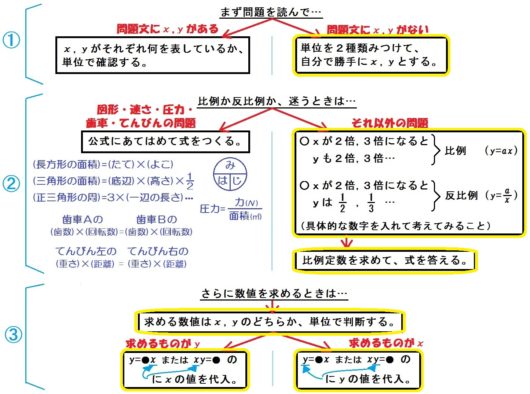
そこで、あらゆる問題に使えるフローチャートを用意しました。

このフローチャートを使えば、比例・反比例の文章問題すべてをやっつけることができます↓

じっさい、どのように使っていくのか？

「基本問題」「応用問題」「図形・動点問題」「速さ・圧力問題」「歯車・てんびん問題」の５パターンごとに、それぞれ解説していきます。

この指導をつうじて、中学生が比例・反比例の文章問題にたいする苦手意識を克服するとともに、文章問題に出合ったときのコツや思考過程を身につけてほしいと思います。

ではいきましょー。

比例・反比例の文章問題　基本

まず文章問題の基本です。

問１のような問題で困るのは、式を立てるとき「比例か反比例か迷う」ってトコロ。

でも大丈夫。フローチャートどおりにやれば解けます。

なぜなら問１の４問はすべて

• 問題文に \(x\) , \(y\) がある
• 公式のない、それ以外の問題

です。

よって、フローチャートにあるとおり、

• \(x\) が\(2\)倍,\(3\)倍…になると \(y\) も\(2\)倍,\(3\)倍…⇒比例
• \(x\) が\(2\)倍,\(3\)倍…になると \(y\) は\(\frac{1}{2}\) , \(\frac{1}{3}\) …⇒反比例

これで判断すればいいんです。

 

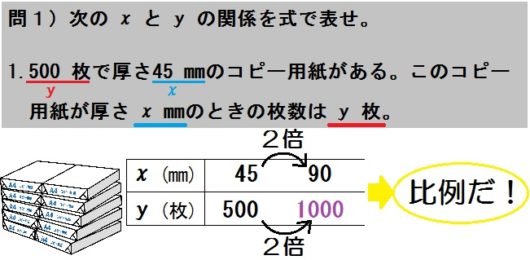
コピー用紙の問題

はじめに、問題文に \(x\) と \(y\) があるので、それぞれ何を表しているか確認します。

コツは、単位をみること。

\(x\) の単位が「mm」なので、厚さを。

\(y\) の単位が「枚」なので、枚数を、それぞれ表しています。

また \(45\) mmという数は \(x\) の数値であること。

\(500\) 枚という数は \(y\) の数値であることも、やはり単位でわかります。

単位を確認せずに \(x=500\) で \(y=45\) だと、文章の並びだけで判断しないように。こういうミス、中学生はけっこうやります。

 

つぎに、この問題は「厚さと枚数の関係」なので、公式を使わない、それ以外の問題です。

そこで、上述したように、

• \(x\) が\(2\)倍,\(3\)倍…になると \(y\) も\(2\)倍,\(3\)倍…⇒比例
• \(x\) が\(2\)倍,\(3\)倍…になると \(y\) は\(\frac{1}{2}\) , \(\frac{1}{3}\) …⇒反比例

これで比例か反比例かを判断します。

コツは、\(x\) と \(y\) に具体的な数を入れて考えてみること。

たとえば \(x\) が \(45\) mmのとき、\(y\) は \(500\) 枚。

じゃ、\(x\) が２倍の \(90\) mmになったら？

つまりコピー用紙の厚さが倍になったら、枚数は２倍？それとも \(\frac{1}{2}\) ？

そう、\(y\) は２倍の \(1000\) 枚になります。

よって、この問題における \(x\) と \(y\) の関係は比例だとわかるんです。

 

ここまでくれば、問１の1.は以下のように書きかえられます。

比例の式は \(y=ax\) 。

比例定数は \(a= \frac{y}{x}\) で求められました。

よって、

$$ a= \frac{500}{45} = \frac{100}{9} $$

$$ \mbox{答．} y=\frac{100}{9}x $$

[関連記事]
「比例と反比例」③ 比例の式を求める

 

このように、まず単位で \(x\) と \(y\) を確認。

つぎに比例か反比例か迷うときには、

• \(x\) が\(2\)倍,\(3\)倍…になると \(y\) も\(2\)倍,\(3\)倍…⇒比例
• \(x\) が\(2\)倍,\(3\)倍…になると \(y\) は\(\frac{1}{2}\) , \(\frac{1}{3}\) …⇒反比例

具体的な数を入れて、これを考えてみる。

以上が基本問題のコツです。

 

 

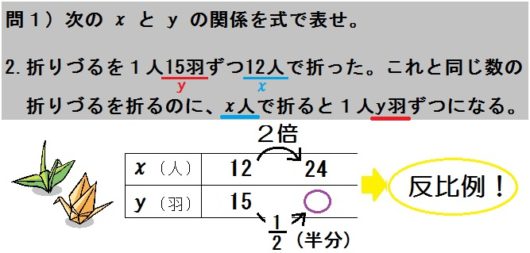
折りづるを分担する問題

同じ流れで、問１の2.もやってみます。

まず問題文に \(x\) と \(y\) があるので、それぞれ何を表しているか、単位で確認します。

\(x\) は「人」なので、人数。

\(y\) は「羽」なので、１人あたり折りづるを折る数。

また \(12\) 人のほうが \(x\) の数値。

\(15\) 羽のほうが \(y\) の数値です。

 

つぎに、この問題も公式はないので、

• \(x\) が\(2\)倍,\(3\)倍…になると \(y\) も\(2\)倍,\(3\)倍…⇒比例
• \(x\) が\(2\)倍,\(3\)倍…になると \(y\) は\(\frac{1}{2}\) , \(\frac{1}{3}\) …⇒反比例

これで、具体的な数字を入れて、比例か反比例か判断します。

\(x\) が２倍の \(24\) 人になったら？

つまり人数が倍になったら、１人あたりの折る数は２倍？それとも \(\frac{1}{2}\) ？

そう、 \(\frac{1}{2}\) になりますね。

だから、この問題は反比例だとわかるんです。

（\(\frac{15}{2}\) 羽ってなんやねん、ってのは置いといてかまいません。ここでは比例か反比例かさえわかればいいんで。）

 

反比例の式は \(y=\frac{a}{x}\) 。

比例定数は \(a= xy\) で求められました。

よって、

$$ a= 12 \times 15 = 180 $$

$$ \mbox{答．} y=\frac{180}{x} $$

となります。

[関連記事]
「比例と反比例」④ 反比例の式を求める

 

 

牛肉の問題

問１の3.と4.も流れは同じです。

詳細は省きます、

3.は比例。よって、

$$ a= \frac{250}{100} = \frac{5}{2} $$

$$ \mbox{答．} y=\frac{5}{2}x $$

また4.は反比例。よって、

$$ a= 100 \times 2000 = 200000 $$

$$ \mbox{答．} y=\frac{200000}{x} $$

 

なお「4.の問題がわからない」という人は具体的な数字を入れて考えてみましょう。

\(100\) gあたり \(200\) 円の牛肉は、\(2000\) 円で何g買える？

→\(1000\) g。（ \(200 \div 100=2\mbox{円/g} \quad 2000 \div 2=1000\mbox{g}\) ）

\(100\) gあたり \(400\) 円の牛肉は、\(2000\) 円で何g買える？

→\(500\) g。（ \(400 \div 100=4\mbox{円/g} \quad 2000 \div 4=500\mbox{g}\) ）

つまり、\(x\) が倍になれば \(y\) は半分になるので、反比例。

このようにして判断しましょう。

 

以上、比例・反比例の文章問題の基本。

つまり、

①「問題文に \(x\) と \(y\) があるから」
↓
 \(x\) , \(y\) がそれぞれ何か、単位で確認。

②「公式以外の問題だから」
↓
・\(x\) が\(2\)倍,\(3\)倍になると \(y\) も\(2\)倍,\(3\)倍 ⇒比例
・\(x\) が\(2\)倍,\(3\)倍になると \(y\) は\(\frac{1}{2}\) , \(\frac{1}{3}\) ⇒反比例
で判断する。

という流れの問題でした。

＞Amazonプライム・ビデオ「孤独のグルメ」

 

比例・反比例の文章問題　応用

基本のつぎは、文章問題の応用です。

つまり、この問２問３のように、

• 問題文に \(x\) と \(y\) がない
• やはり公式を使う問題ではない
• 「\(x\) と \(y\) の関係式」じゃなくて何かの数値を求める

という特徴をもった問題です。

これをフローチャートに当てはめると、以下の黄色の部分になります。

この３段階で、問題を解いていきます。

 

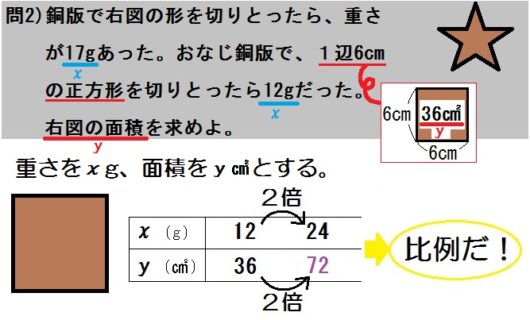
銅板の重さと面積の問題

【第１段階】

この問題、文中に \(x\) と \(y\) がありません。

また「重さ(g)」と「面積(㎠)」という２種類の単位があります。

よって、好きなほうをえらんで \(x\) , \(y\) とします。

ここでは仮に、重さを \(x\)g、面積を \(y\)㎠ としておきます。

（もちろん逆でもかまいません。）

「おいおいジュウゴ、おまえアホか。１辺 \(6\) cmってあるだろう。「長さ」もふくめて単位は合計３種類だろが。」

わたしがアホなのはまちがいありませんが、この問題は、２種類でいいんです。つまり「cm」って長さの単位は無視していいんです。なぜなら関数というものは２種類の数量しか扱えないからです。３種類以上になったら、お手上げなんです（少なくとも中学・高校の数学までは。媒介変数とかは置いといて）。

んで、よく問題文を読むと、「１辺 \(6\) cmの正方形」とあります。ピンときたでしょう。

そう、正方形の面積が \(6 \times 6=36\) ㎠だと。

だからこの問２に出てくる単位は「重さ(g)」と「面積(㎠)」の２種類、としていいのです。

 

【第２段階】

いま対応しているのは \(12\)gで \(36\)㎠ という関係です。

つまり \(x=12\) のとき \(y=36\) 。

ここで、\(x\) が２倍になったら？

つまり重さが倍の \(24\)gになったら、面積は２倍？それとも \(\frac{1}{2}\) ？

そう、倍になりますね。

よってこの問題は比例の関係だとわかります。

比例の式は \(y=ax\) 。

比例定数は \(a= \frac{y}{x}\) で求められるので、

$$ a= \frac{36}{12} = 3 $$

$$ \mbox{関係式．} y=3x $$

とわかります。

 

【第３段階】

これで終わりじゃありません。

問２で求めるものは、重さ \(17\)gの星形の面積です。

これは、言いかえると、こんな問題になります。

比例の式を求めるの後半でやりましたね。

出てきた式に \(x=17\) を代入すればいいと。

だから \(y=3x\) に \(x=17\) を代入して、

\begin{eqnarray} y &=& 3 \times 17 \\ y &=& 51 \end{eqnarray}

答．\(51\) ㎠

 

以上のように３段階で解いていく。

これが銅版の重さと面積などの、応用問題の流れ・コツです。

 

 

水を入れる問題

同じ流れで、問３の水を入れる問題も解いていきます。

【第１段階】

まず問題文に \(x\) と \(y\) がないので、単位を２種類みつけます。

「毎分水を入れる量(L)」と「時間(分)」ですね。

この２つを好きに \(x\) , \(y\) とします。

ここでは毎分水を入れる量を \(x\) L、時間を \(y\) 分としておきます。

（もちろん逆でもかまいません）

 

【第２段階】

対応しているのは、毎分 \(5\) Lずつで \(12\) 分という関係。

つまり \(x=5\) のとき \(y=12\) 。

ここで、\(x\) が２倍になったら？

つまり毎分 \(10\)Lずつ水を入れたら、いっぱいになる時間は２倍？それとも \(\frac{1}{2}\) ？

そう、 \(\frac{1}{2}\) 、半分になりますね。

よってこの問題は反比例の関係だとわかります。

反比例の式は \(y=\frac{a}{x}\) 。

比例定数は \(a= xy\) で求められるので、

$$ a= 5 \times 12 = 60 $$

 

【第３段階】

さいご、関係式にわかってるほうを代入します。

ここで注意点が２つ。

わかっている \(15\) 分というのは、\(x\) と \(y\) どっちの値か？

そう、 \(y\) です。

だから関係式に代入するのは \(y=15\) のほう。

なんとなく \(x\) に \(15\) を代入しちゃう中学生が多いので、注意してください。

 

そしてもうひとつの注意点は、代入先の関係式は

$$ y=\frac{60}{x} \ \mbox{よりも} \quad xy=60 \ \mbox{のほうがラク}$$

という点。

（くわしくは反比例の式を求める後半で解説しています）

以上２つに注意して解くと、

 

このように、比例・反比例の文章問題の応用では、

①「問題文に \(x\) と \(y\) がないから」
↓
単位を２種類みつけて好きに \(x\) , \(y\) とする。

②「公式以外の問題なら、やはり」
↓
・\(x\) が\(2\)倍,\(3\)倍になると \(y\) も\(2\)倍,\(3\)倍 ⇒比例
・\(x\) が\(2\)倍,\(3\)倍になると \(y\) は\(\frac{1}{2}\) , \(\frac{1}{3}\) ⇒反比例
で判断する。

③「求める数値は \(x\) と \(y\) のどっちかに注意して」
↓
・比例なら \(y=ax\) の式に
・反比例なら \(xy=a\) の式に
わかってるほうを代入して、もう片方を求める。

という３段階で解きましょう。

＞Amazonプライム・ビデオ「孤独のグルメ Season2」

 

ここまでのまとめ

いったんまとめます。

中１数学「比例と反比例」の文章題。

基本および応用問題は、以下のフローチャートどおりに解くこと。

とくに、コツは以下の２つ。

○どっちが \(x\) でどっちが \(y\) か迷うときには、単位で判断すること。

○また、比例か反比例か迷うときには、

• \(x\) が\(2\)倍,\(3\)倍…になると \(y\) も\(2\)倍,\(3\)倍…⇒比例
• \(x\) が\(2\)倍,\(3\)倍…になると \(y\) は\(\frac{1}{2}\) , \(\frac{1}{3}\) …⇒反比例

 

→中学数学「比例と反比例」⑦　文章問題のコツ（図形・速さ・歯車）

 

 

なお、以上の指導はあくまで「比例・反比例の文章問題が苦手」という生徒を想定したものです。

文章を読んで、すぐ立式できるような生徒へは必要ありません。

「全然わからない」

「わたしバカなんかな」

「もう何がわからんかもわからん」…。

こういって自信とヤル気を失っている中学生にこそ、ここでのノウハウを使ってあげてください。

 

つづけて、「比例と反比例」文章問題のうち、

• 図形、動点の問題
• 速さ、圧力の問題
• 歯車、てんびんの問題

をやっつけます。

→中学数学「比例と反比例」⑦　文章問題のコツ（図形・速さ・歯車）