中1数学「比例と反比例」の教え方3回目。
今回から比例の式を求める問題、反比例の式を求める問題の教え方です。
[比例反比例の記事一覧]
ここでの最終目標。
それは、以下のような問題が解けることです。
例5) \(y\) は \(x\) に比例し、\(x=4\) のとき \(y=6\) である。\(y=-3\) のときの \(x\) の値を求めよ。(2017香川改)
答. \(x=-2\)
例10) \(y\) は \(x\) に反比例し、\(x= \frac{10}{3}\) のとき \(y= – \frac{12}{5}\) である。\(x= \frac{1}{2}\) のときの \(y\) の値を求めよ。
答. \(y=-16\)
この2問がどちらも解けるなら、比例・反比例の式を求める問題はバッチリです。
もし解けないのなら、解けるようになるためのステップをここで解説します。
比例・反比例の式を求める問題ができない、わからない。
つまり比例・反比例の式でつまずく原因は、3つあります。
①比例・反比例の式をおぼえていない
②代入という操作が正しくできない
③ \(a= \frac{y}{x}\) 、\(a=xy\) を知らない
①の中学生は、問題を読んで「何をしたらいいのかわからない」となります。
②の中学生は、例題5)が正しくできません。
③の中学生は、例題10)ができず、難関私立入試などで後れをとることになります。
とくに②と③はどちらもできることが、偏差値50以上の高校をねらう場合に重要となります。
しかしなぜか、教科書や参考書はじめほとんどの教え方は②と③どちらの原因も取り除くことはしません。
つまり、比例の式の求め方として、
「 \(y=ax\) の式に \(x\) と \(y\) の値を代入すればいい」
「 \(a= \frac{y}{x}\) で比例定数を求めればいい」
このどちらかしか教えないんです。
生徒の混乱を避けるためだと思いますが、これでは片手落ちです。
そこでここでは、まず①の原因をとりのぞいて、そのあと②と③どちらもできるような指導を示します。
定期テストで平均以下をとる生徒から、難関私立をめざす生徒まで、幅広くカバーする指導方法となります。
塾講師や家庭教師の方、中学生の保護者の方、どうぞご参考ください。
比例の式を求める

まずは比例の式を求める基本問題から。
ここでは、基本の解き方をおさえつつ、次につながる知識すべてをわかりやすく生徒に落とし込んでいくことが大切です。
指導案(前半)
1.前回、\(y= \mbox{(xを使った式)}\) が関数の式だと習った。
そのなかでも、こんな形をした関数の式、
$$ y=2x \qquad y=30x $$
$$ y= -5x \qquad y= \frac{1}{4}x \quad \ldots$$
つまり \(y=ax\) ( \(a\) には数字が入る)の形の関数を比例という。
んで、こういう形の関数式なら、「 \(y\) は \(x\) に比例する」という。
逆に、\(y\) が \(x\) に比例するなら、式の形は「 \(y=ax\) 」ってこと。
(ちなみに \(a\) に入る数字にも名前があって、「比例定数」という。)
[前回の記事→]中学数学「比例と反比例」の教え方② 関数の導入と用語の説明
2.では問題を解いてみよう。
例1)\(y\) は \(x\) に比例し、\(x=2\) のとき \(y=-6\) である。\(y\) を \(x\) の式で表せ。
この問題、「 \(y\) を \(x\) の式で表せ」とあるから、答えは関数の式だ。
しかも文の最初に「 \(y\) は \(x\) に比例し」とあるから、答えの形は \(y=ax\) だ。
だから、あとは \(a\) に入る数字さえわかればいい。

じゃあ、どうするか?
ここで「 \(x=2\) のとき \(y=-6\) である」を使う。
\(x\) が2のとき \(y\) が-6ってある。
よって、\(y=ax\) という等式の \(x\) のところに \(2\) を、\(y\) のところに \(-6\) を当てはめればいい。
つまり、\(y=ax\) という等式の \(x\) と \(y\) を、\(2\) と \(-6\) に代えてやる。
ようするに選手交代。
この、文字から数字への選手交代を「代入」といった。

3.さて、\(-6=2a\) という等式になった。
( \(-6=a2\) じゃヘンだから \(a\) と \(2\) は入れ替えてる)
これ、\(a\) の方程式だ。
だから解けばいい。
\begin{eqnarray} -6 &=& 2a \\ 2a &=& -6 \\ a&=& -3 \end{eqnarray}
こうして、\(a\) に入る数字が \(-3\) とわかった。
[参考記事→]中1「1次方程式」でつまずく原因と解決法① 導入
4.これで終わりじゃない。
「 \(y\) を \(x\) の式で表せ」と言われてるから、式の形で答えなきゃ。
\(y=ax\) の \(a\) の代わりに \(-3\) を入れて、答えは、
$$ y=-3x $$

5.このように、
\(y=ax\) の \(x\) と \(y\) のところに数字を代入して \(a\) を求める。
これが、比例の式を求める問題の基本の解き方。
指導案(後半)
6.では、例題2と例題3を一緒に解いてみよう。
例2)\(y\) は \(x\) に比例し、\(x=7\) のとき \(y=4\) である。\(y\) を \(x\) の式で表せ。
解)\(y=ax\) に \(x=7\) 、\(y=4\) を代入して
\begin{eqnarray} 4 &=& 7a \\ 7a &=& 4 \\ a&=& \frac{4}{7} \end{eqnarray}
答.\(y= \frac{4}{7}x \)
例3)\(y\) は \(x\) に比例し、\(x=5\) のとき \(y= \frac{10}{3}\) である。\(y\) を \(x\) の式で表せ。
解)\(y=ax\) に \(x=5\) 、\(y=\frac{10}{3}\) を代入して
\begin{eqnarray} \frac{10}{3} &=& 5a \\ 5a &=& \frac{10}{3} \\ a&=& \frac{2}{3} \end{eqnarray}
答.\(y= \frac{2}{3}x \)
7.さて、基本の解き方がわかったところで、ひとつ裏ワザを教える。
比例定数 \(a\) をもっとラクに求める裏ワザだ。
どんな裏ワザかというと、ヒントはこれ。
例1)\(x=2\) 、\(y=-6\) ⇒比例定数 \(a= -3\)
例2)\(x=7\) 、\(y=4\) ⇒比例定数 \(a= \frac{4}{7}\)
例3)\(x=5\) 、\(y= \frac{10}{3}\) ⇒比例定数 \(a= \frac{10}{3} \div 5 = \frac{2}{3}\)
気づいた?
$$ a= \frac{y}{x} \quad ( y \div x ) $$
これが裏ワザ。
今後、\(y=ax\) の \(a\) を求めるときには、この
$$ a= \frac{y}{x} \quad ( y \div x ) $$
を使っていい。
8.ここまでをまとめよう。
比例の式を求める問題では、
○ \(y=ax\) の \(x\) と \(y\) に数字を代入して \(a\) を求める。
○ \( a= \frac{y}{x} \quad ( y \div x ) \) を使って \(a\) を求める。
この2つの方法があるということ。
じゃあ、たくさん問題を解いて「わかる」を「できる」にしていこう。
注意点
冒頭、比例とは何かを導入したあとに、
「逆に、\(y\) が \(x\) に比例するなら、式の形は『 \(y=ax\) 』ってこと」
この一言を忘れない。
これがひとつめの注意点です。
この一言がないと、論理のステップがひとつ飛んでしまいます。
つまり「 \(y=ax\) 」⇒「 \(y\) は \(x\) に比例する」は言っても、
「 \(y\) は \(x\) に比例する」⇒「 \(y=ax\) 」は言ってないことになる。
(ようするに必要条件だけじゃなく十分条件でもある)。
結果として、問題を解くときに生徒が悩むことになるので、忘れやすいですが注意しましょう。
また、例題2、3を一緒に解く際に、
「 \(y=ax\) に \(x=7\) 、\(y=4\) を代入して」
この一文も生徒に書かせること。
これがもうひとつの注意点です。
というのも、どこに何を代入したのか書くクセをつけておかないと、このさき以下のような間違いを犯すからです。
問)\(y=2x\) のグラフ上に点(□、10)があるとき、□に当てはまる数を求めよ。
解)\(2 \times 10 = 20\) 答.\(20\) ←まちがい
代入という操作が正しくできないとは、このような状態をいいます。
どこに、何を代入するべきか、わからなくなる。
こういうことのないように、最初の一文も書かせましょう。
これは中2の一次関数にも、中3や高1の二次関数にもつながる大切な注意点です。
比例の式を求めてさらに…

次に、比例の式を求める問題の応用です。
ここでは、問題を2つに分けることがコツになります。
指導案
1.では、比例の式を求める問題の応用版を解いてみよう。
例4)\(y\) は \(x\) に比例し、\(x=2\) のとき \(y=-8\) である。\(x=-1\) のときの \(y\) の値を求めよ。
(2017栃木県公立高校入試問題)
一見ごちゃごちゃしてるけど、こういう問題もコツをつかめばむずかしくない。
コツは、問題文を前半と後半に分けることだ。

つまり、こういうこと。
例4の前半)\(y\) は \(x\) に比例し、\(x=2\) のとき \(y=-8\) である。( \(y\) を \(x\) の式で表せ。)
例4の後半)(出てきた式において、) \(x=-1\) のときの \(y\) の値を求めよ。
2.例4の前半は、もうできるね。
\(y=ax\) の \(x\) と \(y\) に数字を代入して \(a\) を求めてもいいし、
\( a= \frac{y}{x} \quad ( y \div x ) \) を使って \(a\) を求めてもいい。

どっちで解いても、\(y= -4x \) と式が出る。
3.式が出たら、つぎは例4の後半だ。
式が出てて、\(x\) も \(-1\) とわかってて、あと \(y\) の値がほしい。
じゃあ \(y=-4x\) っていう式に \(x=-1\) を当てはめればいい。つまり代入だ。

こうして \(y=4\) と答えがでる。
4.おなじやり方で、例題5を一緒に解いてみよう。
コツはやっぱり、問題を前半と後半に分けることね。
例5)\(y\) は \(x\) に比例し、\(x=4\) のとき \(y=6\) である。\(y=-3\) のときの \(x\) の値を求めよ。
(2017香川県公立高校入試問題を一部改訂)解)\(a= \frac{6}{4} = \frac{3}{2}\)
\(y= \frac{3}{2}x\) に \(y=-3\) を代入して
\begin{eqnarray} -3 &=& \frac{3}{2}x \\ \frac{3}{2}x &=& -3 \\ x&=& -2 \end{eqnarray}
答.\(x= -2\)
後半、注意すべきは、\(y\) がわかってて \(x\) がわからないんだから、式に代入するのは \(y\) の方ってトコ。
それで、\(-3= \frac{3}{2}x\) という \(x\) の方程式を解く。
どっちに代入するのかはまちがえやすい。
だからこそ、「 \(y= \frac{3}{2}x\) に \(y=-3\) を代入して」という言葉は書いておこう。
5.これで、応用問題のやり方もわかったね。
まとめよう。
コツは問題文を前半と後半に分けること。
後半は \(x\) か \(y\) のうち、わかってる方を式に代入してもう一方を求める。
じゃ、たくさん問題を解いて「わかる」を「できる」にしていこう。
注意点
ここでもやはり、
「 \(y= -4x\) に \(x=-1\) を代入して」
「 \(y= \frac{3}{2}x\) に \(y=-3\) を代入して」
こうした一文を書かせること。
これが注意点のひとつです。
理由はやはり、指導案のなかでも言いましたが、どっちに代入するか間違えやすいからです。
そしてここでの注意点のもうひとつは、生徒が慣れてきたら、比例定数の求め方は
$$ a= \frac{y}{x} \quad ( y \div x ) $$
こっち優先で使うことです。
理由はふたつあって、解答欄がごちゃごちゃするのを避けるため。
そして、こっちの求め方のほうがより早く解けるためです。
これは比例だけでなく、反比例の比例定数の求め方( \(a=xy\) )でも同様です。
慣れてきたなら、一発で比例定数を出したほうがいいんです。
以上2つの注意点が活きる場面を、ひとつ紹介しましょう。
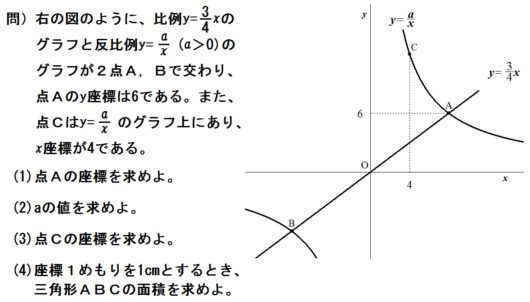
定期テストや中学生模試、あるいは問題集などでよくみかけるのが、こんな問題です↓
時間がある方はぜひ解いてみてください。
これ、(1)~(3)は基本問題で、(4)のみが難問です。
基本問題において、正確に代入できることがいかに大切か、わかるはずです。
そして比例定数がパッと瞬時に出ないと、(4)をじっくり考える時間が足りなくなることにも、気づくはずです。
だからこその、上記ふたつの注意点なのです。
ちなみに解答は以下のとおり。
(1)A(8,6) (2) \(a=48\) (3)C(4,12) (4)72㎠
(4)の解き方については「比例と反比例」⑤の記事で解説します。
まとめ

比例の式を求める問題ができない・わからない理由は3つ。
①比例の式 \(y=ax\) をおぼえていない
②代入という操作が正しくできない
③ \(a= \frac{y}{x}\) を知らない
よってまず比例の式をいろいろ示す。
そして、\(y\) が \(x\) に比例するなら式の形は「 \(y=ax\) 」だとも付け加える。
![]()
こうした基本問題を解く方法は2つ。
① \(y=ax\) の \(x\) と \(y\) のところに数字を代入して \(a\) を求める。
② \( a= \frac{y}{x} \quad ( y \div x ) \) を使って \(a\) を求める。
方法①を使う際には「…に~を代入して」という一文を書かせること。
こうした応用問題では、問題を前半と後半に分けることがコツ。
後半ではやはり、「…に~を代入して」という一文を書かせること。
そして前半では \( a= \frac{y}{x} \quad ( y \div x ) \) を使って、パッと解くように指導していくこと。
次回は反比例の式を求める問題の指導方法です。
反比例も、比例とほぼ同じ教え方になりますが、比例定数のカンタンな求め方 \(a=xy\) がより重要になってきます。
なぜならこの記事の冒頭で示した例題10、
このような問題が、代入の方法では解けなくなるからです。
[比例反比例の記事一覧]








コメント
比例や反比例の表の特徴
比例だとxが○倍になるとyも○倍 、商が比例定数で一定
反比例だとxが○倍になるとyは1/○、積が比例定数で一定
といった事はやらないのでしょうか?
座標からグラフの導入まで、これらに触れていなさそうなので
連立方程式の最初のところに、
>中学2年生の春から夏にかけて学校で習う連立方程式。
>子どもたちがこれからも数学好き・数学できる人となるために、この単元でもっとも養>うべき能力とは何か?
>それは記述式の解答を論理だてて書ききる力です。
とあります。
しかし、この比例の式を求めるところでも、
①y=axとおく
②y=axにx、yの値を代入する
③aの一次方程式を解く
④求めたaをy=axに代入する
といった記述が必要となり
「解答を論理だてて書ききる力」が必要だと感じています。
例えば、以前、上記の①~③はできても、
なぜか、④のところで止まってしまう生徒がいました。
「解答を論理だてて書ききる力」を、
比例のところではなく、
連立方程式のところに持ってきたのは、なぜでしょうか?
※追申
いつもつまらないことばかり書いていますが、
本当にこのサイトは素晴らしいと感じています。
メインターゲットは指導者向けなのでしょうが、
このサイトを見ている中学生も結構いるのではないかと思います。
今、新型コロナウイルスの影響で、自宅学習を余儀なくされている生徒も多い中、
このサイトは、生徒の学習に大いに役立っていることでしょう。
これからも影ながら応援しています。
>「解答を論理だてて書ききる力」を、
比例のところではなく、
連立方程式のところに持ってきたのは、なぜでしょうか?
理由は以下4点です。
1.比例の計算だと、暗算力のある生徒はいっぱつで答えを出しちゃうから(a=y/xを使うならなおさら)。
2.連立方程式の解答の記述は、これまででいちばん長く、考えるべきことも多いから(解答パターンがひとつじゃない)。
3.連立方程式の前に、式による説明という単元があるから(論理だてて書く訓練を直前にしていることになる)。
4.連立方程式の後に、一次関数の利用や図形の証明という単元があるから(論理だてて書く力がないと点数が取れない)。
以上の理由から、連立方程式単元で「解答を論理だてて書ききる力」に重点を置いています。
もちろん指導に正解はないので、あくまでジュウゴの指導方針です。
コロナ禍のいま、このサイトがすこしでもお役に立っていれば幸いですね。ありがとうございます。