中1数学「空間図形」の3回目です。
今回は体積の問題で中学生がつまずきやすいところを解説します。
柱・錐・球それぞれ、入試問題中心に計6例題。
ぜんぶ応用問題ですので、基本を学んだうえで「でも、じっさいのテストになるとできない」って生徒にご参考ください。(とくに例題6の富山入試は難問です)
練習問題もつけたので、ここで紹介するコツをさっそく試す機会としてどうぞ。
では、いざ。
≪「空間図形」の記事一覧≫
柱の体積

柱ってのは、底面が垂直に動いてできた立体のこと。
イメージとしては、パンケーキをかさねていったら円柱、サンドイッチをならべていったら三角柱です。
ここから
$$ \mbox{柱の体積} = \mbox{(底面積)} \times \mbox{(高さ)} $$
という公式が生まれます。
こうしたイメージをもとに、応用問題を解いていきましょう。
横になってても柱
例題1のポイントは「この立体が四角柱だ!」と見抜けるかどうか。
つまり台形BFGC(またはAEHD)が底面だとイメージできるかです。
イメージできる人にとっては当たり前ですが、意外とこういう横になってる柱を見落とす中学生が多い。
サンドイッチの例でも言ったように、同じ面がずおおぉーっと伸びていたら、縦でも横でも斜めでも柱です。
「柱って縦に伸びたやつ」と思ってる人は、この機会にイメージを改めてください。
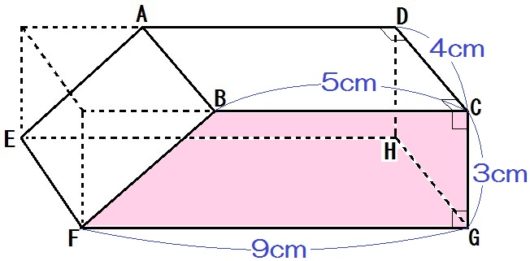
ってことで、解答は以下のとおり。
\begin{eqnarray} & &(5+9) \times 3 \times \frac{1}{2} \times 4 \\ &=& 84 \end{eqnarray}
答.84㎤
なお、底面積だけ先に求めて
\begin{eqnarray} & &(5+9) \times 3 \times \frac{1}{2} = 21 \\ & & 21 \times 4 = 84 \end{eqnarray}
という式でもOKです。
ただジュウゴは式をぜんぶつなげて書くほうをおススメします。
なぜならつなげて書くと計算がラクになる場合があるから(約分できたり、分配法則の逆が使えたり)。
このことは高校生になるとより実感するので、中学のうちから身につけておくといいでしょう。
[関連記事]
三角形の面積を求める公式7選。高校数学のまとめにどうぞ
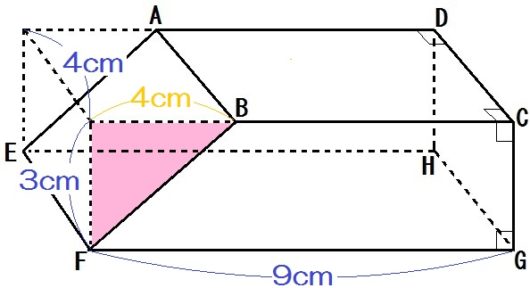
ちなみに例題1には別解があります。
「直方体-三角柱」で出す方法。こちらは
\begin{eqnarray} & & 4 \times 9 \times 3 \ – \ 4 \times 3 \times \frac{1}{2} \\ &=& 108 – 24 \\ &=& 84 \end{eqnarray}
答.84㎤
という求め方になります。
いずれにしても、横になってても柱というポイントを押さえましょう。
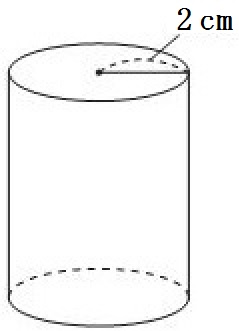
高さを求める問題
この例題2のような高さを求める問題では、自分で方程式をつくって解くというのがポイントです。
つまり、以下のとおり。
求める高さを \(h\) cmとすると、
\begin{eqnarray} 2 \times 2 \times \pi \times h &=& 24 \pi \\ 4 \pi h &=& 24 \pi \\ h &=& 6 \end{eqnarray}
答.6cm
[関連記事]
中学数学「1次方程式」文章題の解き方①【代金、個数】
もちろん方程式ではなく、
\begin{eqnarray} & & 2 \times 2 \times \pi = 4 \pi \\ & & 24 \pi \div 4 \pi = 6 \end{eqnarray}
と求めることもできます。
しかし、算数でなく数学ができるようになりたいなら、「未知数を文字でおいて方程式をつくる」という意識を常日頃からもっておくことが大切です。
なぜなら現代日本の中学・高校・大学数学は、和算の伝統じゃなく西欧文明の延長上にあるから。
高さを求める問題を後者の方法でやってる人は、この機会に、つるかめ算的な発想から代数的な発想に切りかえてください。
そのほうが高校入試や高校数学につながります。
ま、当ブログの「方程式文章題」記事を読んでる人は問題ないですね。
[関連記事]
練習問題
では、練習問題です。
例題1,2を参考にしながら解いてみてください。
質問はコメント欄からどうぞ。
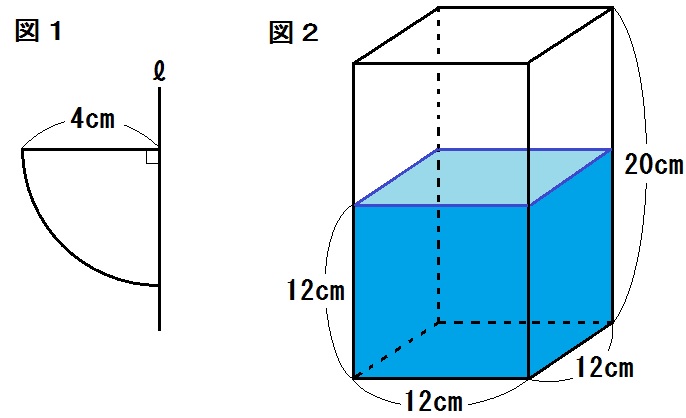
問題1)下の図1の立体の体積を求めよ。
問題2)下の図2の長方形ABCDを、線分ABを回転の軸として1回転させてできる立体の体積は63 \(\pi\) ㎤だった。線分ABの長さを求めよ。
問1)30㎤
問2)7cm
[関連記事]
中学数学「空間図形」② 位置関係・展開図・回転体のコツ
錐の体積

錐ってのは、柱から \( \frac{1}{3}\) だけ削り出してとんがらせた立体。
だから四角柱から \( \frac{1}{3}\) だけ削り出せばピラミッド。円柱から \( \frac{1}{3}\) だけ削り出せばコーンになります。
ここから
$$ \mbox{錐の体積} = \mbox{(柱の体積)} \times \frac{1}{3} $$
つまり
$$ \mbox{錐の体積} = \mbox{(底面積)} \times \mbox{(高さ)} \times \frac{1}{3} $$
という公式が生まれます。
とにかく「錐=とんがった立体」です。
では、応用問題を解いていきましょう。
これも三角錐だ!
例題3のポイントは、「四面体ABCFは三角錐だ!」と気づくかどうか。
つまり、以下3パターンのどれかに気づくかどうかです。
- 底面が△ABC、高さがBF
- 底面が△ABF、高さがBC
- 底面が△BCF、高さがAB
(底面を△ACFにすると高さがわからない)
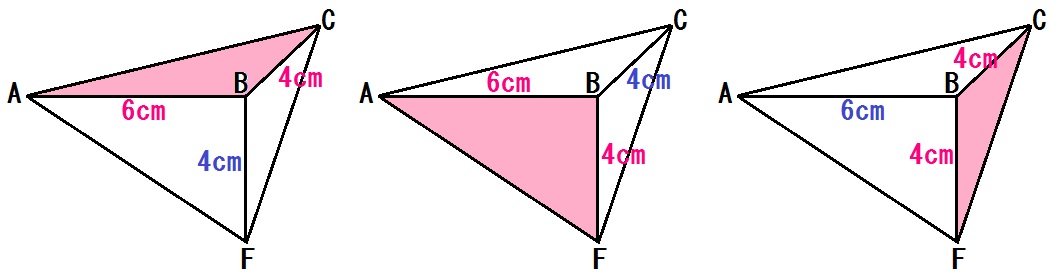
みなさん、錐って「とんがりがまんなかにくる立体だけ」と思い込んでいませんか?
上から見たとき、とんがりがズレてても、それ錐なんです。
よって例題3の求め方は、たとえば底面を△ABCとみると以下のとおり。
\begin{eqnarray} & & 6 \times 4 \times \frac{1}{2} \times 4 \times \frac{1}{3} \\ &=& 16 \end{eqnarray}
答.16㎤
ちなみに式をぜんぶつなげて書くと、最後の \(\frac{1}{3}\) が \(6\) と約分できますね。
これも計算がラクになる一例です。
ってことで、例題3のポイントはとんがりがズレてても錐。
加えて言えば、三角錐は底面&高さの見方が何パターンもあるってことです。
このパターンの多さから、たとえば「Bから面ACFに垂ろした垂線の長さを求めよ」なんて問題も、入試では頻出します。
時間のある方はやってみてください。
*三平方の定理を使うので中3以上の知識が必要です。ちなみに答えは \(\frac{6 \sqrt{22}}{11}\) cm。
[関連記事]
中学数学「平面図形」のコツ③ 作図の高校入試問題を解いてみよう
複雑な形の立体は
例題4のような、複雑な形の立体。
その体積を求めるポイントは、
- 分けて、たす
- 大きく求めて、ひく
のどちらかを使うこと。
例題4の場合、問題文を読めば「円錐と円柱の2つに分けて、たす」でいけるとわかりますね。
よって解答は以下のとおり。
\begin{eqnarray} & & 6 \times 6 \times \pi\times 4 \times \frac{1}{3} \ + \ 6 \times 6 \times \pi \times 5 \\ &=& 48 \pi \ + \ 180 \pi \\ &=& 228 \pi \end{eqnarray}
答.228 \(\pi\) ㎤
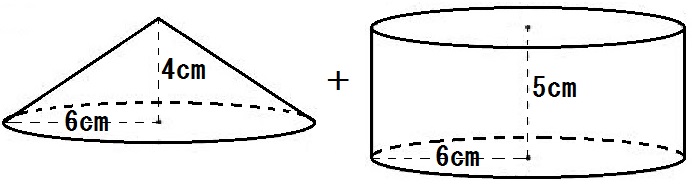
体積にかぎらず、複雑な図形をやっつけるには
- 分けて、たす
- 大きく求めて、ひく
の2通りが使えます。
たとえばグラフ上の三角形の面積を求めるときなど、しょっちゅう使う。ぜひこのコツを覚えて利用してください。
[関連記事]
中学数学「比例と反比例」の教え方⑤ 座標とグラフ
*グラフ上の三角形の面積の求め方は、記事内の「座標の指導案(応用)」の章で解説しています。
練習問題
では錐の体積の練習問題です。
問題3は長崎県の公立高校入試問題。2019年度の大問4の1-3をそのまま載せます。
また問題4は回転体の体積問題をつくってみました。
どちらも応用問題ですので、質問があればコメント欄からいつでもどうぞ。
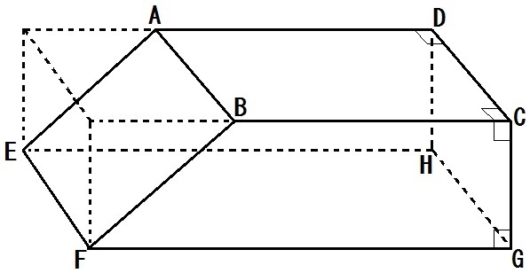
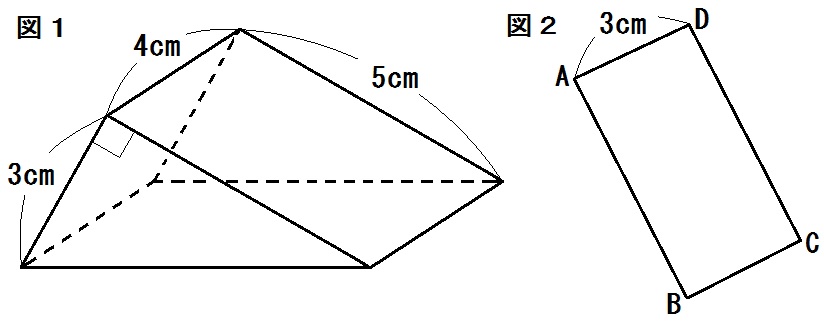
問題3)図1のように三角柱ABCDEFがあり、AB=BC=4cm、AD=8cm、∠ABC=90°である。
- 辺ABとねじれの位置にある辺は全部で何本あるか。
- 三角柱ABCDEFの体積は何㎤か。
- 図2のように、辺BE上に点Pをとる。三角錐ABCPの体積が三角柱ABCDEFの体積の \(\frac{1}{4}\) 倍であるとき、線分BPの長さは何cmか。
問題4)図3の図形を、直線ℓを回転の軸として1回転させてできる立体の体積を求めよ。
問3)1.3本 2.64㎤ 3.6cm
問4)360 \(\pi\) ㎤
[関連記事]
中学数学「空間図形」② 位置関係・展開図・回転体のコツ
球の体積

最後に、球の体積問題を解説します。
球の体積 \(V\) は
$$ V= \frac{4}{3} \pi r^3 $$
という公式で求まります。
この公式がどうやって出てくるかを説明するには高校数学の積分が必要なんで、中学生はもう覚えてしまいましょう。
覚え方は、よく言われるように、以下のごろ合わせです。
「身の上に、心配あ~る、参上する」
[関連記事]
部活動でいま人気なのは何部?ランキングと推移をデータで検証
球の公式の覚え方

ちょっとだけ、どーでもいい小話をします。
あなたが大学生になって、親元を離れ一人暮らしを始めたと想像してください。
たまたまスマホが壊れて、一か月ほど親に連絡しなかったとしましょう。
ある日突然、アパートのドアが開いて、親が訪ねてきます。
「おかーさん!どうしたの?」
「あんた、なんで連絡しないの!」
「スマホが壊れてたんだよ」
「わたしはあなたの身の上が心配で、こうして参上したんだよ」
「そっか、わたしの身の上に心配があるので、参上したんだね」
以上、球の公式を覚えるための小話でした。
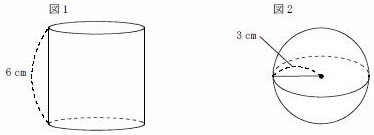
例題5)図1のように、高さが6cmで、底面の直径が高さと等しい円柱と、図2のように、半径3cmの球がある。図1の円柱の体積から、図2の球の体積をひいたときの差を求めなさい。
2019 三重県公立高校入試問題 4-1
閑話休題。
球の公式をつかって、例題5を解きましょう。
\begin{eqnarray} & & 3 \times 3 \times \pi \times 6 \ – \ \frac{4}{3} \pi \times 3 \times 3 \times 3 \\&=& 54 \pi \ – \ 36 \pi \\&=& 18 \pi \end{eqnarray}
答.18 \(\pi\) ㎤
かんたんですね。
ちなみに例題5で、円柱と球の体積は
$$ 54 \pi : 36 \pi = 3:2 $$
となってます。
一般に、球の体積は、その球がすっぽり入る円柱の体積の \(\frac{2}{3}\) となります。
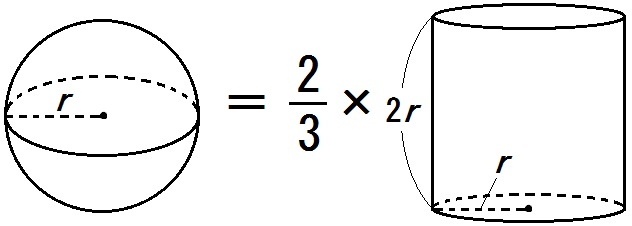
ここから
\begin{eqnarray} \mbox{球の体積} &=& \frac{2}{3} \times \mbox{すっぽりな柱の体積} \\ &=& \frac{2}{3} \times \ r \times r \times \pi \times 2r \\&=& \frac{2}{3} \times 2 \pi r^3 \\ &=& \frac{4}{3} \pi r^3 \end{eqnarray}
と、球の公式を出すこともできます。
「身の上に…」を万一忘れてしまった場合にそなえて、覚えておいてもいいでしょう。
水を入れる問題は
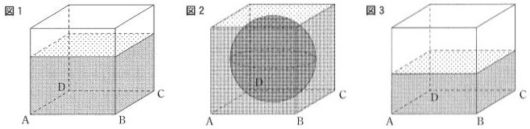
例題6)図1のように、1辺6cmの立方体の形をした透明な容器を、底面ABCDが水平な台の上に接するように置いてから水を入れた。
ここに図2のように、半径3cmの鉄球を容器の底につくまで静かに入れたところ、水があふれた。
水があふれなくなってから、鉄球を容器から静かに取り出したところ、図3のようになった。
このときの底面ABCDから水面までの高さを求めなさい。
ただし、容器の厚さは考えないものとし、また鉄球を取り出すときに容器内の水の量は変化しないものとする。
2019 富山県公立高校入試問題 5-2
最後に、かなり長いですが、水を入れる問題を考えます。
例題6のような水を入れる問題のポイントは、水って形は変わっても体積は変わらないということです。
つまり例題6でいえば、
$$ \mbox{図2の水の体積} = \mbox{図3の水の体積} $$
そして
$$ \mbox{図2の水の体積} = \mbox{1辺6cmの立方体} \ – \ \mbox{半径3cmの鉄球} $$
で求められる。
水の体積は
\begin{eqnarray} & & 6 \times 6 \times 6 \ – \ \frac{4}{3} \pi \times 3 \times 3 \times 3 \\&=& 216 \ – \ 36 \pi \end{eqnarray}
よって、図3の水の体積も \( 216 – 36 \pi\) (㎤) とわかります。
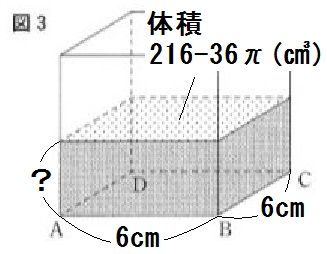
あとは、例題2でもやった高さを求める問題です。
求める高さを \(h\) cmとすると、
\begin{eqnarray} 6 \times 6 \times h &=& 216 – 36 \pi \\ 36h &=& 216 – 36 \pi \\ h &=& 6 – \pi \end{eqnarray}
答.\(6 – \pi\) (cm) と出ます。
以上のように、水を入れる問題のコツは、形は変わっても体積は変わらないという水の特徴を利用することです。
このコツは
$$ \mbox{水の中に入れた立体の体積} = \mbox{押し出された水の体積} $$
という関係で使う場合もあります。(練習問題6がそう)
練習問題
では、最後の練習問題です。
質問はコメント欄からどうぞ。
問題5)下の図1のような図形を、直線ℓを回転軸として1回転させてできる立体の体積を求めよ。
問題6)下の図2のように、水の入った直方体の容器があり、底面は水平である。ここに半径6cmの鉄球を入れたときの、水面の高さを求めよ。また水はこぼれるかどうかも答えよ。ただし容器の厚さは考えず、鉄球を入れたとき水の量は変化しないものとする。
問5)\(\frac{128}{3} \pi\) ㎤
問6)\(12+ 2 \pi\) (cm)、こぼれない
[関連記事]
中学数学「空間図形」② 位置関係・展開図・回転体のコツ
まとめ

空間図形の体積問題で、とくに気をつけるポイントは以下6点。
- 横になってても、柱
- とんがりがズレてても、錐
- 球の体積の公式は「身の上に 心配あ~る 参上する」
- 高さを求める問題などでは、求める長さを文字でおいて方程式をつくる
- 複雑な図形の体積は「分けて、たす」or「大きく求めて、ひく」
- 水って形は変わっても体積は変わらない

以上!
次回は表面積の問題のコツを解説します。
基本となる考え方から、円錐の表面積を深く理解するところまで、ポイントをしぼってお伝えしていきます。
≪「空間図形」の記事一覧≫






コメント
>算数でなく数学ができるようになりたいなら、「未知数を文字でおいて方程式をつくる」という意識を常日頃からもっておくことが大切です。
その通りだと思います。
一方では、「円とおうぎ形」では、「公式を覚える必要ない」として、
「未知数を文字でおいて方程式をつくる」ことなく、答えを求める解法が紹介されています。
(例えば例5)
この両者の関係を、どうとらえたらよいでしょうか?
いいご質問をありがとうございます。
前提として、「未知数を文字でおいて方程式をつくる」という意識は単元に関係なく必要だと私は考えています。
よっておうぎ形であっても、基本を習得した生徒には、公式を使って方程式をつくって解く方法も紹介しています。
ただ「円とおうぎ形」単元では、公式の意味や、おうぎ形が円の一部であることを理解しないままの中1が非常に多いと感じています。
そうした理解をまず促すために、「公式なんて使わなくてもできる」ことを示すのが、円とおうぎ形の記事内容になります。
結果、ご指摘のように、2つの記事で矛盾するような物言いになってしまいました。
「基本が理解・習得できたならおうぎ形の公式を使ってもいい」との一文は加えるべきだったかもしれません。
記事のUPから2年が経ち、さらに指導を重ねた結果、おうぎ形の記事の主張はちょっと極端だったかなと今では思うところもあります。
捕捉です。図が投降した週間に壊れたので気にしないでください。
図がわからないので推測で答えます。
四面体BEGM=四面体BEGCの半分
四面体BEGC=三角柱BEFCHG(直方体の半分)-四面体CHEG-四面体BEFG
三角柱BEFCHG:72
四面体CHEG:24
四面体BEFG:24
よって求める体積は
(72-24-24)÷2=12 12㎤
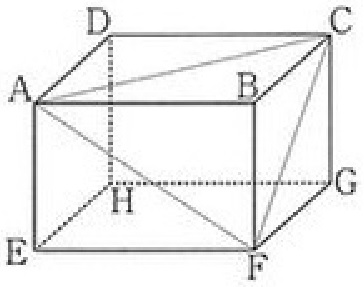
立体ABCD-EFGHはAB=BC=3√2cmAE=8cmの正四角柱である。対角線CEの中点をMとする。
この時、四角形BEGMを求めなさい。
D___________C 四角形BEGM
/| /|
/ | / | B
A/__________/B | /|
| | | | / |
| | | | M |
| | | | | G
| | | | | /
| | | | _________|/
| H|_______|__|G E F
E|__________|F
図が分かりにくくて済みませんが、EHはつながっており、FGもつながっており、GMもつながっており、GEもつながっており、EMもつながっています。
上にある問題がわかりません。解説をお願いしてよろしぃでしょうか?
>算数でなく数学ができるようになりたいなら、「未知数を文字でおいて方程式をつくる」という意識を常日頃からもっておくことが大切です。
その通りだと思います。
一方では、「円とおうぎ形」では、「公式を覚える必要ない」として、
「未知数を文字でおいて方程式をつくる」ことなく、答えを求める解法が紹介されています。
(例えば例5)
この両者の関係を、どうとらえたらよいでしょうか?
>サンダーさま
まず「未知数を文字でおいて方程式をつくる」、これは円とおうぎ形単元でも有効です。
ただ円とおうぎ形単元では、方程式(公式)の意味を理解することなくただ丸暗記して使おうとする、結果として応用問題になると解けないとなる生徒があまりに多い。
そこで、公式が出てくる理由をしっかり理解してもらおうという意味で、あえて「公式を覚える必要はない」と書きました。
つまり、円とおうぎ形単元でつまずく理由とは、生徒が
「未知数を文字でおいて方程式をつくる」という意識ではなく
「公式を丸暗記して問題に当てはめる」という意識になっているから。
そこからの脱却をめざした記事です。
だからもちろん、公式の意味をちゃんと理解したあとだったら、方程式をつくって解く方法でやってもOKです。
(本当はそうした解法も載せる予定でしたが、あまりに記事が長くなったので省略した次第です。ありがとうございます)