三角形の面積を求める公式７選。高校数学のまとめにどうぞ

こんにちはジュウゴです。

先日、大学入試を控えた高校３年生から「三角形の面積の求め方っていくつあるんですか？」と質問を受けました。

その場ではさっと教えましたが、あとになって、そういえば証明もふくめて整理すべき大切な知識だなと反省しました。

そこで反省がてら、三角形の面積を求める公式７つ、ぜんぶまとめます。

• どんな場面でよく使うのか
• 問題を解くときのポイント
• 公式の導出（証明）

という３点を、例題とともに、７つそれぞれで解説します。

高校数学の頭の整理にお役立てください。

1 \(S= \frac{1}{2}ah\)

まずは基本の

$$ \frac{1}{2} \times \mbox{(底辺)} \times \mbox{(高さ)} $$

から。

高校数学ではとくに座標平面の問題でよく使います。

使い方

 

【解答例】

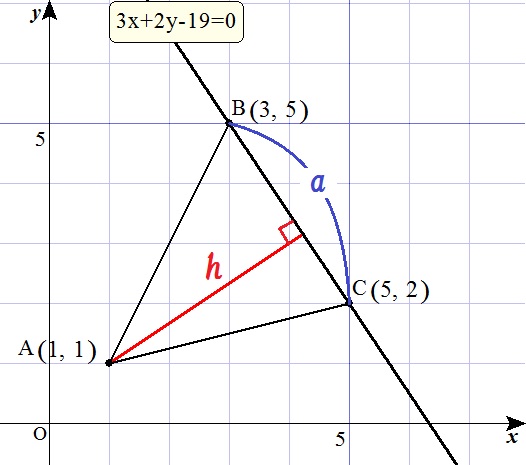
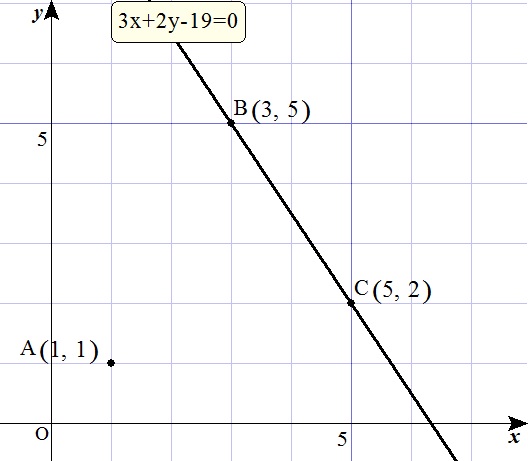
B(3,5)、C(5,2)より

\begin{eqnarray} BC &=& \sqrt{(5-3)^2 + (2-5)^2 } \\ &=& \sqrt{13} \end{eqnarray}

点A(1,1)から直線 \(3x+2y-19=0\) に垂ろした垂線の長さを \(h\) とすると、点と直線の距離より

\begin{eqnarray} h &=& \frac{\vert 3 \cdot 1 + 2 \cdot 1 -19 \vert}{\sqrt{3^2 +2^2}} \\ &=& \frac{14}{\sqrt{13}} \end{eqnarray}

よって

\begin{eqnarray} \mbox{△ABC} &=& \frac{1}{2} \cdot \sqrt{13} \cdot \frac{14}{\sqrt{13}} \\ &=& 7 \end{eqnarray}

答．\(7\)

 

 

公式の証明

こんな感じで、\( \frac{1}{2} ah\) の公式は座標平面でよく登場します。

ここでは数Ⅱ「図形と方程式」単元で習う「点と直線の距離」との合わせワザでしたが、ほかにも「積分」単元で使ったりもします。

では、公式の証明を。

こいつはカンタンですね。

【証明】

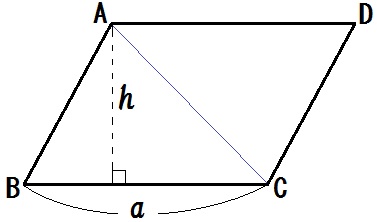
図のような平行四辺形ABCDでBC= \(a\) 、高さ \(h\) とすると

(平行四辺形ABCD) = \( ah \)

△ABC = \( \frac{1}{2} \times \)(平行四辺形ABCD)

よって △ABC = \(\frac{1}{2} ah \)

（証明おわり）

 

2 \(S= \frac{1}{2}bc \sin A\)

つぎに、数Ⅰ三角比から

$$ \frac{1}{2} \times \mbox{(はさむ辺)} \times \mbox{(はさむ辺)} \times \mbox{(はさまれた角のサイン)}$$

です。

記号で書くと３通りになりますが、ジュウゴは↑のようなイメージで教えています。

使う場面は

• 二辺とその間の角度がわかっている
• 三辺の長さがわかっている

ときなどです。

使い方

 

【解答例】

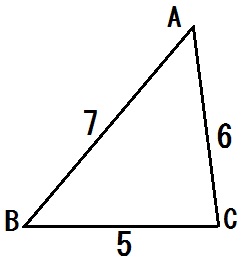
余弦定理より

\begin{eqnarray} \cos A &=& \frac{6^2 + 7^2 – 5^2}{2 \cdot 6\cdot 7} \\ &=& \frac{60}{2 \cdot 6\cdot 7} \\ &=& \frac{5}{7} \end{eqnarray}

0°＜A＜180°から \( \sin A \) ＞0、
三角比の相互関係より

\begin{eqnarray} \sin A &=& \sqrt{1- \left( \frac{5}{7} \right) ^2} \\ &=& \sqrt{ \frac{24}{7^2} } \\ &=& \frac{2 \sqrt{6}}{7} \end{eqnarray}

よって

\begin{eqnarray} \mbox{△ABC} &=& \frac{1}{2} \cdot 6 \cdot 7 \cdot \frac{2 \sqrt{6}}{7} \\ &=& 6 \sqrt{6} \end{eqnarray}

答．\(6 \sqrt{6} \)

 

公式の証明

このように、三辺がわかっている三角形の面積を求める場合などで、\(S= \frac{1}{2} bc \sin A\) は活躍します。

もちろん、30°や45°などの角度が与えられている問題は言わずもがな。

応用範囲はかなり広い公式です。

では、証明をどうぞ。

【証明】

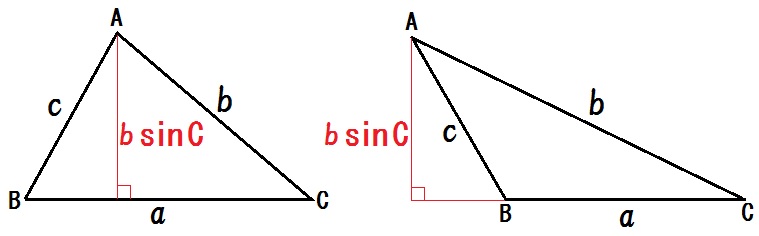
図のような△ABCにおいて
底辺を \(a\) とした場合、
高さはどちらも三角比の定義より

$$ b \sin C $$

となる。

よって

\begin{eqnarray} \mbox{△ABC} &=& \frac{1}{2} \cdot a \cdot b \sin C \\ &=& \frac{1}{2} ab \sin C \end{eqnarray}

\(\frac{1}{2} bc \sin A \) , \(\frac{1}{2} ca \sin B \) についても同様。

（証明おわり）

＞Amazonプライム・ビデオ「人間の証明」

 

3 \(S= \sqrt{s(s-a)(s-b)(s-c)} \)

３番目はいわゆる「ヘロンの公式」です。

三辺の長さがわかっている場合、ヘロンの公式のほうをよく使うという高校生も多いかも。

ただ、

$$ 2s= a+b+c $$

がかんたんな値になるときだけ使うってことに注意しましょう。

使い方

【解答例】

\(2s=5+6+7\) とすると

\(s=9\)

よってヘロンの公式より

\begin{eqnarray} \mbox{△ABC} &=& \sqrt{9 \cdot (9-5) \cdot (9-6) \cdot (9-7)} \\ &=& \sqrt{9 \cdot 4 \cdot 3 \cdot 2} \\ &=& 6 \sqrt{6} \end{eqnarray}

答．\(6 \sqrt{6} \)

 

公式の証明

例題２は \(s=9\) とかんたんな値になったので、ヘロンさんでOKでした。

でも例えば

だったらどうでしょう？

\(s= \frac{11+ \sqrt{7}}{2}\) になって計算たいへんです。

だからヘロンの公式を使うかどうかは、\(s\) を求めてみてから判断する。

計算がどえらいことになりそうだったら他の公式でいく。

こういう整理をしておきましょう。

あと、ヘロンの公式には頭に \(\frac{1}{2}\) が付きません。あわせて注意しましょう。

では、ちょっと長いですが証明をどうぞ。

【証明】

△ABCにおいて、余弦定理より

$$ \cos A = \frac{b^2 +c^2 -a^2}{2bc} $$

\( \sin A\) ＞0より

\begin{eqnarray} \sin A &=& \sqrt{1- \left( \frac{b^2 + c^2 -a^2}{2bc} \right) ^2} \\ &=& \sqrt{ \frac{(2bc)^2 – (b^2 +c^2 -a^2)^2}{(2bc)^2}} \\ &=& \frac{1}{2bc} \sqrt{ \{2bc + (b^2 +c^2 -a^2) \} \{2bc – (b^2 +c^2 -a^2) \}} \\ &=& \frac{1}{2bc} \sqrt{ \{(b+c)^2 – a^2 \} \{a^2 – (b-c)^2 \}} \\ &=& \frac{1}{2bc} \sqrt{(b+c+a)(b+c-a)(a+b-c)(a-b+c)} \quad \mbox{…①} \end{eqnarray}

ここで \(a+b+c=2s\) とすると

\begin{eqnarray} b+c-a&=& 2s-2a = 2(s-a) \\ a+b-c&=& 2s-2c = 2(s-c) \\ a-b+c&=& 2s-2b = 2(s-b) \end{eqnarray}

よって①は

\begin{eqnarray} & & \frac{1}{2bc} \sqrt{2s \cdot 2(s-a) \cdot 2(s-c) \cdot 2(s-b)} \\ &=& \frac{2}{bc} \sqrt{s(s-a)(s-b)(s-c)} \end{eqnarray}

したがって、\(S= \frac{1}{2}bc \sin A\) より

\begin{eqnarray} S &=& \frac{1}{2} bc \cdot \frac{2}{bc} \sqrt{s(s-a)(s-b)(s-c)} \\ &=& \sqrt{s(s-a)(s-b)(s-c)} \end{eqnarray}

（証明おわり）

 

4 \(S= \frac{1}{2}r(a+b+c) \)

三角形の公式、４つめは

$$ \frac{1}{2} \times \mbox{(内接円の半径)} \times \mbox{(三辺の長さの和)} $$

です。

この公式は三角形の面積を求めるよりも内接円の半径を求める問題でよく使います。

使い方

【解答例】

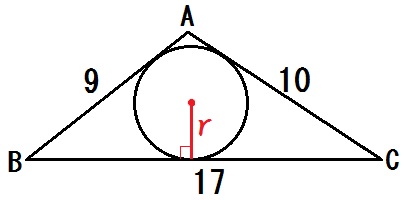
\(2s=17+10+9\) とすると

\(s=18\)

よってヘロンの公式より、△ABCの面積を \(S\) とすると

\begin{eqnarray} S &=& \sqrt{18 \cdot 1 \cdot 8 \cdot 9} \\ &=& 36 \end{eqnarray}

したがって、\(S= \frac{1}{2}r(a+b+c)\) より

\begin{eqnarray} 36 &=& \frac{1}{2} r (17+10+9) \\ 36 &=& 18r \\ r &=& 2 \end{eqnarray}

答．\(2\)

 

公式の証明

このように、三角形の内接円の半径を求める問題で、公式 \(S= \frac{1}{2}r(a+b+c)\) が大活躍します。

「内接円の半径」ときたら、ほぼこの公式一択といってもいいでしょう。

なお、解答例ではヘロンの公式で面積を出しましたが、もちろんサインの公式で出してもOKです。

では、公式の証明をどうぞ。

この公式に関しては特に成り立ちからちゃんと知っておきましょう。

【証明】

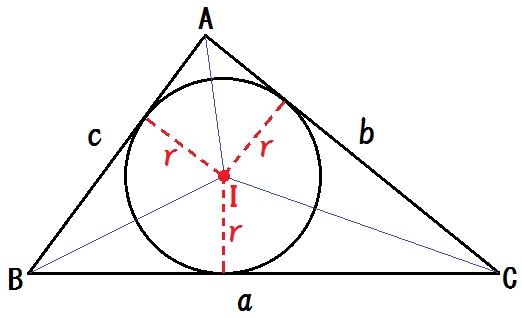
図のように△ABCの内接円の中心をI、半径を \(r\) とする。

$$ \mbox{△ABC} = \mbox{△IBC} + \mbox{△ICA} + \mbox{△IAB} $$

なので、

\begin{eqnarray} \mbox{△ABC} &=& \frac{1}{2}ar + \frac{1}{2}br + \frac{1}{2}cr \\ &=& \frac{1}{2} r(a+b+c) \end{eqnarray}

（証明おわり）

＞Amazonプライム・ビデオ「(r)adius ラディウス(字幕版)」

 

5 \(S= \frac{abc}{4R}\)

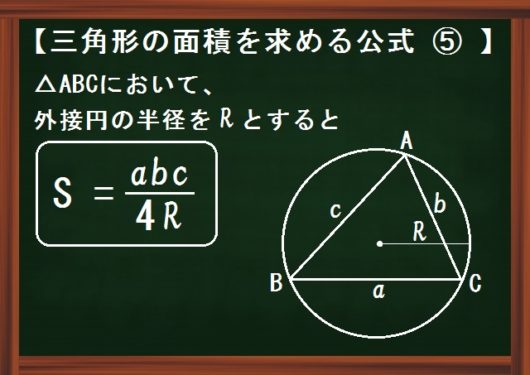
内接円の半径が出てきたので、ついでに外接円の半径を使った公式も紹介します。

$$\frac{\mbox{(三辺の積)}}{4 \times \mbox{(外接円の半径)}}$$

というやつです。

やっぱりというか、外接円の半径を求めるときに使います。

使い方

【解答例】

\(2s=17+10+9\) とすると

\(s=18\)

よってヘロンの公式より、△ABCの面積を \(S\) とすると

\begin{eqnarray} S &=& \sqrt{18 \cdot 1 \cdot 8 \cdot 9} \\ &=& 36 \end{eqnarray}

したがって、\(S= \frac{abc}{4R}\) より

\begin{eqnarray} 36 &=& \frac{17 \cdot 10 \cdot 9}{4R} \\ R &=& \frac{1}{4} \cdot \frac{17 \cdot 10 \cdot 9}{36} \\ R &=& \frac{85}{8} \end{eqnarray}

答．\(\frac{85}{8}\)

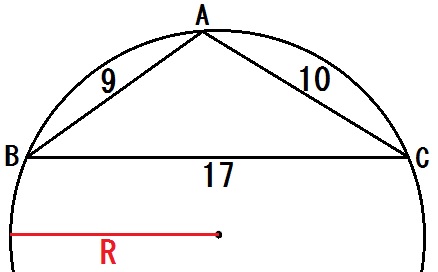
【別解】

余弦定理より

\begin{eqnarray} \cos A &=& \frac{10^2 + 9^2 – 17^2}{2 \cdot 10 \cdot 9} \\ &=& – \frac{3}{5} \end{eqnarray}

0°＜A＜180°から \( \sin A \) ＞0、よって

\begin{eqnarray} \sin A &=& \sqrt{1- \left(- \frac{3}{5} \right) ^2} \\ &=& \frac{4}{5} \end{eqnarray}

正弦定理 \( \frac{a}{\sin A} =2R\) より

\begin{eqnarray} R &=& \frac{1}{2} \cdot \frac{a}{\sin A} \\ &=& \frac{1}{2} \cdot \frac{17}{\frac{4}{5}} \\ &=& \frac{85}{8} \end{eqnarray}

答．\(\frac{85}{8}\)

 

公式の証明

このように、三角形の外接円の半径を求めるには \(S= \frac{abc}{4R}\) か正弦定理を使います。

正弦定理で求まっちゃうので、正直、あまり使うことはないかもしれません。

いちおう知っておくくらいでいいでしょう。

では、証明をどうぞ。

【証明】

△ABCにおいて正弦定理より

\begin{eqnarray} \frac{a}{\sin A} &=& 2R \\ \sin A &=& \frac{a}{2R} \end{eqnarray}

よって

\begin{eqnarray} \mbox{△ABC} &=& \frac{1}{2} bc \sin A \\&=& \frac{1}{2} bc \cdot \frac{a}{2R} \\&=& \frac{abc}{4R} \end{eqnarray}

（証明おわり）

 

6 \(S= \frac{1}{2} \sqrt{ \vert \vec{ a } \vert ^2 \vert \vec{ b } \vert ^2 – (\vec{ a } \cdot \vec{ b })^2 } \)

三角形の面積６つめは、ベクトルの公式です。

とくにベクトルの成分がわかっているときによく使います。

使い方

【解答例】

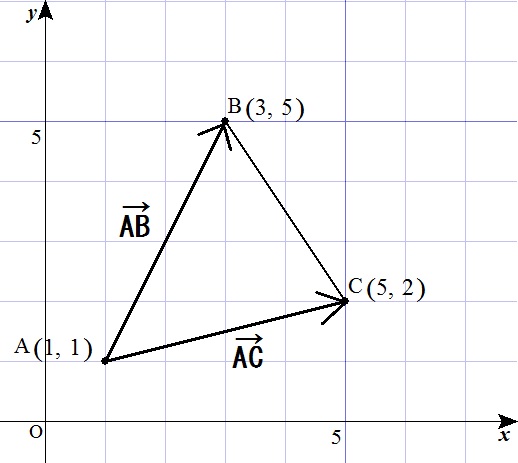
\(\vec{AB} =(2,4)\) , \(\vec{AC} =(4,1)\) より

\( \vert \vec{ AB } \vert = \sqrt{2^2 + 4^2} = 2 \sqrt{5} \)

\( \vert \vec{ AC } \vert = \sqrt{4^2 + 1^2} = \sqrt{17} \)

\( \vec{ AB } \cdot \vec{ AC } = 2 \times 4 + 4 \times 1 = 12 \)

よって

\begin{eqnarray} \mbox{△ABC} &=& \frac{1}{2} \sqrt{(2 \sqrt{5})^2 (\sqrt{17})^2 – 12^2 } \\&=& \frac{1}{2} \sqrt{20 \cdot 17 – 144} \\&=& \frac{1}{2} \cdot 14 \\&=& 7 \end{eqnarray}

答．\(7\)

 

公式の証明

このように、２つのベクトルの大きさおよびその内積がわかってたら、この公式が使えます。

成分表示の場合にはそれら全部がすぐわかるんで、よく使用するというわけです。

平面・空間にかかわらず、ベクトル成分や座標が表示されてる問題で「三角形の面積」とか出てきたら、この公式が使えないかなーと疑うといいでしょう。

では、公式を証明します。

【証明】

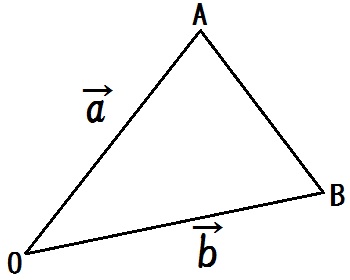
図のような△OABで、\(\vec{OA} = \vec{a}\) , \(\vec{OB} = \vec{b}\) とする。

\begin{eqnarray} \mbox{△ABC} &=& \frac{1}{2} \vert \vec{a}\vert \vert \vec{b} \vert \sin \angle AOB \\ &=& \frac{1}{2} \vert \vec{a}\vert \vert \vec{b} \vert \sqrt{1 – \cos^2 \angle AOB} \\ &=& \frac{1}{2} \vert \vec{a}\vert \vert \vec{b} \vert \sqrt{1 – \left( \frac{\vec{a} \cdot \vec{b}}{\vert \vec{a}\vert \vert \vec{b} \vert} \right)^2 } \\ &=& \frac{1}{2} \vert \vec{a}\vert \vert \vec{b} \vert \sqrt{\frac{(\vert \vec{a}\vert \vert \vec{b} \vert)^2 -(\vec{a} \cdot \vec{b})^2}{(\vert \vec{a}\vert \vert \vec{b} \vert)^2}} \\ &=& \frac{1}{2} \sqrt{\vert \vec{a}\vert^2 \vert \vec{b} \vert^2 – (\vec{a} \cdot \vec{b})^2} \end{eqnarray}

（証明おわり）

[関連記事]
三角比とはなんだ？何の役に立つ？どんな歴史があるの？

 

7 \(S= \frac{1}{2} \vert x_1 y_2 – x_2 y_1 \vert \)

三角形の公式、ラストも座標のやつで、

$$ \frac{1}{2} \vert \mbox{外・外} – \mbox{内・内} \vert$$

という感じです。

この公式は三角形の頂点のうち１つが原点にないと使えません。

よって、頂点の１つが原点にくるように平行移動させて使います。

使い方

【解答例】

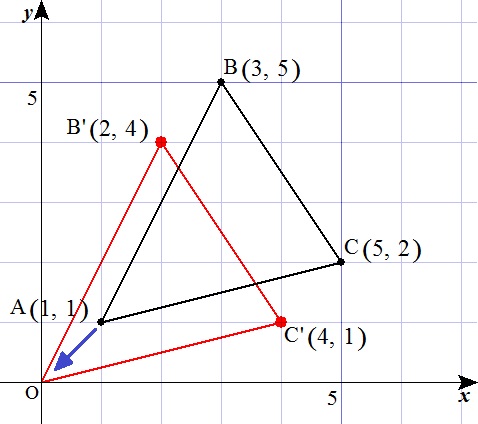
頂点Aが原点Oにくるように△ABCを平行移動すると、

\(O(0,0)\) , \(B'(2,4)\) , \(C'(4.1)\) 。

よって

\begin{eqnarray} \mbox{△ABC} &=& \mbox{△OB’C’} \\ &=& \frac{1}{2} \vert 2 \cdot 1 – 4 \cdot 4 \vert \\ &=& \frac{1}{2} \cdot \vert -14 \vert \\ &=& 7 \end{eqnarray}

答．\(7\)

 

公式の証明

このように、頂点のひとつをムリヤリ原点にもってきて、公式を使うことができます。

３点の座標がわかってる三角形の面積の求め方は

$$ S= \frac{1}{2}ah $$

$$ S= \frac{1}{2} \sqrt{ \vert \vec{ a } \vert ^2 \vert \vec{ b } \vert ^2 – (\vec{ a } \cdot \vec{ b })^2 } $$

$$ S= \frac{1}{2} \vert x_1 y_2 – x_2 y_1 \vert $$

という３つがありましたが、このラストの公式が計算はいちばんラクかも。

では、最後の公式の証明です。

方法はいろいろありますが、せっかくなんで公式６から導出します。

【証明】

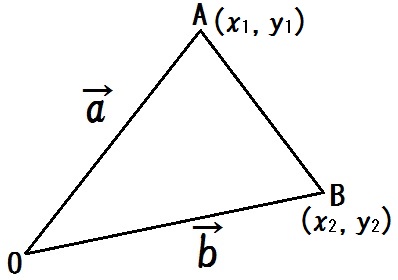
図のような△OABで、\(\vec{OA} = \vec{a}\) , \(\vec{OB} = \vec{b}\) 、

また \(A(x_1 , y_1)\) , \(B(x_2 , y_2)\) とする。

\begin{eqnarray} & & \vert \vec{a}\vert^2 \vert \vec{b} \vert^2 – (\vec{a} \cdot \vec{b})^2 \\ &=& (x_1 ^2 + y_1 ^2)(x_2 ^2 + y_2 ^2) – (x_1 x_2 + y_1 y_2)^2 \\ &=& x_1 ^2 y_2 ^2 + x_2 ^2 y_1 ^2 – 2 x_1 x_2 y_1 y_2 \\ &=& (x_1 y_2 – x_2 y_1)^2 \end{eqnarray}

よって

\begin{eqnarray} \mbox{△ABC} &=& \frac{1}{2} \sqrt{ \vert \vec{a}\vert^2 \vert \vec{b} \vert^2 – (\vec{a} \cdot \vec{b})^2 } \\ &=& \frac{1}{2} \sqrt{ (x_1 y_2 – x_2 y_1)^2 } \\ &=& \frac{1}{2} \vert x_1 y_2 – x_2 y_1 \vert \end{eqnarray}

（証明おわり）

[関連記事]
数学の証明ってなに？なんで証明するの？なぜ文字を使うの？

 

まとめ

以上、三角形の面積を求める公式７つでした。

ご意見・ご感想などお待ちしています。