中学数学「多項式」の教え方④ 因数分解

中３数学「多項式」の４回目。

今回から因数分解のやり方に入ります。

• 例1-1）\(6x^2 -15x\)
• 例2-1）\(x^2 -16\)
• 例3-1）\(x^2 +6x+9\)
• 例4-1）\(x^2 -16xy+64y^2\)
• 例5-1）\(x^2 +8x+15\)
• 例6-1）\(x^2 +9xy+14y^2\)

因数分解で生徒がとくに「わからない・できない・むずかしい」となるのは例３～例６の問題。

つまり公式２・公式１を使った因数分解の問題です。

そこで、公式を使った因数分解を教える際は、公式３→公式２→公式１という指導順がおススメです。

またそれぞれの学習に入るときには、中学生がつまずかないための準備をしてあげるといいでしょう。

準備といっても特別なものじゃありません。

この記事を読めばすぐに実践できるので、ぜひ教室でも家庭でもご活用ください。

では、因数分解のわかりやすいやり方を見ていきましょー。

共通因数でくくる

因数分解のはじめは、共通因数でくくる問題です。

ここでの準備は「因数分解とは何か」をわかりやすく説明してあげること。

以下、指導例をどうぞ。

準備：因数分解とは何か

これから因数分解という内容に入る。

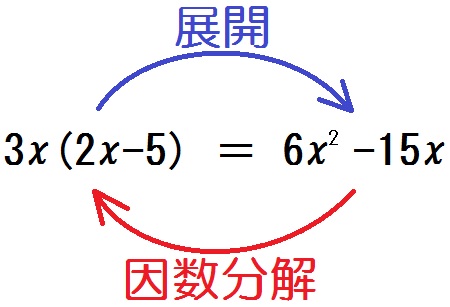
因数分解とは、展開の逆のこと。

たとえば以下の式を展開するとこうだった。

\begin{eqnarray} & & 3x(2x-5) \\ &=& 6x^2 -15x \end{eqnarray}

でも因数分解では、問題と答えが逆になる。

\begin{eqnarray} & & 6x^2 -15x \\ &=& 3x(2x-5) \end{eqnarray}

つまり

• 展開：カッコのある式をカッコのない式にすること
• 因数分解：カッコのない式をカッコのある式にすること

こういう計算を、これからやっていきます。

 

因数分解のやり方

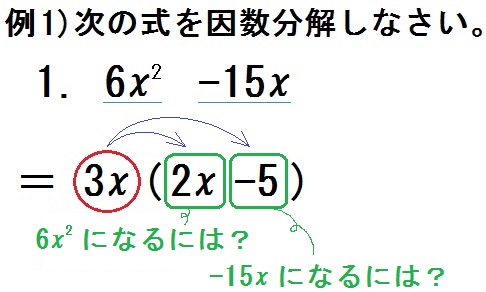
では、\(6x^2 -15x\) という式をみて \(3x(2x-5) \) と答えるにはどうやればいいか？

ポイントは、カッコの前の \(3x\) 。

どうやって見つけるかというと、問題式を項ごとに分けて、共通している部分をぬきだすんだ。

つまり、
\(3\) ← 6と15の最大公約数
\(x\) ← 共通している文字
ってこと。

この \(3x\) みたいに、各項に共通しているもの全部を共通因数と呼びます。

共通因数をくくり出したら、あとはカッコの中身を考えればいい。

カッコの中身は、展開して元に戻るには？と考えること。

\(3x\) とかけて \(6x^2\) になるには？
→ \(2x\)

\(3x\) とかけて \(-15x\) になるには？
→ \(-5\)

 

やり方はわかったね。

じゃ例1-2と例1-3もやってみよう。

共通因数はなに？
→ \(x\)

じゃ \( x( \qquad ) \) は決まり。
あとは元に戻るようにカッコの中身を考えて？
→ \(x(y-9) \)

\begin{eqnarray} & & xy-9x \\ &=& x(y-9) \end{eqnarray}

このように共通因数が文字だけのこともある。

 

共通因数はなに？
→ \(4\)

じゃ \( 4( \qquad ) \) は決まり。
あとは元に戻るようにカッコの中身を考えて？
→ \(4(2a+3b+5c) \)

\begin{eqnarray} & & 8a+12b+20c \\ &=& 4(2a+3b+5c) \end{eqnarray}

このように共通因数が数字だけになることもある。

なお、共通因数は \(2\) ではない。

共通しているもの全部が共通因数だから、4,8,12の最大公約数 \(4\) をくくり出すんだ。

まちがいやすいから気をつけて。

 

注意点と練習問題

以上が共通因数でくくる問題の教え方です。

ジュウゴがここの指導で注意しているのは、正確なことばづかいにこだわりすぎないことです。

• 「因数分解とは、多項式をいくつかの単項式または多項式の積の形で表すこと」
• 「共通因数とは、各項に共通してかけられている数字や文字のこと」
• 「そもそも因数とは、積の要素のこと」…。

こんな説明されても、中学生はポカンとします。

じつはわたしも過去にこんな説明をして、中３生たちの頭をクエスチョンマークだらけにしたことがありました。

言葉であれこれ言うよりも、じっさいにやってみせる。

よっぽど国語力のある生徒でないかぎり、そのほうがいいでしょう。

＞Amazonプライム・ビデオ「センセイの鞄」

 

では例題を終えたら、問題を一緒にやって、させてみて、「わかる」を「できる」にしてあげてください。

展開をしっかり練習していれば因数分解の練習はそこまで必要ないので、おすすめサイトをひとつ掲載して代わりとします。

「中学校数学学習サイト」というサイトのなかの練習問題ページです。

印刷もかんたんにできるみたいですよ。

○因数分解(共通因数1)

○因数分解(共通因数2)

 

公式３を使った因数分解

次に、公式３を使った因数分解です。

ここでの準備は、二乗した数に慣れること。

以下、指導例をどうぞ。

準備：二乗した数に慣れる

次に、例題２をやってみよう。

問題をじっくり見たら、共通因数はないことに気づくね。

ではどうやればいいか？

ここで、展開の公式（乗法公式）の３つめを思い出してくれ。

$$ (x+4)(x-4)= x^2 -16 $$

これの逆をやればいいんだ！

つまり
\(x^2\) ← \(x\) の二乗
\(16\) ← \(4\) の二乗
と気づいたら

$$ a^2 -b^2 = (a+b)(a-b) $$

に当てはめて

$$ x^2 -16 = (x+4)(x-4) $$

とやればいい。

これが因数分解の方法その２。

ただこの方法を使うには、問題を見たときに「～を二乗したやつだ！」と気づく必要がある。

そこでちょっと二乗した数に慣れておこう。

以下の数字や文字が何を二乗したものか、答えて。

\begin{eqnarray} & & 16 \quad 25 \quad 81 \quad 36 \quad 100 \\ & & 4 \quad 49 \quad 9 \quad 64 \quad 1 \\ & & 121 \quad 144 \quad 169 \quad 196 \quad 225 \\ & & 256 \quad 289 \quad 324 \quad 361 \\ & & \frac{1}{4} \quad \frac{1}{9} \quad \frac{16}{25} \quad \frac{49}{100} \quad \frac{121}{36} \\ & & x^2 \quad 4x^2 \quad 9y^2 \quad 16a^2 \quad \frac{1}{4}b^2 \\ & & x^2 y^2 \quad y^2 z^2 \quad a^2 b^2 \quad 36x^2 y^2 \quad 9x^2 y^2 z^2 \end{eqnarray}

 

因数分解のやり方

よし、準備は完了。

例題２を一緒にやってみよう。

\(x^2\) は何の二乗？→ \(x\)
\(16\) は何の二乗？→ \(4\)
よって、

\begin{eqnarray} & & x^2 -16 \\ &=& (x+4)(x-4) \end{eqnarray}

 

\(4x^2\) は何の二乗？→ \(2x\)
\(81\) は何の二乗？→ \(9\)
よって、

\begin{eqnarray} & & 4x^2 -81 \\ &=& (2x+9)(2x-9) \end{eqnarray}

 

\(36x^2\) は何の二乗？→ \(6x\)
\(y^2 z^2\) は何の二乗？→ \(yz\)
よって、

\begin{eqnarray} & & 36x^2 -y^2 z^2 \\ &=& (6x+yz)(6x-yz) \end{eqnarray}

よくできた！

 

注意点と練習問題

公式３を使った因数分解で注意することはおもに２つです。

１つ。
はじめに「この問題に共通因数はない」と確認すること。

次回の記事でくわしく解説しますが、共通因数があれば共通因数でくくる、これは因数分解においていちばん最初にやる手順です。

その手順をすこしずつ身につけるためにも、問題の式に共通因数がないか必ず確認しましょう。

これは公式２・公式１でも同様です。

 

２つ。
二乗に慣れる練習では、11以上の数字・分数・文字２つもやっておくといい。

つまり

• \(121\) （11の二乗）
• \(\frac{1}{4}\) （２分の１の二乗）
• \(x^2 y^2\) （xyの二乗）

なども練習するといい。

なぜなら問題で出るからです。

ちなみにジュウゴはこの段階で11～19の二乗も覚えさせます。

そうすることで、次単元の平方根でも、たとえば \( \sqrt{289} \) が簡単に外せるようになるからです。

 

では、公式３を使った因数分解の練習をどうぞ。

リンク先は「因数分解(公式2)」となってますが、大問３が公式３を使った因数分解になってます。

○因数分解(公式2)

 

つづいて公式２と公式１を使った因数分解を解説します。

＞次ページ：公式２・公式１を使った因数分解