中学数学「多項式」の教え方④ 因数分解

つづいて公式２・公式１を使った因数分解です。

このページから開いちゃった人は、まず前ページを読んでください。

＞前ページ：共通因数でくくる・公式３を使った因数分解

公式２を使った因数分解
公式１を使った因数分解
まとめ

公式２を使った因数分解

指導順の３番目、公式２を使った因数分解。

ここでの準備は「前・うしろかけて２倍」を練習することです。

以下、指導例をどうぞ。

準備：前うしろかけて２倍

では次に、こんな問題をやってみよう。

例題３）次の式を因数分解しなさい。

$x^2 +6x+9$
$x^2 -14x+49$
$x^2 +22x+121$

この問題にも共通因数はない。

また $x^2 -16$ みたいな問題ともちがう。項が３つあるもんね。

ではどうやればいいか？

ここで、展開の公式（乗法公式）の２つめを思い出してくれ。

$$ (x+3)^2 = x^2 +6x+9 $$

この逆をやればいいんだ！

つまり
$x^2$ ← $x$ の二乗
$9$ ← $+3$ or $-3$ の二乗
$+6x$ ← $x \times +3$ の２倍
となってたら

$$ a^2 +2ab+b^2 = (a+b)^2 $$

に当てはめて

$$ x^2 +6x+9 = (x+3)^2 $$

とやればいい。

これが因数分解の方法その３。

ただこの方法を使うには、二乗した数に慣れてて、かつ「前・うしろかけて２倍」の計算も暗算でできないとむずかしい。

そこでやはり練習しよう。

以下の数字や文字を「かけて２倍」したもの、暗算で答えて。

\begin{eqnarray} & & x \mbox{と} +2 \quad x \mbox{と} -8 \quad x \mbox{と} +5 \\ & & x \mbox{と} -7 \quad x \mbox{と} +6 \quad x \mbox{と} -1 \\ & & x \mbox{と} +11 \quad x \mbox{と} -13 \quad x \mbox{と} +14 \\ & & x \mbox{と} -4y \quad x \mbox{と} +9y \quad x \mbox{と} -10y \\ & & 2x \mbox{と} +3 \quad 3x \mbox{と} -1 \quad 4x \mbox{と} +5 \\ & & 5x \mbox{と} -4y \quad 3x \mbox{と} +4y \quad 2x \mbox{と} -6y \end{eqnarray}

因数分解のやり方

よし、準備は完了。

例題３を一緒にやってみよう。

$$ \mbox{例3-1）} \ x^2 +6x+9 $$

前は何の二乗？→ $x$
うしろは何の二乗？→ $+3$ or $-3$
前うしろかけて２倍すると $+6x$ になるのは、$+3$ のほうだ。
よって、

\begin{eqnarray} & & x^2 +6x+9 \\ &=& (x+3)^2 \end{eqnarray}

よくできた！

ここで気づいたと思うけど、
$ x^2 +6x+9 = (x+3)^2 $
$ x^2 -6x+9 = (x-3)^2 $
だから、
カッコ内の符号は問題式のまんなかの項と同じになる。

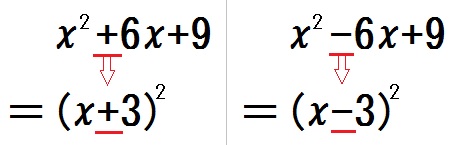
これを使って、以下、もっとカンタンにやってみよう。

$$ \mbox{例3-2）} \ x^2 -14x+49 $$

前は何の二乗？→ $x$
うしろは何の二乗→ $7$
前うしろかけて２倍→ $14x$
あとは符号に気をつけて、

\begin{eqnarray} & & x^2 -14x+49 \\ &=& (x-7)^2 \end{eqnarray}

$$ \mbox{例3-3）} \ x^2 +22x+121 $$

前は何の二乗？→ $x$
うしろは何の二乗→ $11$
前うしろかけて２倍→ $22x$
あとは符号に気をつけて、

\begin{eqnarray} & & x^2 +22x+121 \\ &=& (x+11)^2 \end{eqnarray}

ここまできたら、例題４もできるね。

一気にやってみよう。

例題４）次の式を因数分解しなさい。

$x^2 -16xy+64y^2$
$4x^2 +12x+9$
$25x^2 -40xy+16y^2$

\begin{eqnarray} \mbox{例4-1）}& & x^2 -16xy+64y^2 \\ &=& (x-8y)^2 \\ \mbox{例4-2）}& & 4x^2 +12x+9 \\ &=& (2x+3)^2 \\ \mbox{例4-3）}& & 25x^2 -40xy+16y^2 \\ &=& (5x-4y)^2 \end{eqnarray}

よくできた！

あとは問題をたくさんやって「わかる」を「できる」にしていこう。

くもんの中学基礎がため100％中3数学　〔2012〕改訂新版計算・関数編【合計3000円以上で送料無料】

posted with カエレバ

楽天市場

Amazon

注意点と練習問題

ここの因数分解は、計算力の低い子を中心に苦手とする中学生が多くなります。

しかし、上記のような「前うしろかけて２倍」という準備をすれば難しくありません。

とくに「$2x$ と $+3$」のような練習もしていれば、例題４もスムーズにのりこえていけます。

ぜひ、実際の問題にいく前に、上記の準備練習をさせてください。

ちなみに生徒のなかには、
「前もうしろも何かの二乗だったら、まんなかが『前うしろかけて２倍』っていう確認はいらないんじゃない？」という人もいるでしょう。

そんな中学生には以下の問題を出して、この式が因数分解できるか聞いてみてください。

$$ x^2 -3x+9 $$

そしてこの問題を $ (x-3)^2 $ と答えた生徒には、「まんなかが前うしろかけて２倍になってないからバツ。この問題は因数分解できない」と教えてあげてください。

この確認は高校数学にもつながりますね。

数Ⅰでこんな因数分解を習いますもんね↓

\begin{eqnarray} & & x^3 +27 \\ &=& (x+3)(x^2 -3x +9) \end{eqnarray}

では例によって「中学校数学学習サイト」様より、練習問題をどうぞ。

○因数分解(公式2)

公式１を使った因数分解

さいごは公式１を使った因数分解です。

ここでの準備は「足していくら、かけていくら」を練習すること。

以下、指導例をどうぞ。

準備：足して？かけて？

次はこんな問題をやってみよう。

例題５）次の式を因数分解しなさい。

$x^2 +8x+15$
$x^2 -5x+4$
$x^2 +4x-12$

この例題５にも共通因数はない。

また、$ a^2 -b^2 = (a+b)(a-b) $ も使えない。

そして、$ a^2 +2ab+b^2 = (a+b)^2 $ もよく見たら当てはまらない。

じゃどうすればいいか？

ここで、展開の公式（乗法公式）の１つめを思い出そう。

$$ (x+5)(x+3)= x^2 +8x+15 $$

これの逆をやればいいんだ！

つまり
$+8$ ← $+5$ + $+3$
$+15$ ← $+5$ × $+3$
になってるから

$$ x^2 +(a+b)x +ab = (x+a)(x+b) $$

に当てはめて

$$ x^2 +8x+15 = (x+5)(x+3) $$

とやればいい。

これが因数分解の方法のラスト。

ただこの方法を使うには、「足して $+8$ 、かけて $+15$ 」になる２数をパッと思いつかなきゃいけない。

そこでここでも練習しておこう。

以下の２数、足していくら・かけていくらを暗算で答えて。

\begin{eqnarray} & & +2 \mbox{と} +4 \quad +6 \mbox{と} +2 \quad +2 \mbox{と} +9 \\ & & +3 \mbox{と} +1 \quad +4 \mbox{と} +3 \quad +3 \mbox{と} +8 \\ & & -4 \mbox{と} -5 \quad -7 \mbox{と} -4 \quad -5 \mbox{と} -2 \\ & & -6 \mbox{と} -5 \quad -7 \mbox{と} -1 \quad -8 \mbox{と} -9 \\ & & +4 \mbox{と} -2 \quad +6 \mbox{と} -3 \quad +8 \mbox{と} -4 \\ & & -8 \mbox{と} +6 \quad -9 \mbox{と} +1 \quad -10 \mbox{と} +9 \end{eqnarray}

因数分解のやり方

準備は完了。

例題５を一緒にやってみよう。

$$ \mbox{例5-1）} \ x^2 +8x+15 $$

足して $+8$ 、かけて $+15$ になる２数は？
→ $+5$ と $+3$

\begin{eqnarray} & & x^2 +8x+15 \\ &=& (x+5)(x+3) \end{eqnarray}

$$ \mbox{例5-2）} \ x^2 -5x+4 $$

足して $-5$ 、かけて $+4$ になる２数は？
→ $-4$ と $-1$

\begin{eqnarray} & & x^2 -5x+4 \\ &=& (x-4)(x-1) \end{eqnarray}

$$ \mbox{例5-3）} \ x^2 +4x-12 $$

足して $+4$ 、かけて $-12$ になる２数は？
→ $+6$ と $-2$

\begin{eqnarray} & & x^2 +4x-12 \\ &=& (x+6)(x-2) \end{eqnarray}

よくできた！

じゃ応用編として例題６もやってみようか。

いちおう、準備練習もしとく？

以下の２つの「足して・かけて」をそれぞれ答えてから、いこう。

\begin{eqnarray} & & +7y \mbox{と} +2y \quad -3y \mbox{と} -2y \quad -10y \mbox{と} -5y \\ & & +5y \mbox{と} -3y \quad -2y \mbox{と} +y \quad -9y \mbox{と} +4y \end{eqnarray}

例題６）次の式を因数分解しなさい。

$x^2 +9xy+14y^2$
$x^2 -11xy+24y^2$
$x^2 -xy-2y^2$

\begin{eqnarray} \mbox{例6-1）}& & x^2 +9xy+14y^2 \\ &=& (x+7y)(x+2y) \\ \mbox{例6-2）}& & x^2 -11xy+24y^2 \\ &=& (x-8y)(x-3y) \\ \mbox{例6-3）}& & x^2 -xy-2y^2 \\ &=& (x-2y)(x+y) \end{eqnarray}

よくできた！

あとは問題をたくさんやって「わかる」を「できる」にしていこう。

中3数学完全攻略定期テスト対策

posted with カエレバ

楽天市場

Amazon

注意点と練習問題

この例題５・例題６はいままででいちばん時間がかかるでしょう。

準備練習をしっかり積めばできるようになりますが、それでもなかなかコツがつかめないという生徒には、以下のアドバイスをしてあげてください。

$x^2 +8x+15$ などの場合…
・かけて $+15$ になる２数をまず考える
・そのうち足して $+8$ になるものが当たり
→ $+5$ と $+3$
$x^2 -5x+4$ などの場合…
・かけて $+4$ 足して $-5$ だから、２数はマイナスとマイナス
→ $-4$ と $-1$
$x^2 +4x-12$ などの場合…
・かけて $-12$ だから、２数はプラスとマイナス
・そのうえ足して $+4$ だから、数だけの引き算（＝絶対値の差）で4になる２数
・しかも絶対値はプラスのやつのほうが大きい
→ $+6$ と $-2$

こうしたアドバイスは、一緒に練習問題を解きながらしてあげるといいでしょう。

慣れてきたら、自力でさせてみてください。

（公式３とあるリンク先は、３つの公式のまとめ問題になっています）

○因数分解(公式1)

○因数分解(公式3)