中3数学「多項式」の5回目。
今回は因数分解の応用問題のやり方を解説します。
応用問題とは、こんなの↓
- 例2-1)\( 3x^2 -75 \)
- 例3-1)\( (x+1)^2 +4(x+1) +3 \)
- 例4-1)\( 2a(b-5) -3b+15 \)
つまり、
- 共通因数でくくってさらに公式を使う問題
- 置き換えを使う問題
- 部分的に因数分解する問題
の3つです。
ただ、いきなりこんな応用問題に入っても、たいていの生徒はつまずきます。
中学生はまず、因数分解の基本を習ったあと、どの方法を使うか見分けるやり方を学ぶべき。
そこでこの記事ではさいしょに因数分解の見分け方のコツを紹介します。
そのあと応用問題それぞれのやり方にすすみましょう。
≪「多項式」の記事一覧≫
- 中学数学「多項式」の教え方① 展開の基本
- 中学数学「多項式」の教え方② 乗法公式
- 中学数学「多項式」の教え方③ 展開の応用問題
- 中学数学「多項式」の教え方④ 因数分解
- 中学数学「多項式」の教え方⑤ 因数分解の応用問題
- 中学数学「多項式」の教え方⑥ 式の計算の利用
因数分解の見分け方

じっさいのテストでは、こんなふうにいきなり問題が出されるだけ。
因数分解のどの方法を使うかは自分で考えないといけません。
そこで、考えるときのフローチャートを作ってみました↓
因数分解はこの流れにそってやるだけです。
以下、例題1をやってみましょー。
共通因数は…ある。\(x\) 。
→ \( x^2 -16x = x(x-16) \)
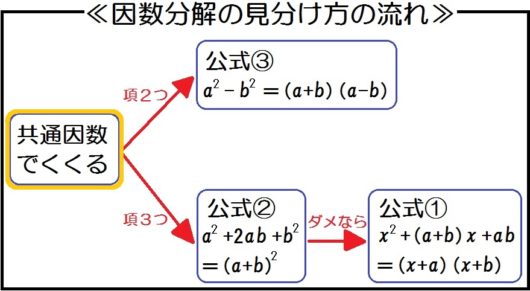
共通因数は…ない。
項は…2つ。
公式③が…使える。
→ \( x^2 -16 = (x+4)(x-4) \)
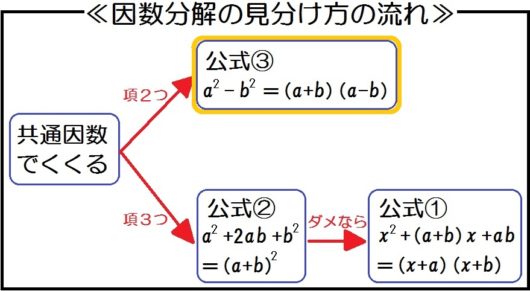
共通因数は…ない。
項は…3つ。
公式②が…使える。
→ \( x^2 -8x+16 = (x-4)^2 \)
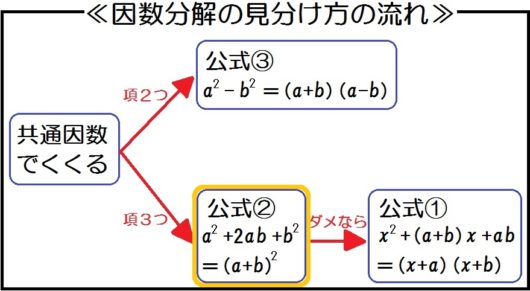
共通因数は…ない。
項は…3つ。
公式②が…使えない。
公式①は…使える。
→ \( x^2 -10x+16 = (x-8)(x-2) \)
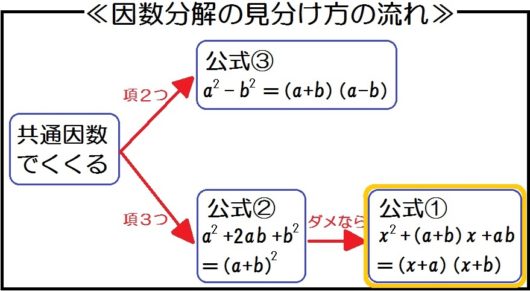
以上です。
かんたんでしょ。
指導者や保護者の方もぜひ参考にしてください。
では練習問題をたくさんやって、チャートを見なくてもパッとできるようになりましょう。
例によってまた「中学校数学学習サイト」というサイト様の練習問題ページを貼っておきます。問題のチョイスがいいんですよね、このサイト。このあとの応用問題も同様に貼っときます。
「共通因数→公式」の問題

因数分解の見分け方が身についたら、いよいよ応用問題です。
応用ひとつめは、共通因数でくくってさらに公式を使う問題。
ロンよりショウコ。
じっさいにやってみせましょう。
共通因数は…ある。\(3\) 。
→ \( 3x^2 -75 = 3(x^2 -25) \)
これで終わりじゃない。
カッコの中、まだ公式③が使える。
→ \(= 3(x+5)(x-5) \)
まだ因数分解できる?できないね。これで終わり。
\begin{eqnarray} & & 3x^2 -75 \\ &=& 3(x^2 -25) \\ &=& 3(x+5)(x-5) \end{eqnarray}
共通因数は…ある。\(5y\) 。
→ \( 5x^2 y +10xy +5y = 5y(x^2 +2x+1) \)
これで終わりじゃない。
カッコの中、まだ公式②が使える。
→ \(= 5y(x+1)^2 \)
まだ因数分解できる?できないね。これで終わり。
\begin{eqnarray} & & 5x^2 y +10xy +5y \\ &=& 5y(x^2 +2x+1) \\ &=& 5y(x+1)^2 \end{eqnarray}
共通因数は…ある。\(x\) 。
→ \( x^3 +10x^2 -11x = x(x^2 +10x-11) \)
これで終わりじゃない。
カッコの中、まだ公式①が使える。
→ \(= x(x+11)(x-1) \)
まだ因数分解できる?できないね。これで終わり。
\begin{eqnarray} & & x^3 +10x^2 -11x \\ &=& x(x^2 +10x-11) \\ &=& x(x+11)(x-1) \end{eqnarray}
共通因数は…ある。\(\frac{1}{8}xy\) 。
→ \( \frac{1}{8} x^3 y + \frac{1}{4} x^2 y -xy = \frac{1}{8}xy (x^2 +2x-8) \)
これで終わりじゃない。
カッコの中、まだ公式①が使える。
→ \(= \frac{1}{8}xy (x+4)(x-2) \)
まだ因数分解できる?できないね。これで終わり。
\begin{eqnarray} & & \frac{1}{8} x^3 y + \frac{1}{4} x^2 y -xy \\ &=& \frac{1}{8}xy (x^2 +2x-8) \\ &=& \frac{1}{8}xy (x+4)(x-2) \end{eqnarray}
以上のように、共通因数でくくったあともカッコの中で公式を使えるなら使うこと。
使わずにそのままにしたら、テストで✔になるので、気をつけて。
因数分解の問題では「もう因数分解できないかな」と、出た答えをつねに確認するようにしましょう。
なお例題2-4は \(\frac{1}{8}xy\) でくくりました。
これは、カッコの中を整数だけにしたいから。
一般的に、共通因数でくくる場合はカッコの中に分数を残さないようにする。これ、数学上のマナーのひとつなので覚えておきましょう。
では練習問題をどうぞ。
置き換えを使う問題

因数分解の応用ふたつめは、置き換えを使う問題です。
置き換えのやり方は展開の応用問題でもやりましたね。
共通部分をみつけたら大文字で置き換えるんだと。
以下、例題3をやってみましょう。
ポイント:共通部分を置き換えて、公式①
\begin{eqnarray} & & x+1=M\mbox{と置くと} \\ &=& M^2 +4M+3 \\ &=& (M+3)(M+1) \\ &=& \{ (x+1)+3 \} \{(x+1)+1 \} \\ &=& (x+1+3)(x+1+1) \\ &=& (x+4)(x+2) \end{eqnarray}
ポイント:共通部分を置き換えて、公式②
\begin{eqnarray} & & 2x-3=M\mbox{と置くと} \\ &=& M^2 -12M+36 \\ &=& (M-6)^2 \\ &=& \{ (2x-3)-6 \}^2 \\ &=& (2x-3-6)^2 \\ &=& (2x-9)^2 \end{eqnarray}
ポイント:カッコ2つをそれぞれ置き換えて、公式③
\begin{eqnarray} & & 2x+y=A , x-2y=B\mbox{と置くと} \\ &=& A^2 -B^2 \\ &=& (A+B)(A-B) \\ &=& \{ (2x+y)+(x-2y) \} \{(2x+y)-(x-2y) \} \\ &=& (2x+y+x-2y)(2x+y-x+2y) \\ &=& (3x-y)(x+3y) \end{eqnarray}
ポイント:共通部分を置き換えて、共通因数でくくる→公式③
\begin{eqnarray} & & a-b=M\mbox{と置くと} \\ &=& x^2 M -y^2 M \\ &=& M(x^2 -y^2) \\ &=& (a-b)(x^2 -y^2) \\ &=& (a-b)(x+y)(x-y) \end{eqnarray}
以上が置き換えを使う因数分解です。
例題3全体の注意点としては、
- 「 \(x+1=M\)と置くと」などのセリフをちゃんと書く
- 大文字を元に戻すときに小カッコを忘れない
- はじめに共通因数がないことも確認
という3つです。
また例題3-3は問題全体が (二乗)-(二乗) の形だったので、共通部分ではなくカッコそれぞれを大文字A,Bで置き換えました。
そして例題3-4は「置き換え」と「共通因数でくくってさらに公式を使う」の合わせわざでした。
この二問ができれば因数分解の応用はOKといえるでしょう。
あとは練習問題をやって「わかる」を「できる」にしていってください。
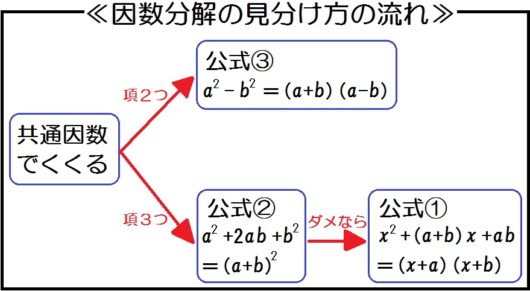
因数分解の見分け方の流れ
さて。
こっからはさらに発展した話。
偏差値55以上の高校をねらう人だけ聞いてください。
それ以外の人はまとめに飛んでかまいません。
何かというと、例題3-3と例題3-4、置き換えを使わなくてもできるようになってほしいってコト。
つまりこんなかんじで↓
\begin{eqnarray} \mbox{例3-3)} \ & & (2x+y)^2 -(x-2y)^2 \\ &=& \{ (2x+y)+(x-2y) \} \{(2x+y)-(x-2y) \} \\ &=& (2x+y+x-2y)(2x+y-x+2y) \\ &=& (3x-y)(x+3y) \end{eqnarray}
\begin{eqnarray} \mbox{例3-4)} \ & & x^2 (a-b) -y^2 (a-b) \\ &=& (a-b)(x^2 -y^2) \\ &=& (a-b)(x+y)(x-y) \end{eqnarray}
慣れてきたらこれもできるよ!
そんな人だけ、最後の例題4「部分的に因数分解」を読んでほしいと思います。
難問:部分的に因数分解

さいごの例題4は難問です。
置き換えを使わなくてもそのままできるという中学生。
そして平均以上の高校進学をめざす中学生だけやってみてください。
コツは「部分的に因数分解してムリヤリ共通部分をつくる」ことです。
ポイント:\(b-5\) が後半にもほしい→後半だけ \(-3\) でくくる!
\begin{eqnarray} & & 2a(b-5) -3b+15 \\ &=& 2a(b-5) -3(b-5) \\ &=& (b-5)(2a-3) \end{eqnarray}
ポイント:共通部分がない→とりあえず前半だけ \(x\) でくくる!
\begin{eqnarray} & & xy-x+y-1 \\ &=& x(y-1)+y-1 \\ &=& x(y-1)+(y-1) \\ &=& (y-1)(x+1) \end{eqnarray}
ポイント:\(x^2 -2xy+y^2 \) だけ因数分解できる!→共通部分が出たので公式①
\begin{eqnarray} & & x^2 -2xy+y^2 +x-y-12 \\ &=& (x-y)^2 +(x-y)-12 \\ &=& \{(x-y)+4\} \{(x-y)-3\} \\ &=& (x-y+4)(x-y-3) \end{eqnarray}
ポイント:項を入れかえたら \(x^2 -2x+1 \) がある!→(二乗)-(二乗)の形になったので公式③
\begin{eqnarray} & & x^2 -y^2 -2x+1 \\ &=& x^2 -2x+1 -y^2 \\ &=& (x-1)^2 -y^2 \\ &=& \{(x-1)+y\} \{(x-1)-y\}\\ &=& (x-1+y)(x-1-y) \end{eqnarray}
このように、部分的に因数分解すると共通部分(または(二乗)-(二乗)の形)が出てくることがあります。
共通因数がない。
公式も使えない。
置き換えようにも共通部分が見当たらない…。
そんな難問に出合ったら、この「部分的に因数分解」の方法を使ってください。
では、さいごの練習問題をどうぞ。
まとめ

因数分解の応用問題のコツは以下の4つ。
①どの因数分解の方法を使ったらいいか?
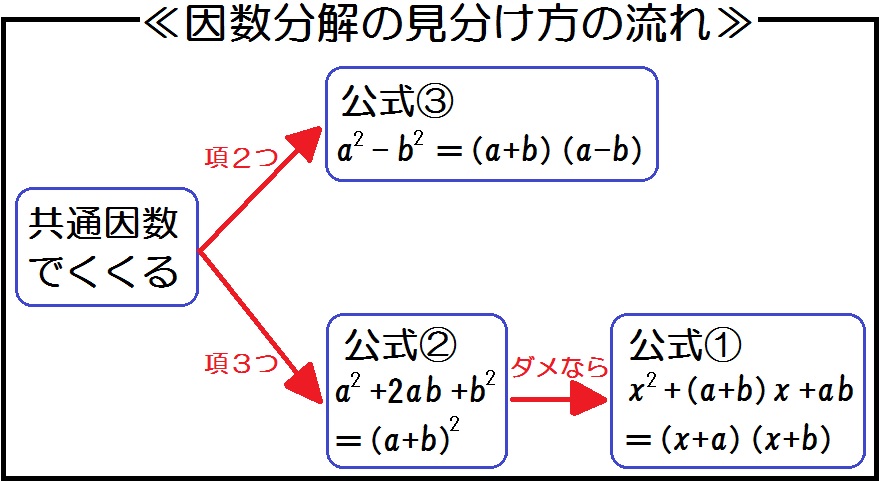
見分けるコツは、この流れに沿うだけ↓

因数分解の見分け方の流れ
②共通因数でくくったあとも公式を使えるなら使う。
\begin{eqnarray} & & 3x^2 -75 \\ &=& 3(x^2 -25) \\ &=& 3(x+5)(x-5) \end{eqnarray}
③共通部分(または(二乗)-(二乗) の形)を見つけたら、置き換えを使って因数分解。
\begin{eqnarray} & &(x+1)^2 +4(x+1) +3 \\ & & x+1=M\mbox{と置くと} \\ &=& M^2 +4M+3 \\ &=& (M+3)(M+1) \\ &=& \{ (x+1)+3 \} \{(x+1)+1 \} \\ &=& (x+1+3)(x+1+1) \\ &=& (x+4)(x+2) \end{eqnarray}
④部分的に因数分解して、ムリヤリ共通部分(または(二乗)-(二乗) の形)をつくる。
\begin{eqnarray} & & 2a(b-5) -3b+15 \\ &=& 2a(b-5) -3(b-5) \\ &=& (b-5)(2a-3) \end{eqnarray}
次回は中3多項式単元のさいご。
「式の計算の利用」を解説します。
いろんな種類の問題がある「式の計算の利用」ですが、高校入試と高校数学につながるものは何かという観点で、ポイントをしぼってコツを紹介していきます。
≪「多項式」の記事一覧≫
- 中学数学「多項式」の教え方① 展開の基本
- 中学数学「多項式」の教え方② 乗法公式
- 中学数学「多項式」の教え方③ 展開の応用問題
- 中学数学「多項式」の教え方④ 因数分解
- 中学数学「多項式」の教え方⑤ 因数分解の応用問題
- 中学数学「多項式」の教え方⑥ 式の計算の利用




コメント
いつも参考になります。
4x^2+12x+9や、16x^2-25、みたいなやつは扱わないですか?
なお、例2-3、符号をご確認ください。
ご指摘ありがとうございます。符号、修正します。