中3数学「多項式」の2回目。
今回は乗法公式を解説します。
- \( (x+a)(x+b) = x^2 +(a+b)x +ab \)
- \( (a+b)^2 = a^2 +2ab +b^2 \)
- \( (a+b)(a-b) = a^2 – b^2 \)
多項式の前半で学ぶ、こんな公式3つ。
ここでの目標は、この公式をおぼえることではありません。
この公式を使って一瞬で展開できるようになることです。

だから必要なのは、圧倒的な練習量。
ちょうどピアニストが指の動きを考えたりしないように、サッカー選手が「どうやって蹴ろうか」なんて考えこんだりしないように、問題を見たら条件反射で解けるようになるまで、練習するんです。
以下では、乗法公式それぞれが出てくるワケと、使い方のコツを解説します。
しかしこの記事で満足せず、内容を理解したらすぐに練習をはじめてください。
それが、次の段階でつまずかないための最善策です。
では、前置きはこれくらいにして、いきましょー。
乗法公式1の基本

まず乗法公式の1つめ、
$$ (x+a)(x+b) = x^2 +(a+b)x +ab $$
これが出てくる理由と、使い方を説明します。
講師・教師・保護者の方は以下の流れを指導にお役立てください。
指導例:公式1の導入
前回は展開の基本を学んだ。
今回はそれを使って、「展開がちょっとカンタンにできるようになる公式」を3つ学んでいきます。
まず公式1つめから。
例題1)次の式を展開しなさい。
- \( (x+5)(x+2) \)
- \( (x-3)(x-6) \)
- \( (x+5)(x-3) \)
この例題はどれも、カッコ内の前半が \(x\) でそろってるね。
ま、とりあえず展開してみよう。

よくできた。
でもせっかくなら、もっとカンタンに計算したい。
2行目の式なんか書かずに、いきなり答えを出したい。
いい方法はないものか…。
そこで、それぞれの答えから考えてみよう。
$$ (x+5)(x+2) = x^2 +7x+10 $$
- \(x^2 \) ← \( (x)^2 \)
- \(+7x\) ← \( (+5+2) \times x \)
- \(+10\) ← \( (+5) \times (+2) \)
$$ (x-3)(x-6) = x^2 -9x+18 $$
- \(x^2 \) ← \( (x)^2 \)
- \(-9x\) ← \( (-3-6) \times x \)
- \(+18\) ← \( (-3) \times (-6) \)
$$ (x+5)(x-3) = x^2 +2x-15 $$
- \(x^2 \) ← \( (x)^2 \)
- \(+2x\) ← \( (+5-3) \times x \)
- \(-15\) ← \( (+5) \times (-3) \)
気づいた?
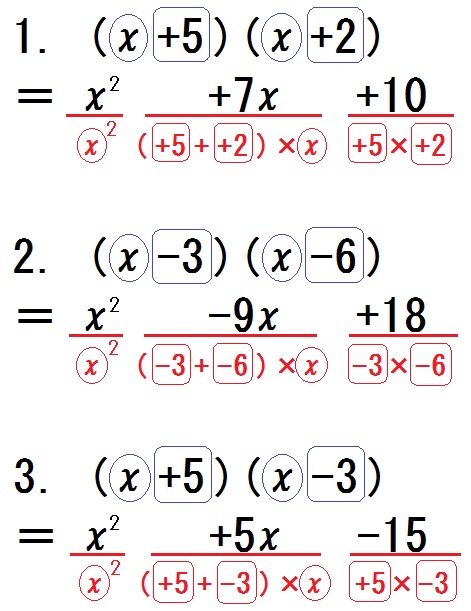
つまり
(\(\mbox{○}\)+■)(\(\mbox{○}\)+▲)= \(\mbox{○}^2\) +(■+▲)\(\mbox{○}\) +■▲
これが公式の1つめだ。
文字を使ってかっこよく書くと、
≪乗法公式1≫
\begin{eqnarray} & & (x+a)(x+b) \\ &=& x^2 +(a+b)x +ab \end{eqnarray}
となるわけ。
指導例:公式1の使い方
今度はこの公式を使って、もういちど例題1を解いてみよう。
$$ \mbox{例1-1)} \ (x+5)(x+2) $$
まず、前を二乗して: \(x^2\)
うしろを足して、\( \times x\) : \(+7x\)
うしろをかけて: \(+10\)
→ \(x^2 +7x+10 \)
$$ \mbox{例1-2)} \ (x-3)(x-6) $$
前を二乗して: \(x^2\)
うしろを足して、\( \times x\) : \(-9x\)
うしろをかけて: \(+18\)
→ \(x^2 -9x+18 \)
$$ \mbox{例1-3)} \ (x+5)(x-3) $$
前を二乗して: \(x^2\)
うしろを足して、\( \times x\) : \(+2x\)
うしろをかけて: \(-15\)
→ \(x^2 +2x-15 \)
よくできた!
なお、この公式はカッコ内の前半がそろっていたら使える。
だから式の形をよく見ること。
ちなみにカッコ内の前半は \(x\) じゃなくてもいいからね。
ってことで、類題も一緒に解いてみよう。
類題1)次の式を展開しなさい。
- \( (a+2)(a+7) \)
- \( (p-5)(p-8) \)
- \( (y-4)(y+3) \)
$$ \mbox{類題1-1)} \ (a+2)(a+7) $$
前を二乗して: \(a^2\)
うしろを足して、\( \times a\) : \(+9a\)
うしろをかけて: \(+14\)
→ \(a^2 +9a+14 \)
$$ \mbox{類題1-2)} \ (p-5)(p-8) $$
前を二乗して: \(p^2\)
うしろを足して、\( \times p\) : \(-13p\)
うしろをかけて: \(+40\)
→ \(p^2 -13p+40 \)
$$ \mbox{類題1-3)} \ (y-4)(y+3) $$
前を二乗して: \(y^2\)
うしろを足して、\( \times y\) : \(-y\)
うしろをかけて: \(-12\)
→ \(y^2 -y-12 \)
最後に2つ注意点。
たとえば類題1-1)は「うしろを足して、\( \times x \) :\(+9x\) 」なんてしちゃう場合が多い。
前にある文字は \(a\) だから、かけるのは \(a\) 。気を付けよう。
また、類題1-3)は「 \(y^2 -1y-12 \) 」 と答えがち。
係数1は省略できるからね。忘れないように。
練習問題
ここまでくれば、あとは冒頭で書いたとおり、ひたすら練習です。
なお練習問題を解くさいには、
≪乗法公式1≫
(\(\mbox{○}\)+■)(\(\mbox{○}\)+▲)= \(\mbox{○}^2\) +(■+▲)\(\mbox{○}\) +■▲
\( (x+a)(x+b) = x^2 +(a+b)x +ab \)
を参照しながら解いてもいいでしょう。
ただいつまでも公式をチラ見していては、自力で解けるようになりません。
そこで、「公式1の使い方」で書いた言葉を使う。
つまり問題をみて「あ、カッコ内の前がそろってる!」と気づいたら
- 前を二乗して
- うしろを足して、\( \times \mbox{前}\)
- うしろをかけて
と頭の中で唱えながら書くんです。
スムーズに自力で解けるようになっていきますよ。
では、練習問題を20問用意しました。
プリントアウトしたりしてお使いください。
乗法公式1の応用

次に、乗法公式1を使った応用問題です。
例題2のような問題は、とくに2番目の項をまちがえやすい。
そこで実際の問題に出くわすまえに解説してあげるといいでしょう。
指導例:公式1の応用問題
ではここで、乗法公式1を使うけどちょっと難しめの問題もやってみよう。
例題2)次の式を展開しなさい。
- \( (x+4y)(x+5y) \)
- \( (3x-2)(3x-4) \)
- \( (2x+7y)(2x-y) \)
$$ \mbox{例2-1)} \ (x+4y)(x+5y) $$
まず前を二乗して、\(x^2\) 。
次にうしろを足すとなんぼ?そう、 \(+9y\) 。
それに \( \times x\) するから?
うん、\(+9xy\) になるね!
最後にうしろをかけて、\(+20 y^2\) 。
→答. \(x^2 +9xy+20 y^2 \)
このように、うしろにも文字がある場合ちょっと答えがちがってくる。
とくに2番目・3番目の項は注意が必要だ。
\(y\) を忘れて \(x^2 +9x+20 \) ってしちゃうミスが多いよ。
$$ \mbox{例2-2)} \ (3x-2)(3x-4) $$
まず前を二乗して、\(9x^2\) 。
次にうしろを足すとなんぼ? \(-6\) 。
それに \( \times 3x\) するから?
うん、\(-18x\) になるね!
最後にうしろをかけて、\(+8\) 。
→答. \(9x^2 -18x+8 \)
このように、前が \(3x\) とかの場合も答えがちょっとちがってくる。
とくに1番目・2番目の項は注意が必要だ。
\(3\) を忘れて \(x^2 -6x+8 \) ってしちゃうミスが多いよ。
$$ \mbox{例2-3)} \ (2x+7y)(2x-y) $$
まず前を二乗して、\(4x^2\) 。
次にうしろを足すとなんぼ? \(+6y\) 。
それに \( \times 2x\) するから?
うん、\(+12xy\) になるね!
最後にうしろをかけて、\(-7 y^2\) 。
→答. \(4x^2 +12xy-7 y^2 \)
例題2-3は例題2-1と例題2-2の合わせ技。
これができたら乗法公式1はバッチリだ。
すこしずつ慣れていこう。
練習問題
以上が乗法公式1の応用問題です。
わたしが公式を文字だけでなく、○・■・▲を使って、
≪乗法公式1≫
(\(\mbox{○}\)+■)(\(\mbox{○}\)+▲)= \(\mbox{○}^2\) +(■+▲)\(\mbox{○}\) +■▲
と書いたわけが、これでわかりますね。
カッコ内の前半が \(x\) だけとは限らないからです。
だからここでも、公式をチラ見するのではなく、
- 前を二乗して
- うしろを足して、\( \times \mbox{前}\)
- うしろをかけて
と頭の中で唱えながら書くといいでしょう。
基本問題にくらべて時間はかかりますが、たくさん問題を解くことで慣れていってください。
ではまた、練習問題を20問用意しました。
質問はコメント欄からどうぞ。
つづいて、乗法公式2【\((a+b)^2 = a^2 +2ab +b^2\)】の基本と応用を解説します。
≪「多項式」の記事一覧≫



コメント