乗法公式1・乗法公式2につづき、乗法公式3
$$ (a+b)(a-b)=a^2 -b^2 $$
この公式が出てくるワケと、使い方のコツを解説します。
さいごも基本・応用とスモールステップでどうぞー。
乗法公式3の基本

乗法公式3は、与えられた式の形がとりわけ特殊です。
また答えはとてもスッキリした形になります。
なので、基本問題はサクッと進むでしょう。
指導例:公式3の導入
さて、「展開がちょっとカンタンにできるようになる公式」のさいご。
3つめは、たとえば、こんな問題↓
例題5)次の式を展開しなさい。
- \( (x+3)(x-3) \)
- \( (x-8)(x+8) \)
- \( (2x+7y)(2x-7y) \)
式の形を見ると、カッコ内の前はやはり同じ。
そしてうしろも符号が異なるだけで、数字(と文字)は同じ。
こんな式を、まぁとりあえず公式使わずに展開してみよう。
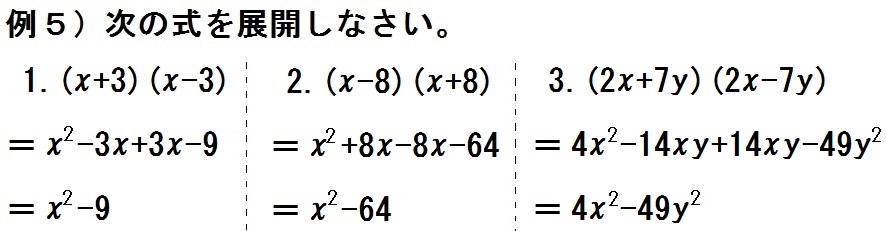
まんなかが消えて、スッキリした答えになったね。
この答えをまた、一発で出す方法を考えてみよう。
$$ (x+3)(x-3) = x^2 -9 $$
- \(x^2 \) ← \( x \times x \)
- \(-9\) ← \( +3 \times -3 \)
$$ (x-8)(x+8) = x^2 -64 $$
- \(x^2 \) ← \( x \times x \)
- \(-64\) ← \( -8 \times +8 \)
$$ (2x+7y)(2x-7y) = 4x^2 -49 y^2 $$
- \(4x^2 \) ← \( 2x \times 2x \)
- \(-49 y^2\) ← \( +7y \times -7y \)
気づいたね?
≪乗法公式3≫
(■+▲)(■-▲) = ■\(^2\) – ▲\(^2\)
\( (a+b)(a-b) = a^2 – b^2 \)
となるんだ。
指導例:公式3の使い方
今度はこの公式を使って、もういちど例題5を解いてみよう。
$$ \mbox{例5-1)} \ (x+3)(x-3) $$
同符号どうしをかけて: \(x^2\)
異符号どうしをかけて: \(-9\)
→ \(x^2 -9 \)
$$ \mbox{例5-2)} \ (x-8)(x+8) $$
同符号どうしをかけて: \(x^2\)
異符号どうしをかけて: \(-64\)
→ \(x^2 -64 \)
$$ \mbox{例5-3)} \ (2x+7y)(2x-7y) $$
同符号どうしをかけて: \(4x^2\)
異符号どうしをかけて: \(-49y^2\)
→ \(4x^2 -49y^2 \)
よくできた!
んじゃ類題も一緒に解いてみよう。
類題5)次の式を展開しなさい。
- \( (a-4)(a+4) \)
- \( (6p+9q)(6p-9q) \)
- \( (7+x)(7-x) \)
$$ \mbox{類5-1)} \ (a-4)(a+4) $$
同符号どうしをかけて: \(a^2\)
異符号どうしをかけて: \(-16\)
→ \(a^2 -16 \)
$$ \mbox{類5-2)} \ (6p+9q)(6p-9q) $$
同符号どうしをかけて: \(36p^2\)
異符号どうしをかけて: \(-81q^2\)
→ \(36p^2 -81q^2 \)
$$ \mbox{類5-3)} \ (7+x)(7-x) $$
同符号どうしをかけて: \(49\)
異符号どうしをかけて: \(-x^2\)
→ \(49 -x^2 \)
*最後の問題は
同符号どうし:\(7\) と \(7\)
異符号どうし:\(+x\) と \(-x\)
だから、こうなるよ。
練習問題
ひとつ余談を。
類題3-3のような問題は、教科書には出てきません。
またふつうの問題集にもあまりないと思います。
それでもあえて載せたのは、この連載の目的が「学力下位・中位の生徒を上位に引き上げるため」だから。
そのために必要なのは、深い理解とたくさんの練習、そして「こんな場合にも公式が使えるんだ」というような広い視野です。
このあとの乗法公式3の応用問題も、そうした広い視野を持ってほしいために載せました。
指導者・保護者の方はジュウゴのこのスタンスをご理解のうえ、当連載を活用していただけばと思います。
*数学の指導法連載一覧は数学まとめページから
乗法公式3の応用

というわけで、さいごに乗法公式3を使った応用問題です。
あまり見かけない問題ばかりですが、
- 同符号どうしをかけて
- 異符号どうしをかけて
という言葉を使えば、こうした応用問題も公式3で扱うことができます。
指導例:公式3の応用問題
では、公式3もちょっと難しめの問題。
例題6)次の式を展開しなさい。
- \( (-x+6)(x+6) \)
- \( (-2x-5y)(2x-5y) \)
- \( (-3x-7y)(7y-3x) \)
$$ \mbox{例6-1)} \ (-x+6)(x+6) $$
異符号どうしをかけて: \(-x \times x = -x^2\)
同符号どうしをかけて: \(+6 \times +6 = +36\)
→ \(-x^2 +36 \)
このように、異符号が前にくることもある。
そんな場合でも
「異符号どうしかけたら \(- \mbox{▲}^2\) 」
「同符号どうしかけたら \(+ \mbox{■}^2\) 」
というように公式3が使えるんだ。
$$ \mbox{例6-2)} \ (-2x-5y)(2x-5y) $$
異符号どうしをかけて: \(-2x \times 2x = -4x^2\)
同符号どうしをかけて: \(-5y \times -5y = +25y^2\)
→ \(-4x^2 +25y^2 \)
このように、同符号がマイナスどうしになることもある。
そんな場合にも公式3が使えるよ。
$$ \mbox{例6-3)} \ (-3x-7y)(7y-3x) $$
この問題は一見すると公式3が使えそうにない。
でも、うしろのカッコ内の順番を入れかえて
$$ = (-3x-7y)(-3x+7y) $$
にしたら?
同符号どうしをかけて: \(-3x \times -3x = +9x^2\)
異符号どうしをかけて: \(-7y \times +7y = -49y^2\)
→ \(9x^2 -49y^2 \)
このように、カッコ内の順番を入れかえてもいいんだ。
≪乗法公式3≫
(■+▲)(■-▲) = ■\(^2\) – ▲\(^2\)
\( (a+b)(a-b) = a^2 – b^2 \)
ってことで、以上から公式3を使える場面がわかったね。
カッコ内の順番を入れかえてもいいから、文字や数字がぜんぶ同じで、なおかつ同符号どうしと異符号どうしが1ペアずつあればいいんだ。
では、たくさん練習して「わかる」を「できる」にしていこう。
練習問題
なお、例題6-3は以下の方法でもOKです。
\begin{eqnarray} & & (-3x-7y)(7y-3x) \\ &=& (-7y-3x)(7y-3x) \\ &=& -49y^2 +9x^2 \end{eqnarray}
だから実は類題5-3も、文字を前にもってきたかったら以下のとおり。
\begin{eqnarray} & & (7+x)(7-x) \\ &=& (x+7)(-x+7) \\ &=& -x^2 +49 \end{eqnarray}
どちらでも正解です。
項をかたまりで捉える意識があれば理解できますね。
では、さいごの練習問題をどうぞ。
≪「多項式」の記事一覧≫
まとめ

おつかれさまでした。
ずいぶん長い記事になっちゃいましたが、ここまで練習問題をふくめてキチンと学習したあなたは、すでにかなり高いレベルにまで達しています。
まとめましょう。
≪乗法公式1≫
(\(\mbox{○}\)+■)(\(\mbox{○}\)+▲)= \(\mbox{○}^2\) +(■+▲)\(\mbox{○}\) +■▲
\( (x+a)(x+b) = x^2 +(a+b)x +ab \)
使う場面:カッコ内の前だけそろっているとき。
使い方:「前を二乗して」「うしろを足して、\( \times \mbox{前}\)」「うしろをかけて」
- \( (x+5)(x+2) = x^2 +7x+10\)
- \( (x-3)(x-6) = x^2 -9x+18\)
- \( (x+5)(x-3) = x^2 +2x-15\)
- \( (x+4y)(x+5y) = x^2 +9xy+20y^2\)
- \( (3x-2)(3x-4) = 9x^2 -18x+8\)
- \( (2x+7y)(2x-y) = 4x^2 +12xy-7y^2\)
≪乗法公式2≫
(■+▲)\(^2\) = ■\(^2\) +2■▲ +▲\(^2\)
\( (a+b)^2 = a^2 +2ab +b^2 \)
使う場面:カッコに二乗があるとき。
使い方:「前を二乗して」「前・うしろかけて、2倍」「うしろを二乗して」
- \( (x+5)^2 = x^2 +10x+25\)
- \( (x-4)^2 = x^2 -8x+16\)
- \( (x-1)^2 = x^2 -2x+1\)
- \( (x+7y)^2 = x^2 +14xy+49y^2\)
- \( (3x-2)^2 = 9x^2 -12x+4\)
- \( (2x+5y)^2 = 4x^2 +20xy+25y^2\)
≪乗法公式3≫
(■+▲)(■-▲) = ■\(^2\) – ▲\(^2\)
\( (a+b)(a-b) = a^2 – b^2 \)
使う場面:文字や数字がぜんぶ同じで、同符号どうしと異符号どうしが1ペアずつあるとき。
使い方:「同符号どうしをかけて」「異符号どうしをかけて」
- \( (x+3)(x-3) = x^2 -9\)
- \( (x-8)(x+8) = x^2 -64\)
- \( (2x+7y)(2x-7y) = 4x^2 -49y^2\)
- \( (-x+6)(x+6) = -x^2 +36\)
- \( (-2x-5y)(2x-5y) = -4x^2 +25y^2\)
- \( (-3x-7y)(7y-3x) = 9x^2 -49y^2\)
次回はこの乗法公式3つを使った複雑な展開を解説します。
が、そのまえに、もうひとつだけ言わせてください。
これらの公式を使って一瞬で問題が解ける。
そんな状態になってないと、次回以降に進んでもつまずく、と。
だからこの記事では練習問題を計120問ほど用意しました。
しかしこれでも足りません。
乗法公式をマスターするためには、あわせて何問くらい練習すればいいのか?
ジュウゴの個人的な感覚では、
- 学力上位者:約50~100問
- 学力中位者:約100~300問
- 学力下位者:約300~500問
くらいです。
よって、指導者・保護者の方はこの乗法公式で、中学生にしっかり時間をとらせてください。
ジュウゴも毎回ここでは2~5時間ほど使ってます。んで生徒が絶句するくらいの宿題を出してます。
でもそれを乗り越えたら、因数分解がおどろくほどスムーズ。
ぜひジュウゴの経験を参考いただけたらと思います。
≪「多項式」の記事一覧≫




コメント