前ページの、乗法公式1
$$ (x+a)(x+b) = x^2 +(a+b)x +ab $$
につづいて、乗法公式2
$$ (a+b)^2 = a^2 +2ab +b^2 $$
この公式が出てくるワケと、使い方のコツを解説します。
乗法公式2にも基本問題と応用問題があるので、スモールステップでいきますね。
乗法公式2の基本

まずは乗法公式2を使った基本問題から。
講師・教師・保護者の方は以下の流れも前ページ同様にご参考ください。
指導例:公式2の導入
つづいて、「展開がちょっとカンタンにできるようになる公式」の2つめ。
例題3)次の式を展開しなさい。
- \( (x+5)^2 \)
- \( (x-4)^2 \)
- \( (x-1)^2 \)
カッコの外に二乗があるけど、ようするにこーゆーこと↓
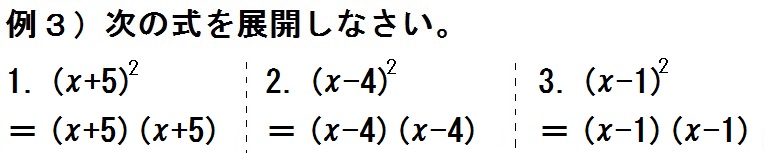
なので、とりあえず公式を使わずに展開してみよう。

さて、この展開もよりカンタンに一発でやりたい。
だからまた、それぞれの答えから考えてみよう。
$$ (x+5)^2 = x^2 +10x+25 $$
- \(x^2 \) ← \( (x)^2 \)
- \(+10x\) ← \( x \times (+5) \times 2 \)
- \(+25\) ← \( (+5)^2 \)
$$ (x-4)^2 = x^2 -8x+16 $$
- \(x^2 \) ← \( (x)^2 \)
- \(-8x\) ← \( x \times (-4) \times 2 \)
- \(+16\) ← \( (-4)^2 \)
$$ (x-1)^2 = x^2 -2x+1 $$
- \(x^2 \) ← \( (x)^2 \)
- \(-2x\) ← \( x \times (-1) \times 2 \)
- \(+1\) ← \( (-1)^2 \)
気づいた?
つまり
(■+▲)\(^2\) = ■\(^2\) +2■▲ +▲\(^2\)
文字を使って書けば、
≪乗法公式2≫
\begin{eqnarray} & & (a+b)^2 \\ &=& a^2 +2ab +b^2 \end{eqnarray}
となるわけ。
指導例:公式2の使い方
今度はこの公式を使って、もういちど例題3を解いてみよう。
$$ \mbox{例3-1)} \ (x+5)^2 $$
前を二乗して: \(x^2\)
前・うしろかけて、2倍: \(+10x\)
うしろを二乗して: \(+25\)
→ \(x^2 +10x+25 \)
$$ \mbox{例3-2)} \ (x-4)^2 $$
前を二乗して: \(x^2\)
前・うしろかけて、2倍: \(-8x\)
うしろを二乗して: \(+16\)
→ \(x^2 -8x+16 \)
$$ \mbox{例3-3)} \ (x-1)^2 $$
前を二乗して: \(x^2\)
前・うしろかけて、2倍: \(-2x\)
うしろを二乗して: \(+1\)
→ \(x^2 -2x+1 \)
よくできた!
ちなみにここで3つほど注意点。
- 2番目の項は「前・うしろをかけて、さらに2倍」だからね。2倍を忘れて「\(+5x\) (例1-1の場合)」としちゃうミスが多い。気をつけて。
- うしろが \(+5\) でも \(-4\) でも、二乗したらぜったいプラスになる。だから3番目の項はかならずプラスだ。
- 例3-3の場合、3番目の項は \( (-1)^2 =+1 \) だ。1の二乗は1。二乗と二倍をまちがえて \(x^2 -2x+2 \) としちゃう人が多い。これも気をつけよう。
ってことで、さいごに類題も一緒に解いてみよう。
類題3)次の式を展開しなさい。
- \( (a+3)^2 \)
- \( (b-7)^2 \)
- \( (-x-6)^2 \)
$$ \mbox{類3-1)} \ (a+3)^2 $$
前を二乗して: \(a^2\)
前・うしろかけて、2倍: \(+6a\)
うしろを二乗して: \(+9\)
→ \(a^2 +6a+9 \)
$$ \mbox{類3-2)} \ (b-7)^2 $$
前を二乗して: \(b^2\)
前・うしろかけて、2倍: \(-14b\)
うしろを二乗して: \(+49\)
→ \(b^2 -14b+49 \)
$$ \mbox{類3-3)} \ (-x-6)^2 $$
前を二乗して: \(x^2\)
前・うしろかけて、2倍: \(+12x\)
うしろを二乗して: \(+36\)
→ \(x^2 +12x+36 \)
練習問題
ここまでが乗法公式2の基本です。
教える側としては、上に書いたほかにあと2つ、ジュウゴが注意していることがあります。
1つ。
計算の苦手な子にとっては、2番目の項を一発で出すのがむずかしい。
そこで2段階に分けて発問するといいでしょう。
たとえば類題3-2なら
「前・うしろかけて?」→ \(-7b\)
「それを2倍すると?」→ \(-14b\)
というように。
生徒が慣れるまで10問でも20問でも、この発問を続けていけば、やがて自力でできるようになっていきます。
2つ。
\((a-b)^2 = a^2 -2ab +b^2\) というもうひとつの公式。
これをわたしは教えません。
なぜなら、項をかたまりで捉えないと、類題3-3が解けないから。
つまり「まんなかの符号が+か-か」というような意識でいる生徒は、類題3-3を
\begin{eqnarray} & & (-x-6)^2 \\ &=& x^2 -6x +9 \ \mbox{←まちがい} \end{eqnarray}
とミスしちゃうからです。
前回の記事でも言いましたが、項をかたまりで捉える意識、つねに大切にしてください。
≪乗法公式2≫
(■+▲)\(^2\) = ■\(^2\) +2■▲ +▲\(^2\)
\( (a+b)^2 = a^2 +2ab +b^2 \)
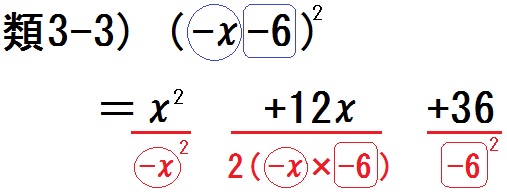
では、練習問題をどうぞ。
解く際には頭の中で
- 前を二乗して
- 前・うしろかけて、2倍
- うしろを二乗して
という言葉を利用してください。
乗法公式2の応用

(■+▲)\(^2\) の展開にも、前ページ同様、応用編があります。
これら応用問題も例題4としてまとめてみました。
実際の問題に出くわすまえの指導例として、ご参考ください。
指導例:公式2の応用問題
では公式1同様、公式2もちょっと難しめの問題をやってみよう。
例題4)次の式を展開しなさい。
- \( (x+7y)^2 \)
- \( (3x-2)^2 \)
- \( (2x+5y)^2 \)
$$ \mbox{例4-1)} \ (x+7y)^2 $$
前を二乗して: \(x^2\)
前・うしろかけて、2倍: \(+14xy\)
うしろを二乗して: \(+49 y^2\)
→ \(x^2 +14xy+49 y^2 \)
これ、\(y\) を忘れて \(x^2 +14x+49 \) としちゃいがち。
気をつけてね。
$$ \mbox{例4-2)} \ (3x-2)^2 $$
前を二乗して: \(9x^2\)
前・うしろかけて、2倍: \(-12x\)
うしろを二乗して: \(+4\)
→ \(9x^2 -12x+4 \)
これ、2番目の項を \(-6x\) とミスしがち。
前・うしろかけてから、さらに2倍するのを忘れないで。
$$ \mbox{例4-3)} \ (2x+5y)^2 $$
前を二乗して: \(4x^2\)
前・うしろかけて、2倍: \(+20xy\)
うしろを二乗して: \(+25 y^2\)
→ \(4x^2 +20xy+25 y^2 \)
例題4-3ができたら、乗法公式2の応用問題もバッチリだ。
あとはたくさん練習して、「できる」をさらに「スラスラできる」にしていこう。
練習問題
例題4-2,4-3などは基本問題よりもさらに、2番目の項を一発で出すのがむずかしくなります。
そんなときはやはり、
「前・うしろかけて?」→ \(-6x\)
「それを2倍すると?」→ \(-12x\)
というように分けて考えるといいでしょう。
では、乗法公式2の応用問題の練習です。
質問はコメント欄からどうぞ。
最後に、乗法公式3【\((a+b)(a-b)=a^2 -b^2\)】の基本と応用を解説します。
≪「多項式」の記事一覧≫



コメント