商品の問題につづいて、食塩水の問題と増減の問題をやっつけていきましょう。
食塩水の問題
1次方程式における「食塩水の問題」の解き方がわからない…。
%からどう式をつくればいいか見当もつかない…。
こんな中学生向けに、どこよりもわかりやすく食塩水の問題の解き方を解説します。
濃度とは?
濃度とは「溶液中の溶質の割合」。
つまり、溶液の量にたいして溶質の量は何倍かってこと。
ようするに、食塩水にたいして食塩は何倍かってことです。
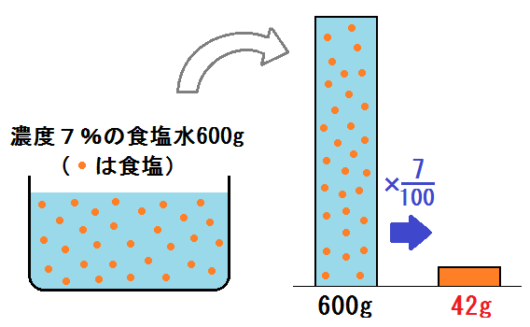
たとえば濃度7%の食塩水だったら、食塩の質量は \( \frac{7}{100}\) 倍です。
なので、濃度7%の食塩水600gの中には、食塩は
$$ 600 \times \frac{7}{100} = 42 \mbox{(g) 入ってます。}$$
また、濃度8%の食塩水 \(x\) g の中には、食塩は
$$ \frac{8}{100}x \mbox{(g)入っているし、}{}$$
濃度10%の食塩水 \(150+x\) g の中には、食塩は
$$ \frac{10}{100} (150+x) \mbox{(g)入ってます。}$$
じゃ、水200g の中に食塩はどんだけ入ってる?
そう、入ってない。だって水だし。
いちおう数学的にいうと濃度0%で \( \frac{0}{100}\) 倍ってこと。
じゃ、食塩28g の中に食塩はどんだけ入ってる?
そう、28g。あたりまえだね。
いちおう数学的にいうと濃度100%で \( \frac{100}{100}\) 倍ってこと。
ここまでわかれば、食塩水の問題を解く準備は完了です。
解き方のコツ
例題3)濃度が、6%の食塩水と10%の食塩水があります。この2種類の食塩水を混ぜあわせて、7%の食塩水を600gつくります。6%の食塩水と10%の食塩水の質量をそれぞれ求めなさい。(2018 埼玉 改)
それでは先に、食塩水問題の解き方のコツから伝えます。
下のような計6マスの表を書いて、ぜんぶうめること。
そして2行目(食塩)の行で方程式をつくること。
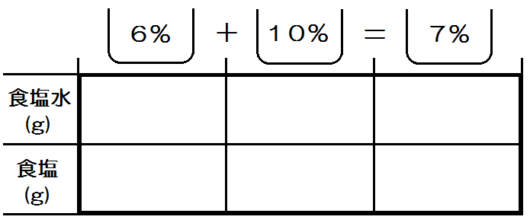
順をおってひとつずつ説明します。
まず表のつくり方ですが、左の項目には上に「食塩水」、下に「食塩」と書きます。これはどんな食塩水問題であってもおなじです。
また上の3項目には、文章にそって、食塩水の濃度を書き入れていきます。例題3では6%の食塩水と10%の食塩水を混ぜあわせて7%の食塩水をつくるので、「6%+10%=7%」のように書きます。
あとはわかるところから、この表の6マスぜんぶうめていくんです。
とりあえず、問題文にあるのは「7%の食塩水600g」ですね。
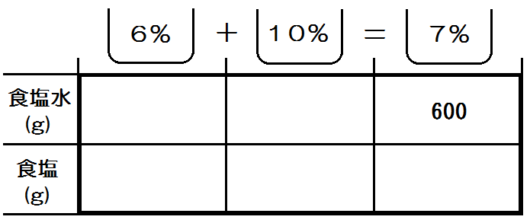
ここからは \(x\) の文字式も使って、残りのマスをうめていくことになります。
実はまだ求めるものを \(x\) で置いていませんでした。
例題3で求めるものは「6%の食塩水」と「10%の食塩水」の2つあります。
このような未知数2つの問題は過去記事(【個数】や【整数】や【平均】など)でさんざんやってきましたね。
そしてこの2つ、あわせたら600gになるんだから、もうわかりますね。
一方を \(x\) として、もう一方を \(600 -x\) とするんだと。
どっちでもいいですが、ここでは「6%の食塩水を \(x\) gとする」とします。
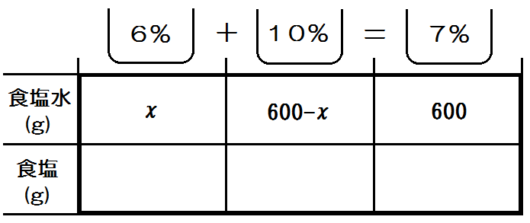
あとは下(食塩)の行の3つのみです。
たとえば濃度7%の食塩水600gの中にある食塩は?さっき復習しましたね。
3つぜんぶ表すとこのようになります。

こうして6マスぜんぶうまったら、下の食塩の行で等しい関係ができあがります。
なぜなら(6%の中にある塩)+(10%の中にある塩)=(7%の中にある塩)だから。
よって方程式とその後の解答は以下のとおり。
\begin{eqnarray} \frac{6}{100}x + \frac{10}{100}(600-x) &=& 600 \times \frac{7}{100} \\ 6x +10(600-x) &=& 600 \times 7 \\ 6x +6000 -10x &=& 4200 \\ 6x -10x &=& 4200 -6000 \\ -4x &=& -4800 \\ x &=& 450 \end{eqnarray}
また \(600 -450 = 150\)
答.6%の食塩水450g、10%の食塩水150g
以上のように、方程式文章題における食塩水の問題では、
計6マスの表を書いて、ぜんぶうめる。
2行目(食塩)の行で方程式をつくる。
この解き方のコツを利用して解決していってください。
練習問題
では、次の問題はどうでしょう。
類題2)3%の食塩水500gから何g の水を蒸発させると、5%の食塩水になるか。
今回は求めるものがひとつだけなんで、最初に「\(x\) g の水を蒸発させるとする」等と書きます。
次に、6マスの表をつくってうめていきます。
この類題が例題と大きくちがう点は2つ。
- 2つめが食塩水じゃなくて、水
- 混ぜあわせるんじゃなくて、蒸発させる
この2点に注意して表を完成させてみてください。
ジュウゴなら、こんなかんじの表を書きます。
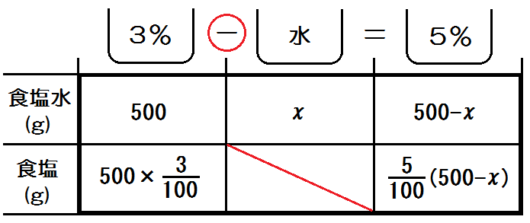
赤で示したとおり、「水だから中に食塩はない」「蒸発させるから+じゃなくて-」の2点が表現できていればOKです。
あとは、2行目(食塩)の行で方程式をつくるだけ。
\begin{eqnarray} 500 \times \frac{3}{100} &=& \frac{5}{100}(500-x) \\ 500 \times 3 &=& 5(500-x) \\ 1500 &=& 2500 -5x \\ 5x &=& 2500 -1500 \\ 5x &=& 1000 \\ x &=& 200 \end{eqnarray}
答.200g
以上のように、文章の内容に注意さえすれば、たとえ応用の効いた難問でも片づけられます。
6マスの表をうめて、食塩の行で方程式をつくる。
この解き方のコツでぜんぶやっつけていってください。
それでは練習問題をどうぞ。
問3)濃度15%の食塩水150gと、濃度8%の食塩水を混ぜあわせて、10%の食塩水をつくりたい。8%の食塩水を何g 混ぜればいいか。
問4)3%の食塩水360gに何g の食塩を加えると、10%の食塩水になるか。
問3)375g
問4)28g
*連立方程式の割合問題はこちら
増減の問題

最後に、方程式文章題の割合のなかでも「増減の問題」といわれるものを解説します。
増減問題は、商品・食塩水問題とちがって、わかりにくい言葉や概念はありません。
その代わり、何を \(x\) とすればいいかで迷います。
先に結論をいえば、増減問題では昔のほうを \(x\) とするというのが解き方のコツになります。
なぜ昔のほうを \(x\) とするべきなのか?
かんたんに説明してから、実際の解法に入っていきます。
昔と今、基準はどっち?
たとえば「スーパーカップ 1.5倍」という表記があります。
とうぜんラーメンの量が増えたってことですが、これ、いったい何とくらべて1.5倍になったのか?
昔の量とくらべて1.5倍になったんですね。
昔発売したふつうの量が72gで、その1.5倍になったんで、いまは
$$ 72 \times 1.5 = 108 \mbox{(g)というわけです。}$$
あるいは「身長が1年間で5%伸びた」とします。
これも何とくらべて5%増えたのか?
昨年の身長とくらべて、ですね。
なので昨年の身長を160cmとするなら、その5%増しなので、
$$ 160 \times \frac{105}{100} = 168 \mbox{(cm)が今年の身長となります。}$$
ついでに何cm伸びたかというと
$$ 160 \times \frac{5}{100} = 8 \mbox{(cm)伸びたと計算できます。}$$
このように、時間経過にともなって何かの量が増減するとき、基準はつねに昔のほうなんです。「昔の1.5倍」「昔の5%増し」なんです。
これが、増減の問題では昔のほうを \(x\) とするべき理由です。
解き方のコツ
例題4)ある学校の昨年の生徒数は男女合わせて140人であった。今年の生徒数は昨年と比べて、男子が5%増え、女子が10%減ったので、今年の生徒数は男女合わせて135人であった。今年の男子の生徒数は何人か、求めなさい。(2018 大分)
よってこの例題ではまず、「昨年の男子の生徒数を \(x\) 人」とします。
また昨年の女子の生徒数も未知数なので、「昨年の女子の生徒数は \(140-x\) と表せる」。(あわせて140人だから)
あとは方程式を立てるだけです。
昨年とくらべて、男子は5%増、女子は10%減で、合計135人だから、
$$ \frac{105}{100}x + \frac{90}{100}(140-x) = 135 $$
この方程式を解き、最後に今年の男子の生徒数を出して答えとなります。
\begin{eqnarray} \frac{21}{20}x + \frac{9}{10}(140-x) &=& 135 \\ 21x +18(140-x) &=& 2700 \\ 21x +2520 -18x &=& 2700 \\ 21x -18x &=& 2700 -2520 \\ 3x &=& 180 \\ x &=& 60 \end{eqnarray}
よって今年の男子生徒数は \( \frac{105}{100} \times 60 = 63 \)
答.63人
求めるものは「今年の」男子生徒数なので、最後の計算を忘れないようにしましょう。
また、増減の問題では別の解き方もあります。
増減だけに注目して式をつくる方法です。
男子の増えた人数は \( \frac{5}{100}x \) 。
女子の減った人数は \( \frac{10}{100}(140-x) \) 。
あわせて、差し引き \(140-135=5\) 人、減っています。
よって、増減だけに注目して方程式をつくると
$$ \frac{5}{100}x – \frac{10}{100}(140-x) = -5 $$
女子は減っているから-、合計も減っているから-をつけることを忘れずに。あとは同様です。
\begin{eqnarray} \frac{1}{20}x – \frac{1}{10}(140-x) &=& -5 \\ x -2(140-x) &=& -100 \\ x -280 +2x &=& -100 \\ x +2x &=& -100 +280 \\ 3x &=& 180 \\ x &=& 60 \end{eqnarray}
よって今年の男子生徒数は \(60 + \frac{5}{100} \times 60 = 63\)
答.63人
こっちの式のほうが計算がちょっとラクですね。
以上のように、方程式の割合における増減問題では、
たとえ求めるものが今年の数であっても、昔のほうを \(x\) とすること。
合計に注目した方程式、増減だけに注目した方程式と2通りの解法がある、後者がちょっとラク。
この2点が解き方のコツです。
練習問題
それでは、最後の練習問題です。
解答は末尾に記載、質問はコメント欄からどうぞ。
問5)ある工場でA、B2つの製品を作っている。先週は3000個作ったが、今週はAを15%増やし、Bを5%減らして合計3170個作った。今週のA、Bの個数をそれぞれ求めよ。
問6)ある学校では、春と秋の資源回収で、新聞紙と雑誌を回収しました。春に回収した新聞紙と雑誌の重さは合わせて17500kgでした。春と比べて、秋に回収した新聞紙の重さは1.5倍になり、雑誌の重さは2倍になったため、合わせて11000kg増えました。秋に回収した新聞紙の重さは何kgですか。(2017 山形)
問5)A:1840個、B:1330個
問6)19500kg
*連立方程式の割合問題はこちら
まとめ

おつかれさまでした。
中学数学の1次方程式の文章題、割合における解き方のコツをまとめます。
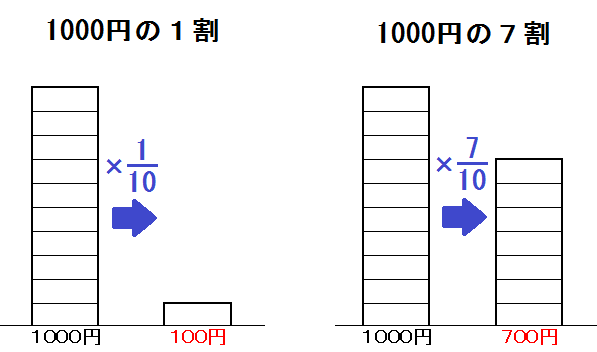
<割合>とは、ようするに何倍かってこと。
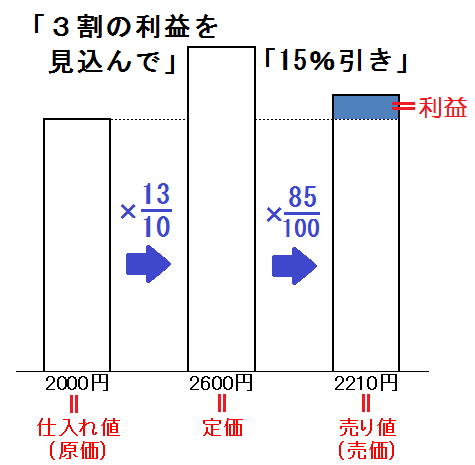
<商品の売買の問題>では、まず「原価」「定価」「売り値」「利益」「損失」5つの意味を知ること。
また原価や利益がからむ問題では、(売り値)-(原価)=(利益)という関係式を使って方程式をつくること。
<食塩水の問題>では、計6マスの表を書いてぜんぶうめること。
そして2行目の食塩の行で方程式をつくること。
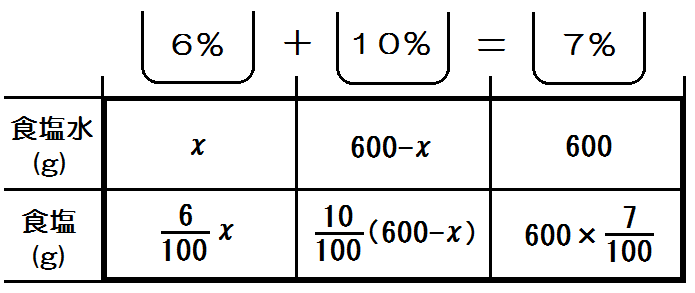
<増減の問題>では、求めるものが今年の数でも、昔のほうを \(x\) とすること。
また解き方は2通りあり、増減だけに注目した方程式のほうがちょっと計算がラク。
以上のコツだけまとめてもよかったんですが、中学生にはその理由まで知っておいてほしかったんで長い記事になってしまいました。
特に考える力のある子、数学の基礎はできている子にはぜひ「なぜそうなのか」まで知ることを欲してほしい。それが数学にかぎらず、知的能力の発達につながっていきます。
毎年、受験がせまってくるたびに切実にそう感じます…。
さて、次回はいよいよ方程式文章題の最後、【図形の問題】を解説します。
1次方程式文章題における図形問題には、長さや面積から等式を立てたり、周上を点が移動する問題などがあります。
それぞれのコツをイラスト付きでわかりやすく解説します。
[関連記事]
- 文章題①【代金、個数】
- 文章題②【分配、年齢、貯金】
- 文章題③【整数、自然数】
- 文章題④【平均の問題】
- 文章題⑤【過不足の問題】
- 文章題⑥【速さ・時間・道のり】
- 文章題⑦【速さ・時間・道のり】2
- 文章題⑧【割合の問題】
- 文章題⑨【図形の問題】
- *連立方程式の割合問題はこちら








コメント
問1)あるシャツを、以下のように販売する店がある。【通常2枚買う場合:定価の合計金額から500円引き】/【特別期間に3枚買う場合:定価の合計金額から40%引き】。このシャツを特別期間に3枚買う場合は、通常2枚買う場合よりも300円安くなるという。シャツ1枚の定価はいくらか。(2017 鹿児島)
この問題は通常と特別期間のシャツ一枚の価格を=関係にして解けばいいのですか? (2x−500)/2 =(3xー60/100) /3 +300 という式になったのですが答えが一致しません 教えてください
食塩の問題4の計算式を教えてください。360✖️3/100+X=(360+X)✖️10/100でたてたのですが、答えが合いません。
返信が遅くなり申し訳ありません。
そらとさんの式で、合っています。
方程式の計算のどこかでミスをされているかもです。
こんにちは!いつも読ませてもらってます!わかりやすくて参考になります。
練習問題問1)の式がたてられないです・・・なぜか全部、マイナスになってしまいます。式を教えていただけますか?
なっちさま
解答例)シャツ1枚の定価をx円とする。
3x × 100分の60 = (2x-500)-300
この式は
(特別期間に3枚買う場合)=(通常2枚買う場合)-300
で立式しました。
2Xー500=3×60/100×X+300
の間違いでした
3枚買うほうが300円安いんだから、2枚=○+300としなければ、ですね。有難うございました‼️
割合 問1 シャツの割合の問題の途中式教えてください。
定価をX円とすると、
2xー500=3×60/100 ×Xー300
X=1000 となるのですが。
質問失礼します。
練習問題②の途中式を教えてもらえますか?
何度やっても解けなかったのでよろしくお願いいたします。
>す様
問2)ある商品に、仕入れ値の25%の利益を見込んで定価をつけたが、安売りのとき、定価より360円安く売ったので、仕入れ値の5%の損失になった。この商品の仕入れ値は何円か、求めよ。
解答例)この商品の仕入れ値をx円とする。
(100分の125x -360)-x = -100分の5x
このあとどう解いてもいいですが、たとえば両辺100倍すると、
125x-36000-100x = -5x
125x-100x+5x = 36000
30x = 36000
x=1200
となります。
すみません
中学一年生なんですけど
原価を求める方法が分らないので教えていただければ嬉しいです
>原価を求める方法が分らないので教えていただければ嬉しいです
海斗さん
わからないところを具体的に言ってもらえれば、解説します。
中学2年生です。今は中1の一次方程式を完璧にしようと復習しているので、分からないところがあったときはよくこのブログに助けられています。
質問があります。
ある学校では、昨年度の男子の生徒数は、女子より200人多く、今年度は、昨年度より男子が3%、女子が4%減り、合計で48人減ったという。この学校の今年度の生徒数を求めよ。
という問題を解いたのですが、このサイトに載っていることを参考にして、3%減→100分の97、
4%減→100分の96として解いたところ、私は式を立てて解いたところ、うまくいきませんでした。模範解答では、100分の3、100分の4と表していました。
(模範解答)
100分の3(x+200)+100分の4=48
という式でした。
100分の96、100分の97の表し方だと解くことは出来ないのでしょうか?ただ私の勘違いだったらすみません。
詳しく教えて欲しいです。
うちださんへ
100分の96、100分の97の表し方でも解くことはできます。
以下、わたしの解答例です。
昨年度の女子の生徒数をx人とすると、
100分の97(x+200) + 100分の96 x = x+200 + x -48
解いて、x=600
よって昨年度の男子の生徒数は600+200=800(人)。
ゆえに今年度の生徒数は
800+600-48=1352
答.1352人
参考になればさいわいです。
復習がんばってください!
ありがとうございます!参考になりました。
ずっとここでつまづいていたので本当に助かりました。
分からないところがあった時はこのブログにいつも助けられています。復習頑張りたいと思います。また分からないところがあったら質問させて下さい!
割合の問題の問1シャツ1枚の定価はいくらかの問題の答は1,000円ではないですか?間違えてたらごめんなさい
答えは4000円になります。
【ヒント】
①シャツ1枚の定価をx円として、「通常2枚買う場合の合計金額」と「特別期間に3枚買う場合の合計金額」をそれぞれ表してみる。
②(特別期間に3枚買う場合)=(通常2枚買う場合)-300 で方程式をつくって解く。
ちなみに、間違えることは自分で考えている証拠なので、すばらしいことだと私は思います。
理解出来ました!
ありがとうございました
いつもながら、たいへん参考になりました。
特に、「<割合>とは、ようするに何倍かってこと。」は新鮮でした。
問3)濃度15%の食塩水150gと、濃度8%の食塩水を混ぜあわせて、10%の食塩水をつくりたい。8%の食塩水を何g 混ぜればいいか。
答.450g
ちょっと!これも答え375gでしょ!
いい加減にして下さいよ
たびたびのご指摘ありがとうございます。
確認して修正しました、すみません。
これを機に全練習問題を再度点検しました。
いい機会をいただきありがとうございました。
すいません、どうしても答えが合わなくてイラっとしてしまいました。
他の問題はこちらの計算間違いでした。
じゅうごさんの説明の仕方はすごくわかりやすくて最近よく使わせてもらっているんです。
本見てわからない所もじゅうごさんのサイトを見て理解できたんです。
なので引き続き利用させて頂きます。
そう言っていただけるとうれしいです。
「アジアの歴史」記事をあとひとつ書き終えたら、また数学指導法の記事を再開する予定ですので、ひきつづき温かく厳しく見守ってやってくださると助かります。
またわからない所あったら質問してもいいですか?
もちろんです。
いつでもお待ちしています。