中学数学「平面図形」のコツ、４回目は図形の移動です。
- 平行移動
- 対称移動
- 回転移動
という３つの移動の性質を、まずわかりやすく振り返ります。
そのあと、よく出る応用問題を５種類、解説していきます。
とくに
「回転移動と点対称移動って何が違うの？」
「回転移動の中心の見つけ方は？」
「移動して重なる問題が苦手…」
こんな中学生は参考にしてください。
[中学数学「平面図形」の記事一覧]
３つの移動を押さえよう
「テトリス」や「ぷよぷよ」など、いわゆる落ちゲーをやったことのある人は多いでしょう。
そういう人も、そうでない人も、平面上で図形を移動させる仕方は３種類あると気づいていることと思います。
そう、それが
- 平行移動
- 対称移動
- 回転移動
の３種類です。
平行移動の性質
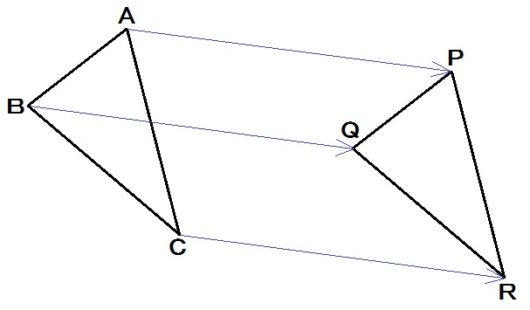
平行移動とは、横にすぅーっとズラす移動の仕方です。
上図でいうと、△ABCをすぅーっとズラして△PQRにする方法。
さて、この平行移動の性質を考えるために、三角形の動いた跡(あと)を描いてみましょう。
ぜんぶ描くとごちゃごちゃするんで、とりあえず３つの頂点A,B,Cが動いた跡だけ描きこんでみました（上図の青線）。
すると、図を見てもらえばわかりますが、線分AP,線分BQ,線分CRは
- 平行で
- 長さが等しい
となってます。
つまり記号で書くと
$$ AP /\!/ BQ /\!/ CR $$
$$ AP = BQ = CR $$
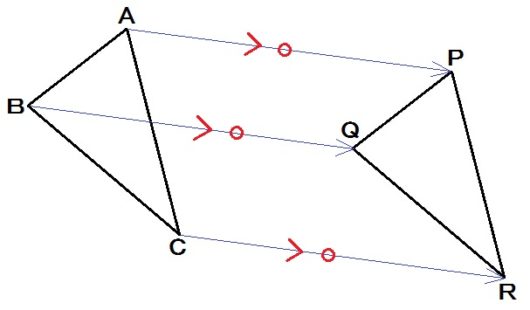
これが平行移動したときの性質になります。
３つの移動のなかではいちばんカンタンですね。
対称移動の性質
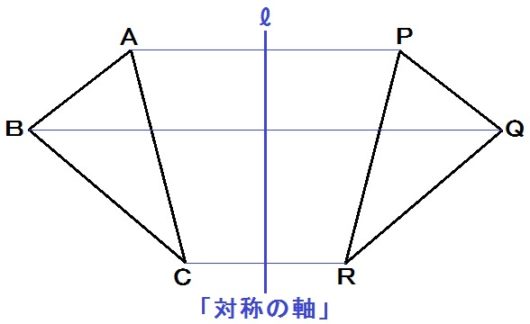
対称移動とは、紙を折って裏返しにする移動のこと。
あるいは鏡写しみたいな移動といってもいいでしょう。
上図でいうと、ℓを折り目として、△ABCを△PQRにペタンと折る移動方法です。
このとき、折り目の線ℓを数学用語で「対称の軸」といいます。
さて、対称移動でも頂点の動いた跡を結んでみました。
すると、線分AP,線分BQ,線分CRについて、
- 線分APの垂直二等分線は？→ℓ
- 線分BQの垂直二等分線は？→ℓ
- 線分CRの垂直二等分線は？→ℓ
ということがわかる。
つまり記号で書くと
$$ A\ell_1 = P\ell_1 \quad B\ell_2 = Q\ell_2 \quad C\ell_3 = R\ell_3 $$
$$ AP \perp \ell \quad BQ \perp \ell \quad CR \perp \ell $$
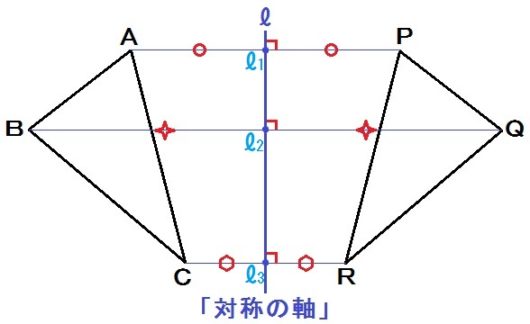
これが対称移動の性質です。
「対称移動では、対応する頂点を結ぶ線分は、対称の軸によって垂直に二等分される」って日本語の意味も、ようするにこれです。
ことば丸覚えじゃなくて、イメージで理解しときましょう。
ちなみに。
小学校で習った線対称移動は、この対称移動とまんま同じです。
つまり線対称移動＝対称移動。
ややっこしいですが、用語を統一してないのはわれわれ大人の不手際です、許してください。
回転移動の性質
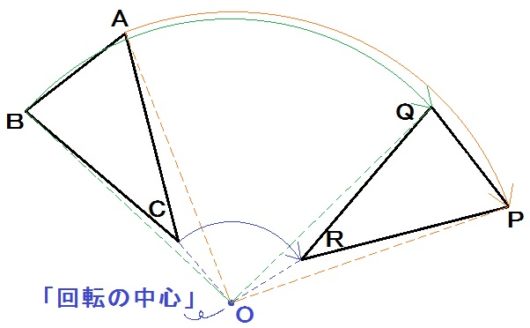
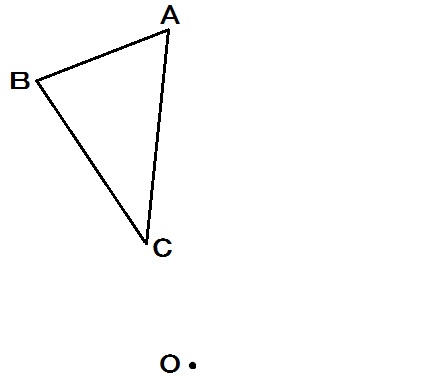
回転移動とは、どっかを中心にしてグルッと回す移動のこと。
上図でいうと、Ｏを中心に△ABCをグルッと回して△PQRにする移動方法です。
このとき、Ｏを数学用語で「回転の中心」といいます。
この回転移動はけっこう自由がきいて、左右どっちに回してもいいし、回す角度も好きに決めていい。
ただやっぱり性質はあるので、頂点の動いた跡をくわしく見てみましょう。
ごちゃごちゃしてるので分けて描くと、おうぎ形（つまり円の一部）が３つできてますね↓
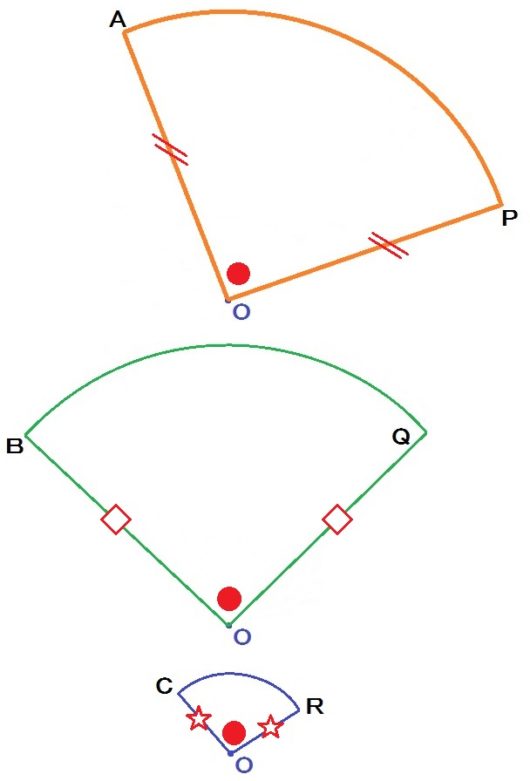
この図から、
$$ OA=OP \quad OB=OQ \quad OC=OR $$
$$ \angle AOP = \angle BOQ = \angle COR $$
これが、回転移動の性質です。
「回転移動だと、おうぎ形（つまり円の一部）ができるし、角度はみんな同じ」と覚えておきましょう。
ちなみに。
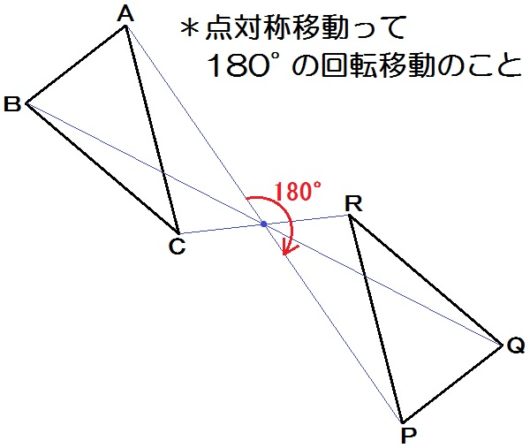
小学校で習った点対称移動は、この回転移動の一部です。
つまり点対称移動＝180°の回転移動。
これで、小学校の知識がぜんぶ中学校とつながりますね。
以上、３種類の移動の性質でした。
ようするにみんな、頂点の動いた跡（これを数学用語で「軌跡」といいます）のことを言ってるだけ。
- 平行移動：平行で長さが等しい
- 対称移動：対称の軸が垂直二等分線になる
- 回転移動：おうぎ形（円の一部）ができて、角度は同じ
これらの性質を利用して、以下、よく出る応用問題を解いていきましょう。
＞Amazonプライム・ビデオで「名探偵コナン シーズン１」を観る
よく出る応用問題
中学数学「平面図形」のうち、図形の移動でよく出る問題は、以下の５パターンです。
- 対称移動の作図
- 対称の軸の作図
- 回転移動の作図
- 回転の中心の作図
- 移動して重なる問題
それぞれ、例題とともに解いていきましょう。
（作図の基本とコツについては前回までの記事を参照）
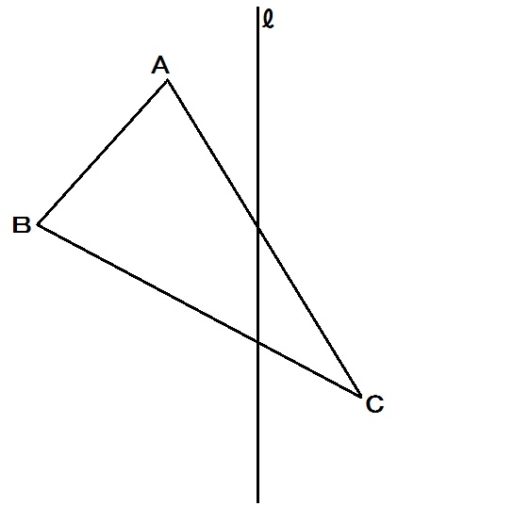
1.対称移動の作図
例題１）次の図で、△ABCを直線ℓについて対称移動させてできる△PQRをかけ。
作図問題のコツのひとつは、まず完成形をイメージすることでした。
そこで出来上がりをラフに描くと、こんなかんじ↓
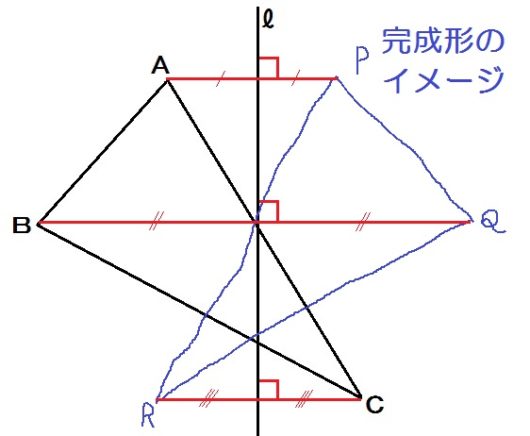
対応する頂点を結んだ線も、かき加えました。
するとわかるでしょう、
AP⊥ℓだし、APのまんなかがℓだと。
これはBPについてもCRについても同様です。
よって、解き方は以下のとおり。
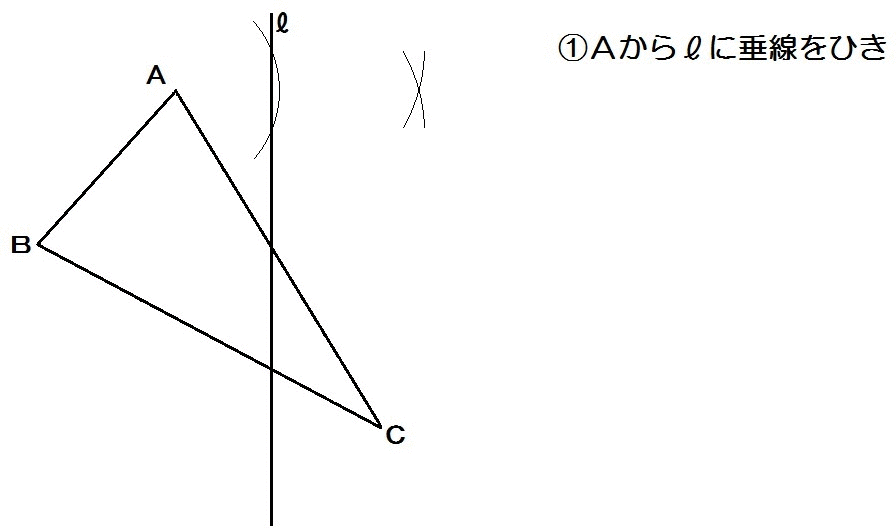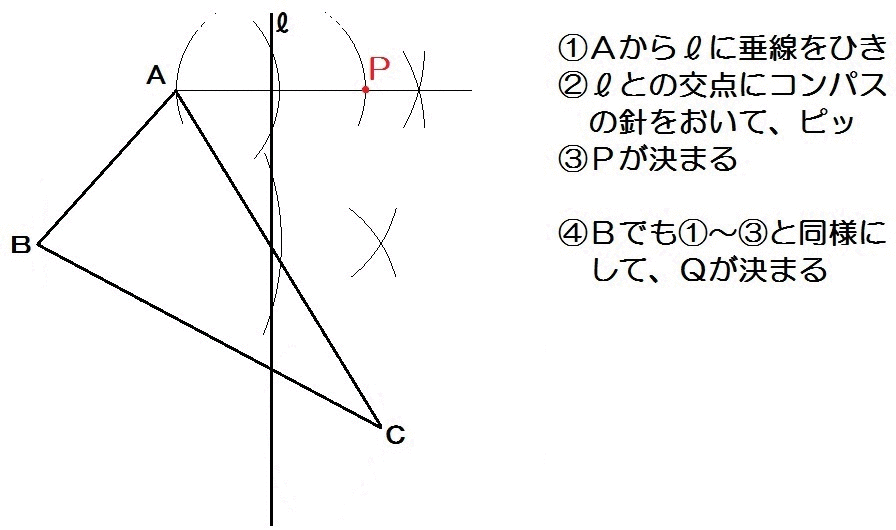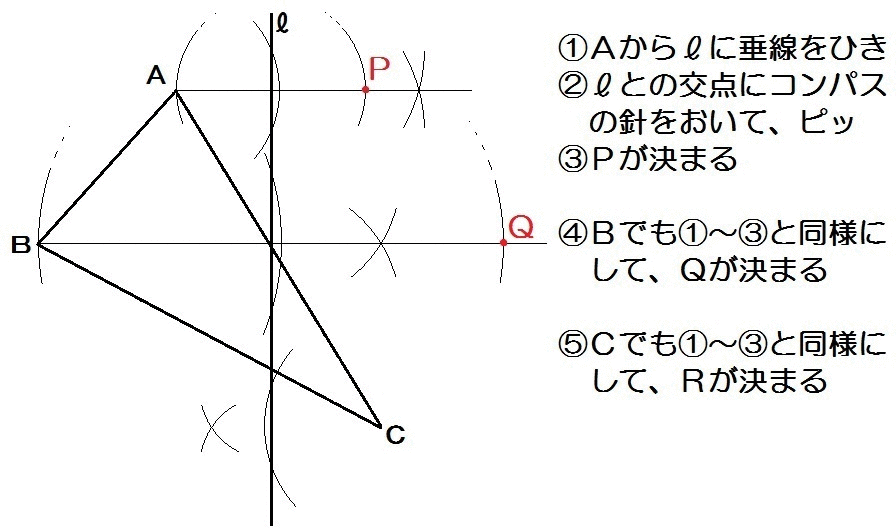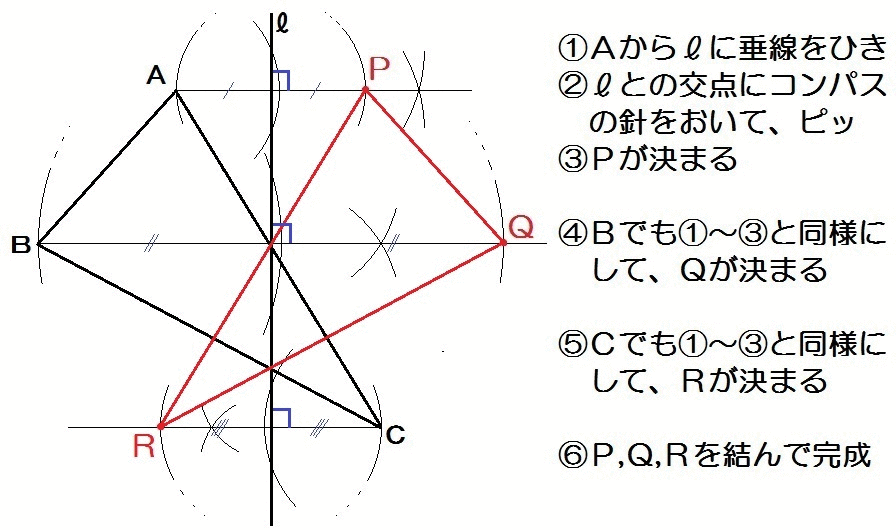
垂線で「垂直」を作図。
そのあとコンパスで「等しい長さ」を作図。
これを各頂点でくりかえす。
これが対称移動の作図になります。
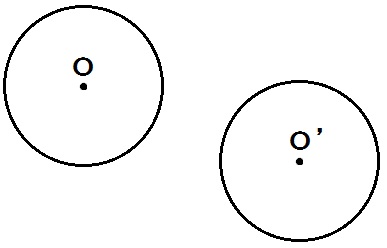
2.対称の軸の作図
例題２）次の図において、円Ｏを対称移動させたところ円Ｏ’になった。このときの対称の軸を作図せよ。
もう描きませんが、中学生のみなさんはまず完成形をイメージしてくださいね。
完成形が描けたら、わかるはず。
対称の軸って、線分OO’の垂直二等分線になってると。
よって、解き方は以下のとおり。
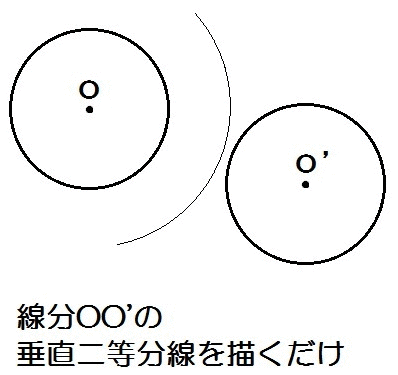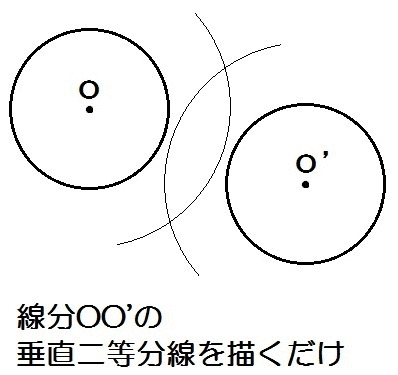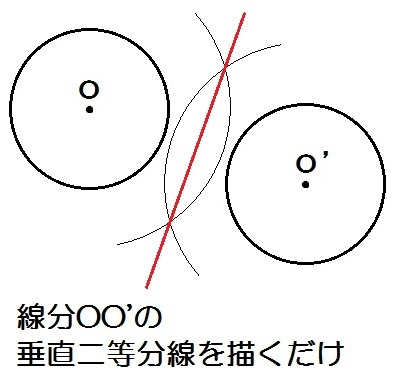
対応する頂点を結んで、その線分の垂直二等分線を描くだけ。
これが対称の軸の作図になります。
3.回転移動の作図
例題３）次の図のような△ABCを、点Oを回転の中心として、時計回りに90°だけ回転させてできる△PQRを作図しなさい。
ただし、分度器を使わないで、定規とコンパスだけを使うこと。
例題３は回転移動の作図です。
まず完成形をイメージしましょう。
もう描かないといったけど、ちょっと難しい問題だから描くと、こんなかんじ↓
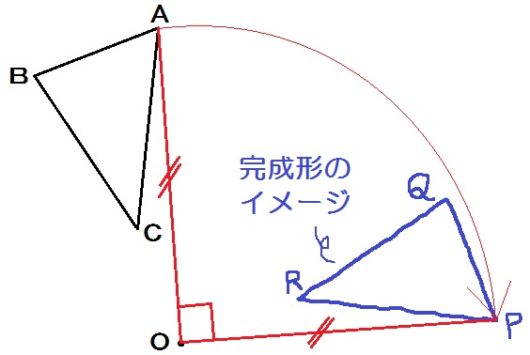
ここで、頂点Ｐを作図するにはどうしたらいいかと考えてみましょう。
Ｐは ∠AOP＝90° , OA=OP のところ。
90°の作図は、そう、垂線が使えます。
よって、解き方は以下のとおり。
垂線で「90°」を作図。
そのあとコンパスで「等しい長さ」を作図。
これを各頂点でくりかえす。
これが回転移動の作図になります。
ちなみに、60°でも30°でも105°でも、前回までの記事を読んでいればできるはず。
分度器を使わないで、コンパスと定規だけでいろんな角度が描けること、あらためて確認しましょう。
[参考記事]
4.回転の中心の作図
例題４）次の図において、直角三角形PQRは、直角三角形ABCを回転移動したものである。
このとき、回転の中心Oを、作図によって求めなさい。
2017年度 大分県公立高校入試問題 1-7
今度は逆に、回転の中心を求める問題です。
このような、回転移動における回転の中心の見つけ方は、高校入試でも頻出。
ぜひこの機会に理解してください。
さて、完成形をイメージしたなら、中心Oは
- ２点A,Pからの距離が等しい
- ２点B,Qからの距離が等しい
- ２点C,Rからの距離が等しい
ところってわかりますね。
点からの距離が等しい…
そう、垂直二等分線です。
よって、解き方は以下のとおり。
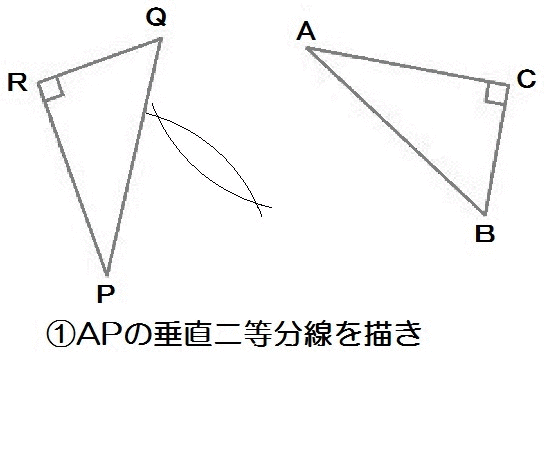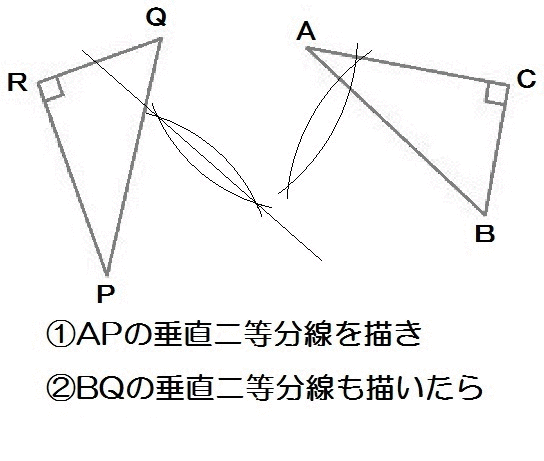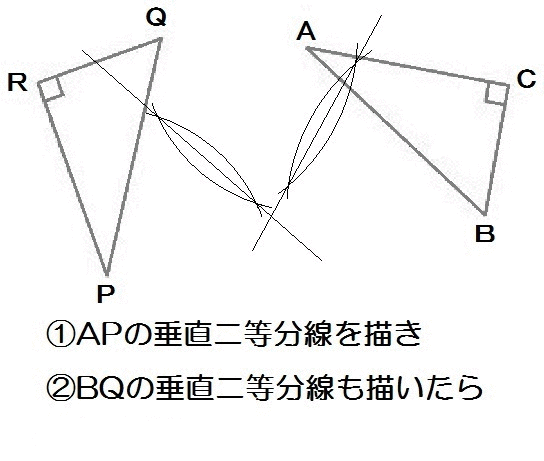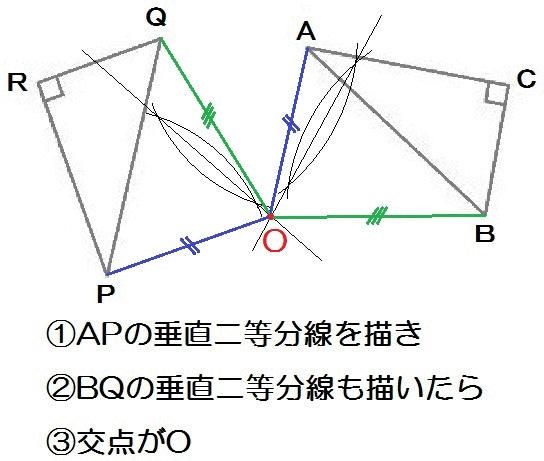
APの垂直二等分線とBQの垂直二等分線の交わるところが、回転の中心Oになります。
もちろんAPとCR、BQとCRの組み合わせでもかまいません。
とにかく、回転移動において、回転の中心の見つけ方は？と聞かれたら
垂直二等分線だということ。
このあたり、円の中心の作図等と考え方は似ています。
[参考記事]
5.移動して重なる問題
例題５）次の図は合同な直角二等辺三角形を組み合わせたものである。
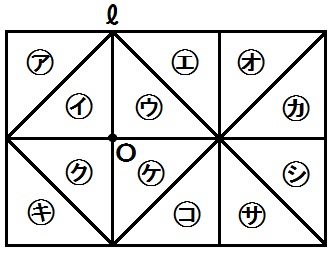
(1)㋐を平行移動して重ねることのできる三角形をすべて答えよ。
(2)㋐を、直線ℓを対称の軸として対称移動し、さらに平行移動して重ねることのできる三角形をすべて答えよ。
(3)㋐を、点Oを回転の中心として180°回転移動し、さらに平行移動して重ねることのできる三角形をすべて答えよ。
最後は、移動して重なる問題です。
それぞれ自力で解いてみてください。
ポイントは
- 平行移動：向きが変わらない
- 対称移動：裏返し
- 180°回転移動（点対称移動）：グルッと反対側
です。
…
……
………
それでは、解答。
(1) ㋔と㋘
(2) ㋗と̪㋛
(3) ㋑と㋕
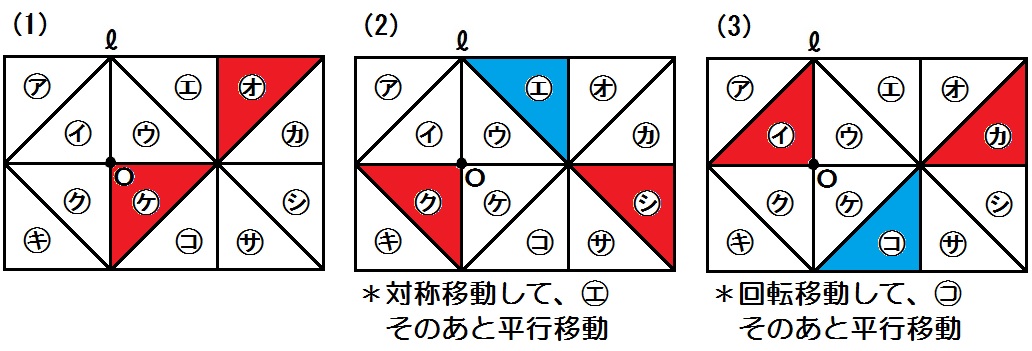
この「移動して重なる」問題が苦手という中学生は、じっさいに㋐の形の三角形を紙でつくって、すぅーっとズラしたり、裏返したり、グルッと回したりしてみましょう。
手を使うという手間を惜しまないこと。
図形問題でとっても大切なコツのひとつです。
以上、よく出る応用問題５種類でした。
質問や疑問があればコメント欄からどうぞ。
＞Amazonプライム・ビデオ「映画 それいけ！アンパンマン たのしくてあそび ママになったコキンちゃん！？」
まとめ
中学数学「平面図形」における図形の移動は、３種類。
- 平行移動：平行で長さが等しい
- 対称移動：対称の軸が垂直二等分線になる
- 回転移動：おうぎ形（円の一部）ができて、角度は同じ
よく出る応用問題は、以下の５つ。
- 対称移動の作図
→垂線で「垂直」を、コンパスで「等しい長さ」を作図。 - 対称の軸の作図
→垂直二等分線を描くだけ。 - 回転移動の作図
→角度を作図して、そのあとコンパスで「等しい長さ」を作図。 - 回転の中心の作図
→垂直二等分線を２本。 - 移動して重なる問題
→苦手な人は紙でつくってみること。
おつかれさまでした。
次回は平面図形のラスト、「円とおうぎ形」をやっつけます。
とくにおうぎ形問題のコツをくわしく解説する予定。
中心角・弧の長さ・面積と、それぞれの公式を覚えているような中学生は、すぐに次の記事を読んでそれをやめてください。
公式など覚えなくても、おうぎ形は解けるんです。
[中学数学「平面図形」の記事一覧]
コメント
いつもありがとうございます。
作図による移動だけでなく、
マス目上で移動させる問題もあるといいかな、
と思いました。