つづいて角度の問題を4つ、
円の問題を3つ出題します。
角度の問題
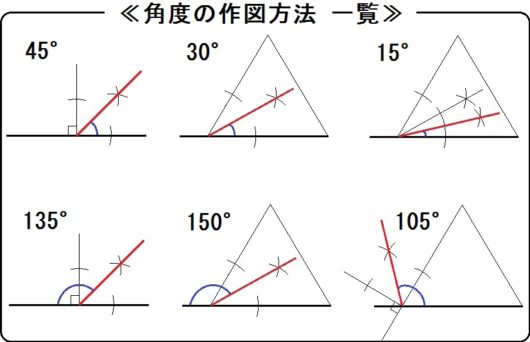
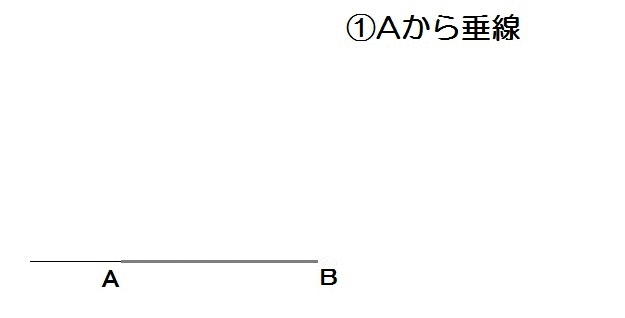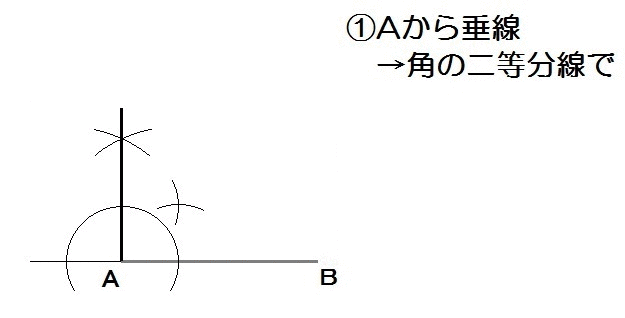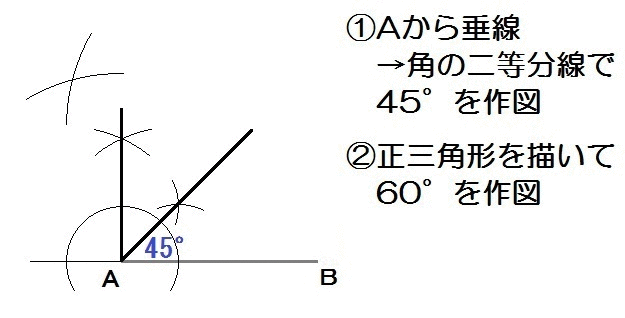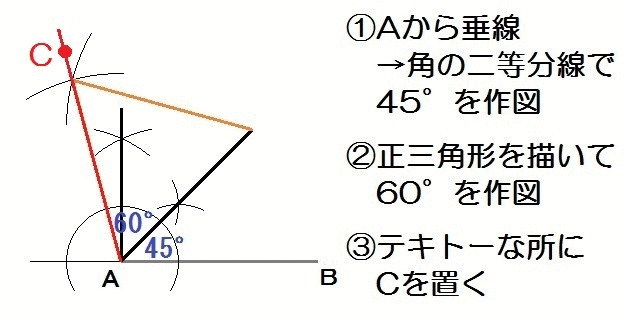
2回目の記事で学習したとおり、角度の作図方法はこれら↑でした。
加えて、90°は垂線、60°は正三角形でしたね。
確認できたら、いざ、入試問題にいきましょう。
福井県 入試問題(2018)
問4)右図のように、直線ℓ、mがある。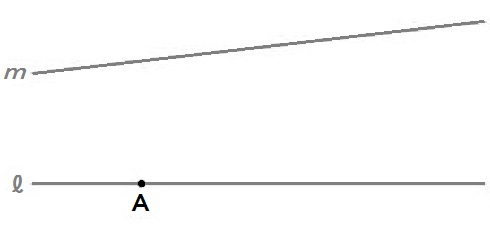
点Aが直線ℓ上にあるとき、
以下の3つの条件にあてはまる△ABCを作図せよ。
(作図に用いた線は消さないこと。)
【条件】
・点Bは直線m上にある。
・点Cは直線ℓ上にあり、点Aの右の方にある。
・∠BAC=90°であり、∠ABC=60°である。
2018年度 福井県 公立高校入試問題A 1-6
【ヒント】
- まずは完成形をイメージして書いてみよう
- 完成形さえわかれば、90°と60°の作図は簡単
…
……
それでは解き方です。
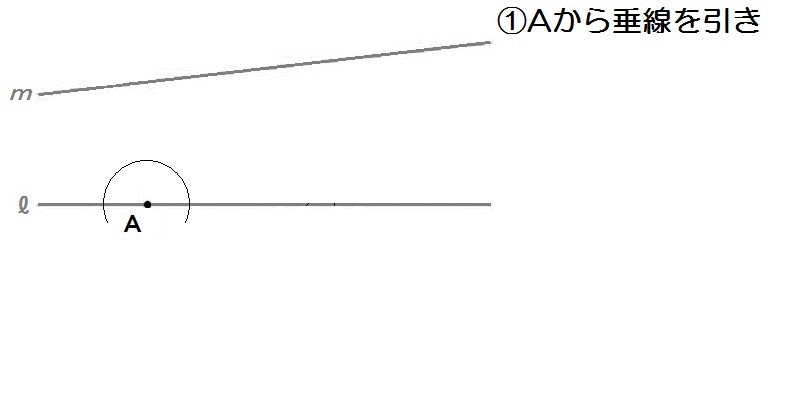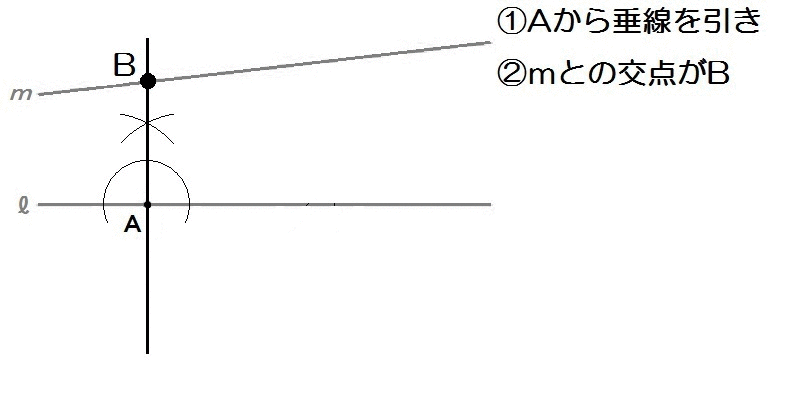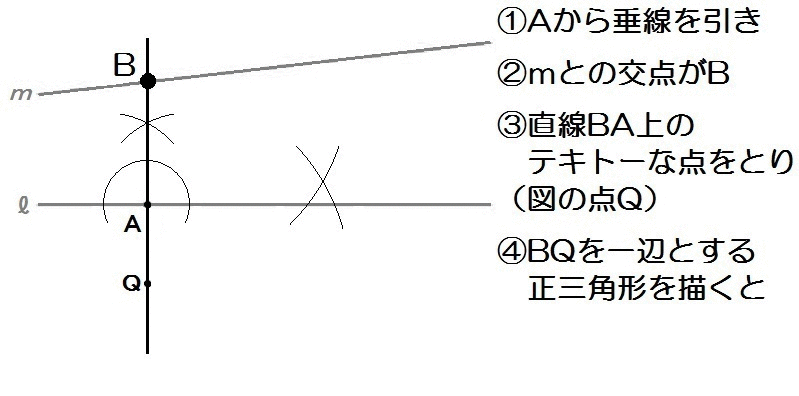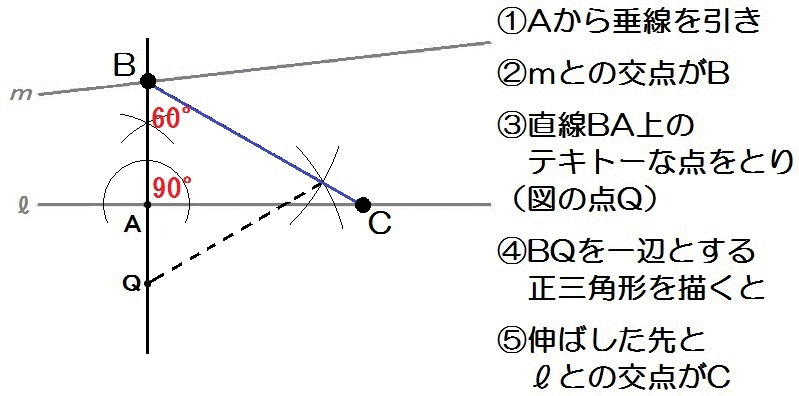
点Aから垂線を描いて90°。
んで∠Bをもつ正三角形を描いて60°ですね。
実はこれは1回目の記事で、完成形をイメージするのがいかに大切か、その例として挙げた問題です。
この問題でつまずくという中学生は、まず完成形をイメージして書くというコツを、この機会に身につけてください。
なお、後半は別の解き方もありますが、中1の範囲ではないので割愛します。
埼玉県 入試問題(2019)

∠CAB=105°となる半直線ACを
コンパスと定規を使って1つ作図しなさい。
ただし、作図するためにかいた線は、消さないでおきなさい。
2019年度 埼玉県 公立高校入試問題 2-3
【ヒント】
- 完成形をイメージしてから
- 105°を作るには?
- 半直線ACに注意して
…
……
それでは解き方です。
この解答例では「45°→60°」の順で作図しましたが、「60°→45°」の順でもかまいません。
また60°を半分のさらに半分にして15°を作り、90°と合わせても、あるいは120°から引いても、OKです。
つまり105°の作図には
- 45°+60°
- 60°+45°
- 90°+15°
- 15°+90°
- 120°-15°
の計5パターンあるってことですね。
千葉県 入試問題(2018後期)
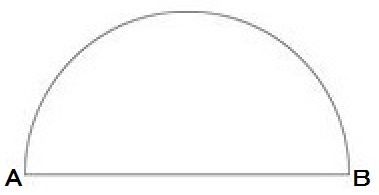
線分ABの中点をOとし、弧AB上に点Pをとり、∠POB=30°となる線分OPを作図によって求めなさい。
また、2点の位置を示すO,Pも書きなさい。
ただし、三角定規の角を利用して直線をひくことはしないものとし、作図に用いた線は消さずに残しておくこと。
2018年度 千葉県 公立高校入試問題(後期) 2-5
【ヒント】
- まず中点Oを作図
- 30°を描くには?
…
……
それでは解き方です。
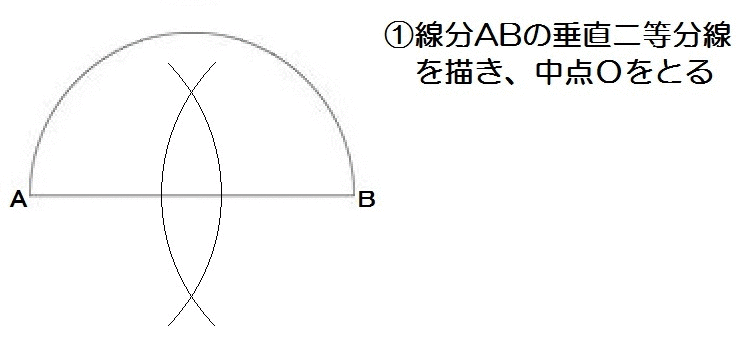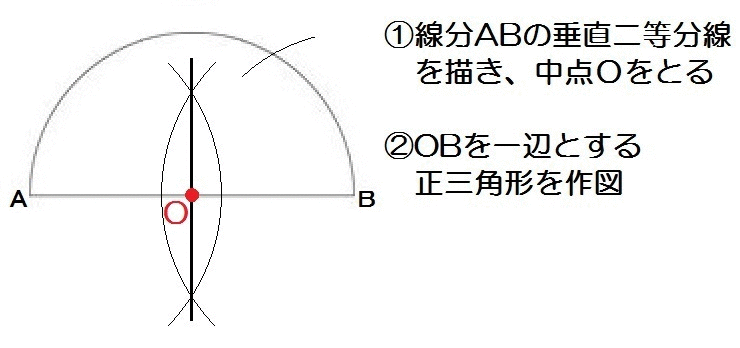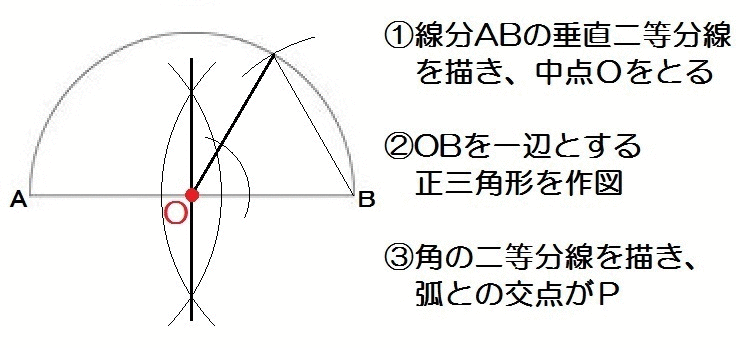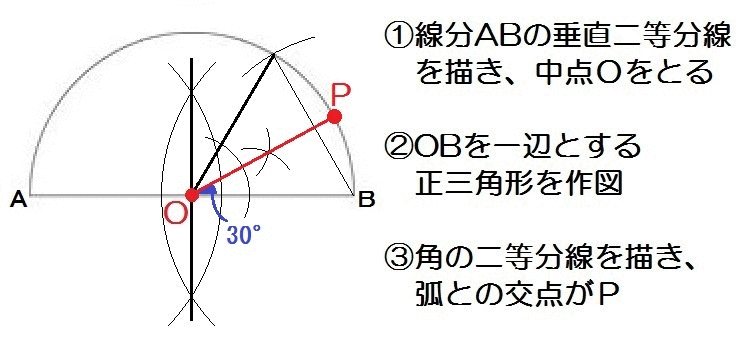
垂直二等分線、正三角形、角の二等分線のあわせ技ですね。
ちなみに手順②において正三角形を作図するには、中心B,半径BOでコンパスをピッとやれば、弧との交点がもう正三角形の頂点になります。
(なぜかって?じっさいに描いてみたらわかります)
福井県 入試問題(2019)
【ヒント】
- なにはともあれ完成形をイメージ
- まず45°を作図して
- ひし形=長さがぜんぶ等しい四角形
…
……
それでは解き方です。
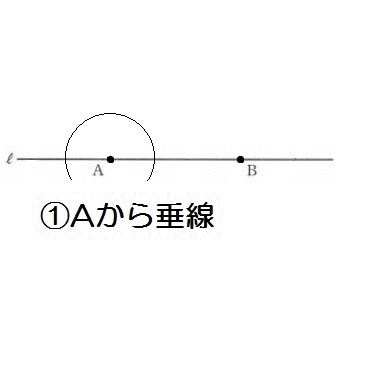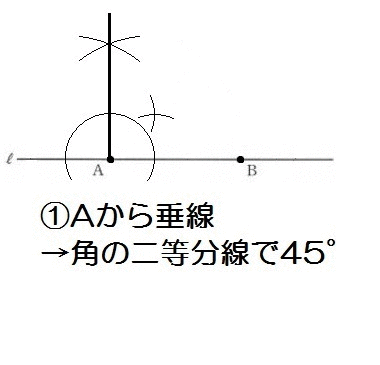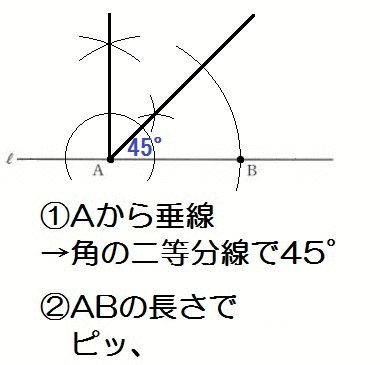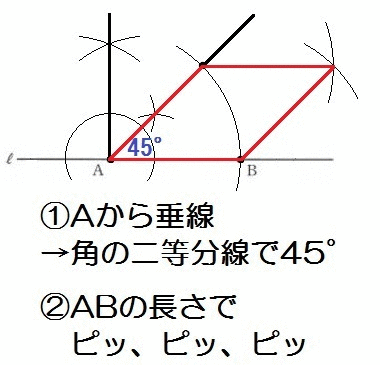
45°の作図のあと、ABの長さにコンパスを合わせて交わらせていけば、ひし形の頂点がひとつずつ決まっていきますね。
以上、角度の問題4つでした。
ちなみに福井県は2年連続で角度の作図問題が出ました。2020年度はどうなんだろう?
円の問題
高校入試では円にかんする作図問題もよく出題されます。
その中から3つ、選りすぐってみました。
北海道 入試問題(2018)

円Oの円周上に点Pをとり、△ABPの面積がもっとも小さくなるようにします。
点Pを定規とコンパスを使って作図しなさい。
ただし、点を示す記号Pをかき入れ、作図に用いた線は消さないこと。
2018年度 北海道 公立高校入試問題 2-3
【ヒント】
- 三角形の面積=底辺×高さ× \(\frac{1}{2}\)
- 底辺ABは決まってるから、高さがもっとも短くなるトコロがP
- 点と直線の最短距離も参照
…
……
それでは解き方です。
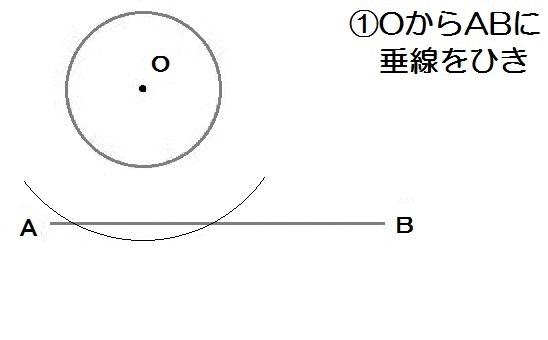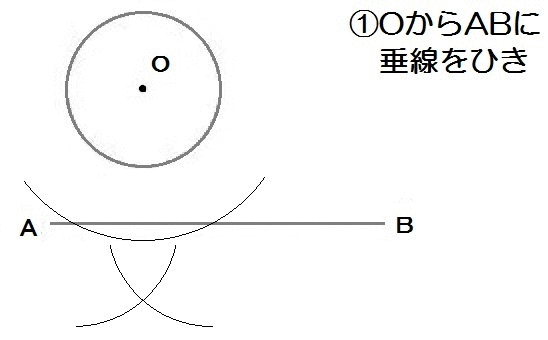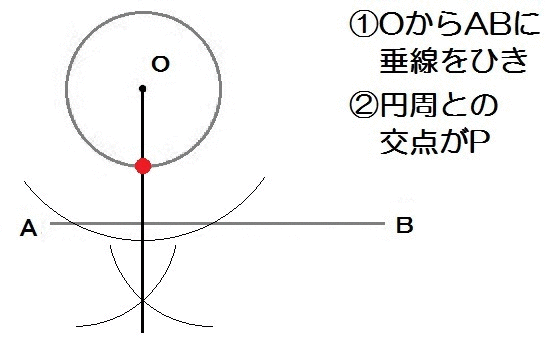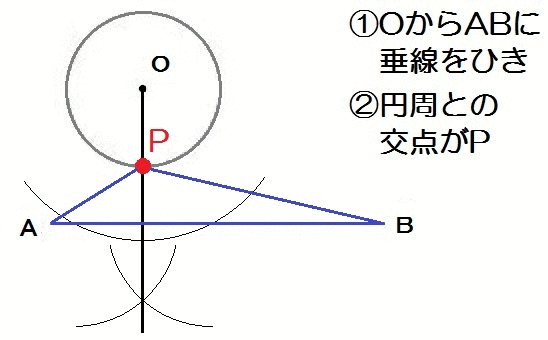
高さが最短→直線ABとの最短距離→垂線ということ。
「点と直線の最短距離」のリンクにもありますが、前回の記事で2018群馬(後期)の過去問を解いていれば、かんたんですね。
静岡県 入試問題(2019)
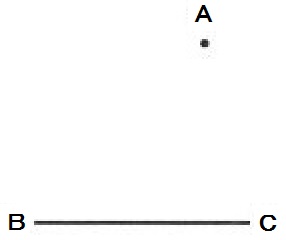
点Aを通り、線分BCが弦となる円の中心Oを作図しなさい。
ただし、作図には定規とコンパスを使用し、作図に用いた線は残しておくこと。
2019年度 静岡県 公立高校入試問題 2-1
【ヒント】
- 「弦」とはこんなやつ↓
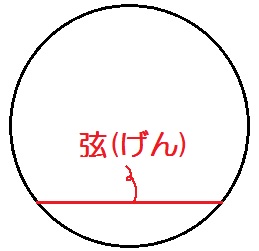
…
……
それでは解き方です。
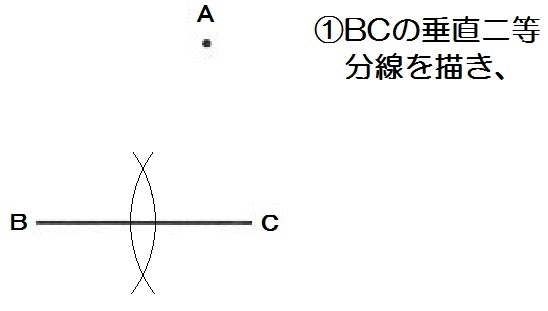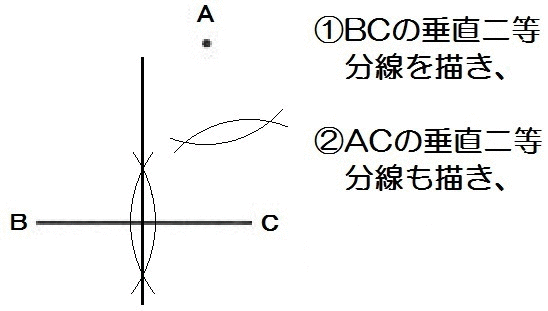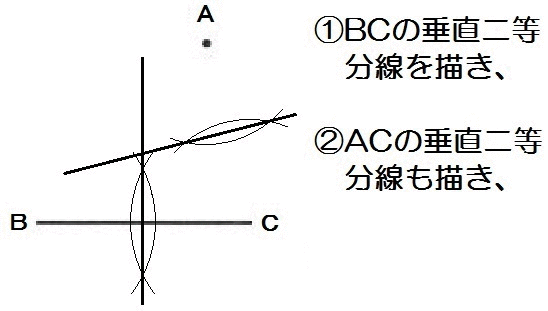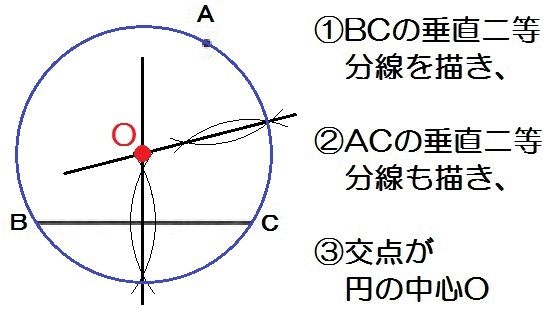
つまり3点A,B,Cを通る円の中心を作図すればいいので、垂直二等分線を2本、なわけです。
解答例ではBCとACの垂直二等分線ですが、もちろん他の組み合わせでもかまいません。
前々回の記事で、垂直二等分線の特徴の応用範囲として、
- 点からの距離が等しい(北海道2019)
- 円の中心(兵庫2019)
- 三角形の外接円(富山2019)
とやりましたね。
これらの問題といっしょ。
ただ聞き方が変えてあるだけ。
ということを、完成形をまず描いていたら気づくはずです。
栃木県 入試問題(2018)
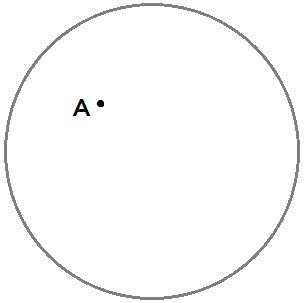
円周上にある点のうち、点Aとの距離が最も長い点Pを作図によって求めなさい。
ただし、作図には定規とコンパスを使い、また、作図に用いた線は消さないこと。
2018年度 栃木県 公立高校入試問題 2-1
【ヒント】
- 線分APはどこを通る?
…
……
それでは解き方です。

Aからもっとも遠い円周上の点は、Aと中心を結んだ先にある。
よって、円の中心を垂直二等分線2本で求めることになります。
ちょっと難問ですが、自分で描いた完成形とヒントを参考にしたら、解けたという中学生も多いはず。
作図問題はまず完成形をイメージする、このコツを忘れずに。
では最後に、力試し問題です。




コメント
2つ目の問題で、なぜ外側の点なのでしょうか?
条件②に「点Pは、直線ABと直線BCから等しい距離にあり、△ABCの外部の点である」とあるためです。
前回同様ですが、
栃木県 入試問題(2018)で、
・Aからもっとも遠い円周上の点は、Aと中心を結んだ先にある
の理由がよくわかりません。
直感的には、それしかないな、とわかるのですが。