高校入試の作図問題、ラストは力試しを2つ出題します。
力試し問題
以下の2問はそこそこ難問です。
これがノーヒントで解けたら、作図問題はバッチリだと自信をもっていいでしょう。
ってことで、ヒントなしでどうぞ。
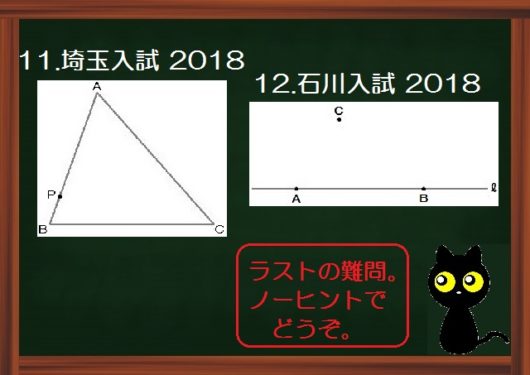
埼玉県 入試問題(2018)
点Pを通る直線を折り目として、点Aが辺BCに重なるように△ABCを折ります。
このとき、折り目となる直線をコンパスと定規を使って作図しなさい。
ただし、作図するためにかいた線は、消さないでおきなさい。
2018年度 埼玉県 公立高校入試問題A 2-3
(ヒントがほしい人は以下をドラッグ反転)
- 完成形において、点Aが辺BCと重なった点をA’とすると、AP=A’Pとなる
- よってA’がまず作図できる
- あとは「点Aと点A’が重なるときの折り目」を描けばいい
- これ、垂直二等分線の応用範囲のひとつ
…
……
それでは解き方です。
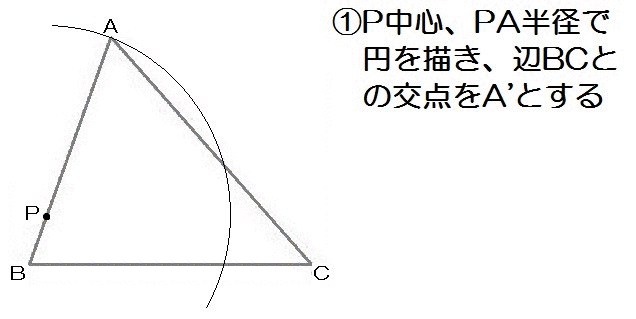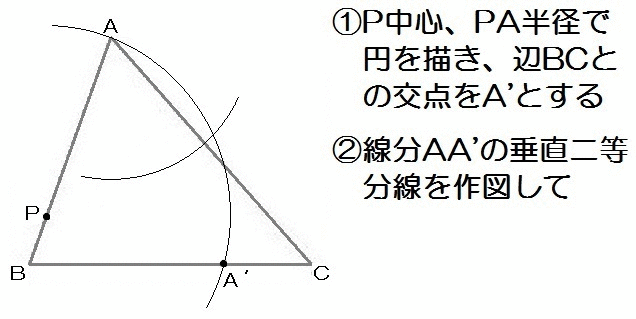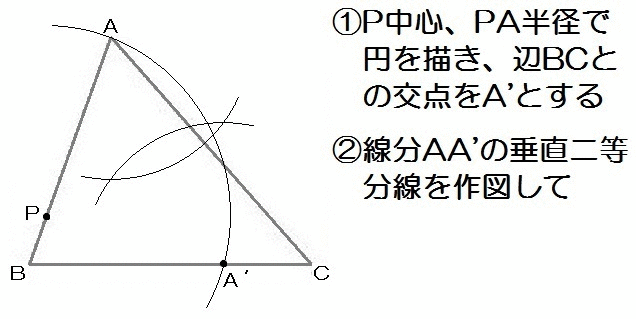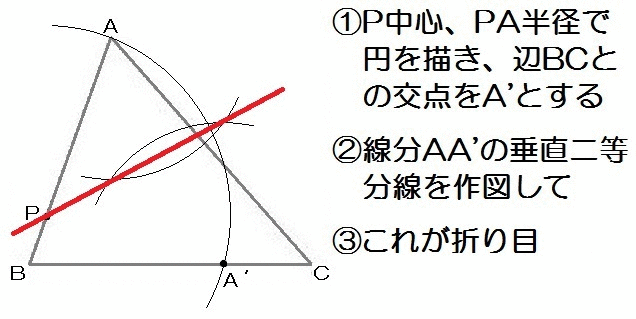
完成形をイメージすると、AP=A’Pとなるから、Pに針をおいてコンパスでA’を作図。
んで点どうし(AとA’)が重なるときの折り目だから、垂直二等分線をひきます。
点どうしが重なるときの折り目という応用範囲、前々回の記事でやりましたね。
また、平面図形を折る問題のコツとして
「折る前と折った後の、辺や角は等しい」
というのがありました。
これも前回の辺どうしが重なるときの折り目でやりましたね。
こうしたいろんな知識が頭に整理されていれば、高校入試の難問にも立ち向かえます。
すぐできなくてもかまいません。
3回分の記事を参照しながら、たくさん問題を解いて、すこしずつ身につけていってください。
ちなみにこの問11の後半は「Pから辺AA’に垂線をひく」という解き方でもOKです。
[作図の記事一覧]
石川県 入試問題(2018)
問12)2点A,Bを通る直線ℓと、ℓ上にない点Cがある。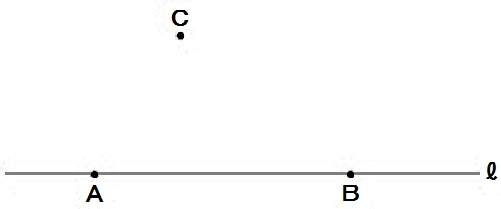
これを用いて、次の条件①~③をすべて満たす点Pを作図しなさい。
ただし、作図に用いた線は消さないこと。
【条件】
①点Pは、直線ℓに対して点Cと同じ側にある。
②PB⊥ℓ
③△PABの面積は、△CABの面積の \(\frac{1}{2}\) である。
2018年度 石川県 公立高校入試問題 5
(ヒントがほしい人は以下をドラッグ反転)
- まず完成形を描いてみる
- 三角形の面積=底辺×高さ× \(\frac{1}{2}\)
- 底辺は共通だから、高さが半分になればいい
…
……
それでは解き方です。
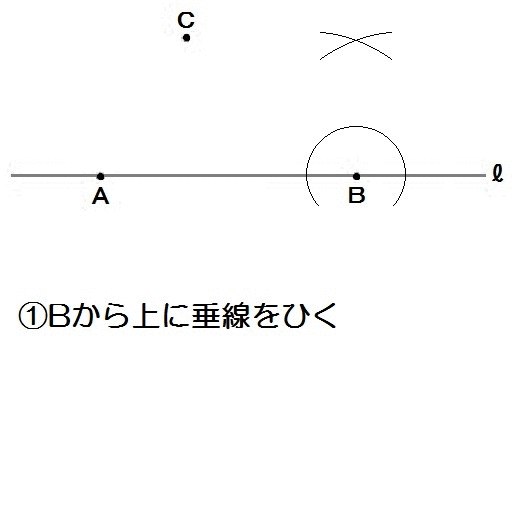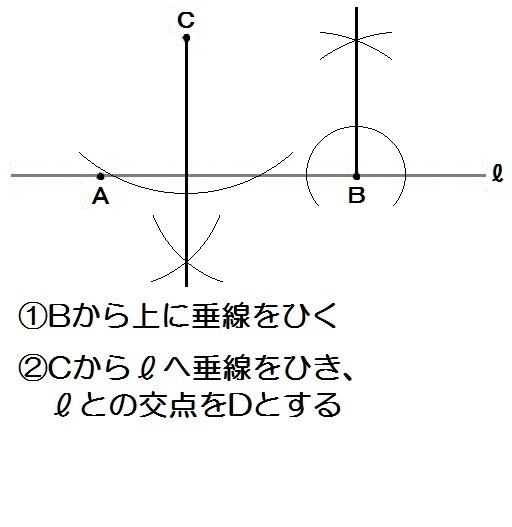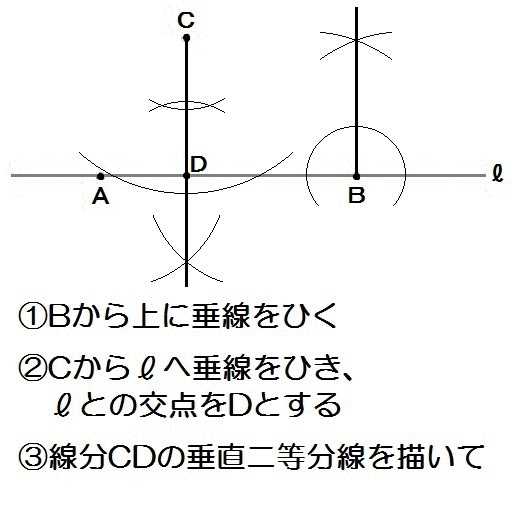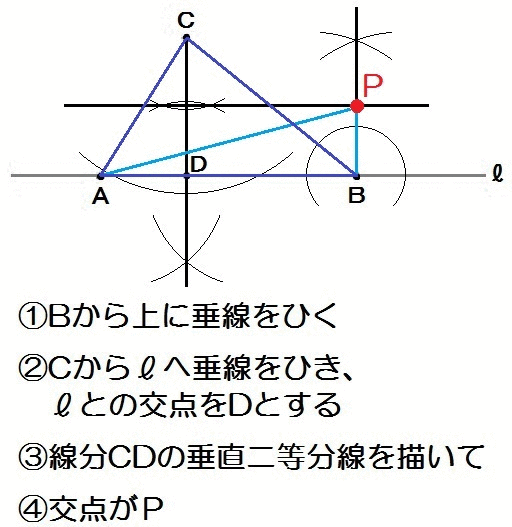
まず条件①②より、Bから垂線を描きます。
次に△CABの高さを作図して、その半分の長さを、垂直二等分線で描きます。
三角形の面積と底辺・高さとの関係は、中学3年生「相似な図形」でくわしくやりますが、中1でもこの石川入試過去問が解けたら、作図問題はバッチリです。
最後に

おつかれさまでした。
高校入試問題12コ、いかがでしたか?
これにて、中学1年生の知識で解ける作図問題はすべて紹介しました。
つまり、作図のコツおよび解き方はぜんぶ伝えました。
あとは練習あるのみ。
たくさん問題を解いて「わかる」を「できる」に変えていってください。
ちなみに、なぜ作図問題では定規とコンパスだけを使うのか?
分度器や三角定規の角を使っちゃダメなのか?
これ、古代ギリシアの伝統です。
古代ギリシア人は定規とコンパスだけを使ってあらゆる図形を描こうという、ヘンテコな趣味をもってました。
それが現代まで続いてるわけです。
以前のコラムでも書きましたが、数学という学問は古代ギリシアの伝統をかなり受け継いでますね。
[参考記事]
数学の証明ってなに?なんで証明するの?なぜ文字を使うの?
閑話休題。
次回は「図形の移動」を解説します。
NEXT→中学数学「平面図形」のコツ④ 図形の移動
[中学数学「平面図形」の記事一覧]
- 垂直二等分線を使った作図
- 角の二等分線、垂線、正三角形を使った作図
- 作図の高校入試問題を解いてみよう
- 図形の移動
- 円とおうぎ形



コメント
2つ目の問題で、なぜ外側の点なのでしょうか?
条件②に「点Pは、直線ABと直線BCから等しい距離にあり、△ABCの外部の点である」とあるためです。
前回同様ですが、
栃木県 入試問題(2018)で、
・Aからもっとも遠い円周上の点は、Aと中心を結んだ先にある
の理由がよくわかりません。
直感的には、それしかないな、とわかるのですが。