つづいて、切断された立体の体積の求め方を解説します。
切断された立体の体積
複雑な図形を攻略するコツは、このブログでずっと言っているとおり、以下2つのどっちかを使うことです。
- 分けて、たす
- 大きく求めて、ひく
ななめに切断した立体
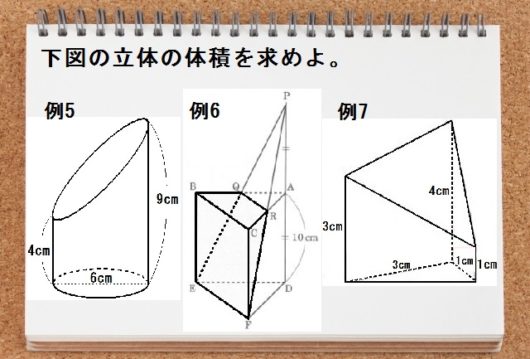
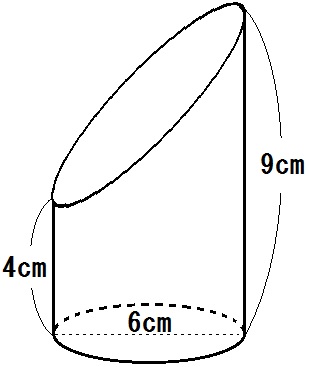
たとえばこんな、円柱をななめに切断した立体の体積を求めてみましょう。
まず「分けて、たす」方法なら、どこで分けるか?
そう、上下に分けたらいいですね。
よって求め方は以下のとおり。
\begin{eqnarray} & & \mbox{(直径6cm、高さ4cmの円柱)} \ + \ \mbox{(直径6cm、高さ5cmの円柱の半分)} \\ &=& 3 \times 3 \times \pi \times 4 \ + \ 3 \times 3 \times \pi \times 5 \times \frac{1}{2} \\ &=& 36 \pi \ + \ \frac{45}{2} \pi \\ &=& \frac{117}{2} \pi \end{eqnarray}
後半は円柱の半分なので、\( \times \frac{1}{2}\) するのを忘れないように。
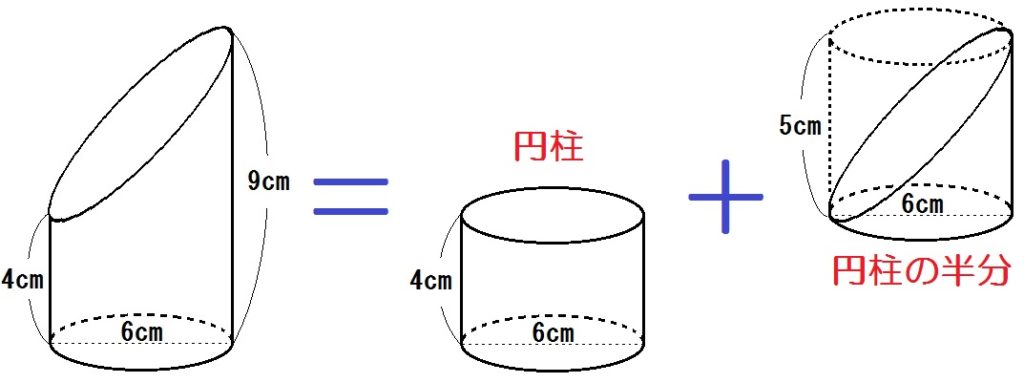
また「大きく求めて、ひく」方法なら?
そう、大きな円柱を求めて、そこから上の円柱の半分を引けばいいですね。
よって求め方は以下のとおり。
\begin{eqnarray} & & \mbox{(直径6cm、高さ9cmの円柱)} \ – \ \mbox{(直径6cm、高さ5cmの円柱の半分)} \\ &=& 3 \times 3 \times \pi \times 9 \ – \ 3 \times 3 \times \pi \times 5 \times \frac{1}{2} \\ &=& 81 \pi \ – \ \frac{45}{2} \pi \\ &=& \frac{117}{2} \pi \end{eqnarray}
いずれにしても答えは \(\frac{117}{2} \pi \) ㎤と出ます。
このように、切断されて複雑になった立体の体積を求めるには、
- 分けて、たす
- 大きく求めて、ひく
のどっちかを使う。
そうすれば、入試問題のような難問でも解いていくことができます。
[その他の複雑な図形の記事]
徳島県入試問題から
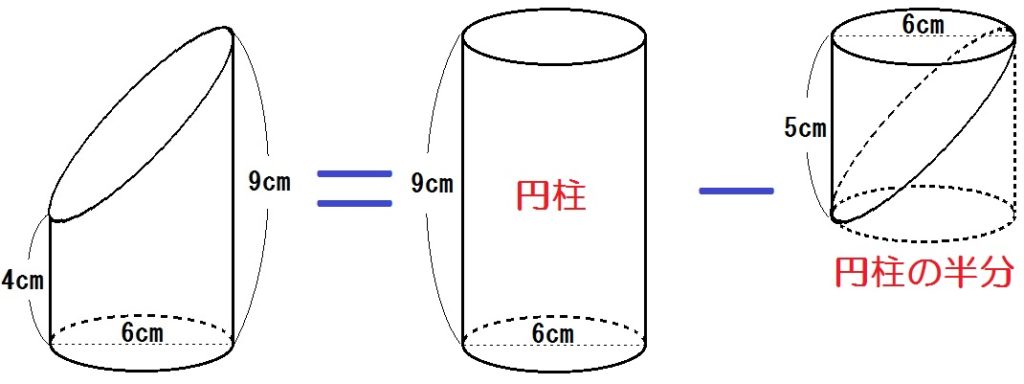
例題6)図1のように1辺の長さが10cmの立方体を、底面の対角線BC,EFを通る平面で半分に切り取ってできた三角柱ABCDEFがある。
図2のように、辺DAの延長上に、DA=APとなるように点Pをとり、線分PEと辺ABとの交点をQ、線分PFと辺ACとの交点をRとする(AQ=AR=5cmとなる)。
また、三角柱ABCDEFが平面QEFRで分けられる2つの部分のうち、頂点Bを含む方を立体Xとする。立体Xの体積を求めなさい。
2019年度 徳島県公立高校入試問題 2-3-b
では力試しとして、2019年度の徳島県公立高校入試問題を解いてみましょう。
問題文が長すぎてイヤになる?
ようするに、この立体の体積を求めよって言ってます↓
この立体Xは三角柱でもないですね。名前のない複雑な立体です。
よって「分けて、たす」か「大きく求めて、ひく」を使います。
どっちがいいか、いろいろと試行錯誤してみてください。
そうしたらやがて気づくでしょう、「大きく求めて、ひく」を2回使えばいいんだと。
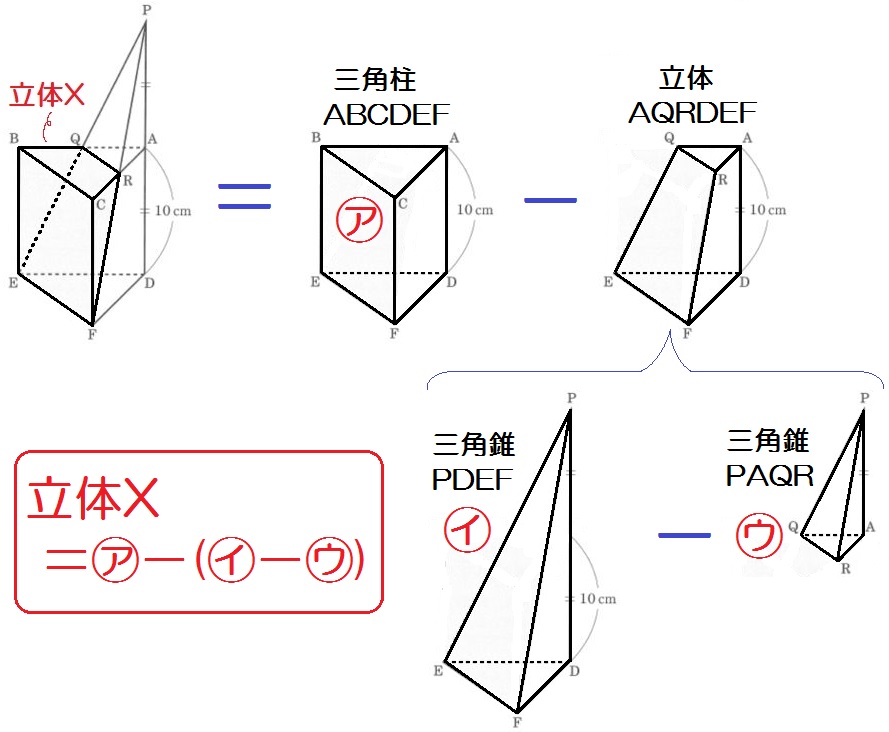
この求め方に気づけば、あとは計算するだけです。
わかりやすいように分けて書くと、
\begin{eqnarray} \mbox{三角柱ABCDEF} &=& 10 \times 10 \times \frac{1}{2} \times 10 \\ &=& 500 \ \mbox{…㋐} \\ \mbox{三角錐PDEF} &=& 10 \times 10 \times \frac{1}{2} \times 20 \times \frac{1}{3} \\ &=& \frac{1000}{3} \ \mbox{…㋑} \\ \mbox{三角錐PAQR} &=& 5 \times 5 \times \frac{1}{2} \times 10 \times \frac{1}{3} \\ &=& \frac{125}{3} \ \mbox{…㋒} \end{eqnarray}
\begin{eqnarray} \mbox{よって、立体X} &=& \mbox{㋐ー(㋑ー㋒)} \\ &=& 500 \ – \ \left( \frac{1000}{3} – \frac{125}{3} \right) \\ &=& 500 \ – \ \frac{875}{3} \\ &=& \frac{625}{3} \end{eqnarray}
答.\( \frac{625}{3} \) ㎤
このように、「分けてたす」「大きく求めてひく」で一発で求まらない場合は、さらに図形を分割して考える。
これが、徳島入試のような難問を解くコツです。
石川県入試問題から
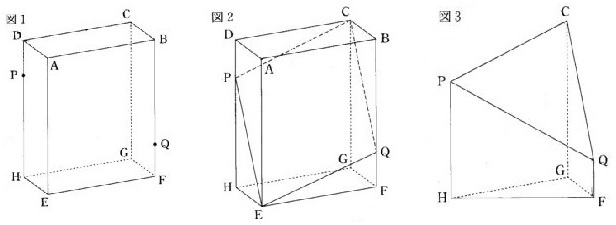
例題7)図1のように、AB=3cm,AD=1cm,AE=4cmの直方体ABCD-EFGHがある。辺DH上、辺BF上にそれぞれDP=QF=1cmとなる点P,Qをとる。
図2のように、4点C,P,E,Qを通る平面でこの直方体を切断し、さらに図3のように、4点P,H,F,Qを通る平面で切断した。
図3の立体CPQ-GHFの体積を求めなさい。
2019年度 石川県公立高校入試問題 7-3
では、力試しをもう1問。
例題7は、昨年度の石川県公立高校入試の最終問題です。
図3の立体、どのようにしたら求まるでしょうか?
…。
そう、「分けてたす」方法でいけますね。
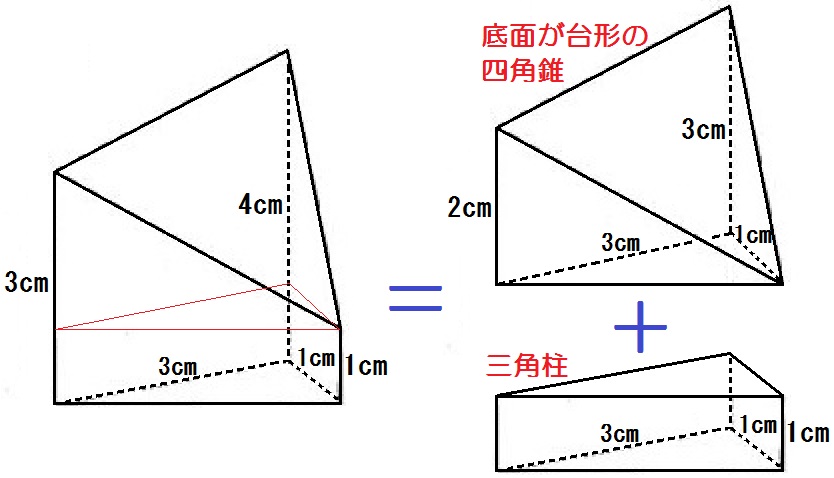
解答は以下のとおり。
\begin{eqnarray} \mbox{四角錐} &=& (2+3) \times 3 \times \frac{1}{2} \times 1 \times \frac{1}{3} \\ &=& \frac{5}{2} \\ \mbox{三角柱} &=& 3 \times 1 \times \frac{1}{2} \times 1 \\ &=& \frac{3}{2} \end{eqnarray}
\begin{eqnarray} \mbox{よって、図3の立体} &=& \frac{5}{2} + \frac{3}{2} \\ &=& 4 \end{eqnarray}
答.4㎤
以上のように、「分けてたす」「大きく求めてひく」を使いこなせれば、入試問題の難問にも太刀打ちできるのです。
練習問題
ここまで、切断された立体の体積を求めてきました。
とくに入試問題を2つ解いてみて、こう思った方もいるでしょう。
「分けてたす」と「大きく求めてひく」、どっちを使うかの判断ができない、と。
もっともな疑問です。
そして判断する方法というのもあります。
しかしそれを書き出すとひじょーに長くなるのでここでは伝えません。
数学は習うより慣れろ。
ここで伝えたコツを土台にして、あとは100問くらい解かせてください。
そうすればおのずとポイントが身につきます。
そして、人から教わるんじゃなくそうやって自分で身につけた解法は絶対に忘れない。
だから生徒にはたくさん練習問題を解かせましょう。
ここでは3問しか載せられませんが、ぜひ参考書や問題集などを使って「わかる」から「できる」へ生徒を導いていただきたいと思います。
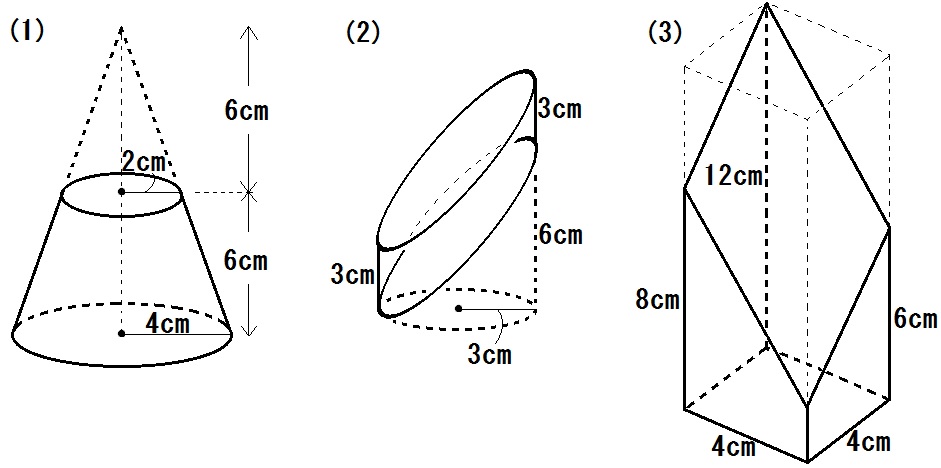
問2)下図の立体の体積をそれぞれ求めよ。
*(3)は前ページで習った「切り口の図形」との合わせ技です。わからないときはコメント欄から質問ください。
解答
(1) \(56 \pi\) ㎠
(2) \(27 \pi\) ㎠
(3) \(112\) ㎠
まとめ

切り口の図形をかくコツは、以下3つのルールに沿って描いていくこと。
- 同じ面上の2点は結ぶ
- 平行な面の切り口は平行になる
- 面を延ばす
切断された立体の体積を求めるには、以下2つのどっちかを使うこと。
- 分けて、たす
- 大きく求めて、ひく
以上!
[空間図形の記事一覧]
- 空間図形① 苦手になる原因と解決方法
- 空間図形② 位置関係・展開図・回転体のコツ
- 空間図形③ 体積のコツ
- 空間図形④ 表面積のコツ
- 空間図形⑤ 立体の切断問題のコツ
さて、次回からは中1数学さいごの単元「データの活用」をお届けします。
→






コメント
例題7や最後の(3)のような問題は、
上記の解き方を理解した上で、
底面積×平均の高さ、
も知っていた方がよいかな、と思いました。
参考になりました。ありがとうございます