中学数学「空間図形」の表面積。
さいごは高校入試過去問から難問を2つ出します。
基本・応用とここまで見てきたあなたなら、解けるはず。
難問:高校入試問題から
発展問題でよくみかけるのは
- 複雑な立体の表面積
- 紙コップをころがす問題
という2種類です。
それぞれ宮崎県と滋賀県の高校入試問題から出題します。
あえてくわしい解説はしないので、ぜひチャレンジしてみてください。
組み合わせた立体の表面積
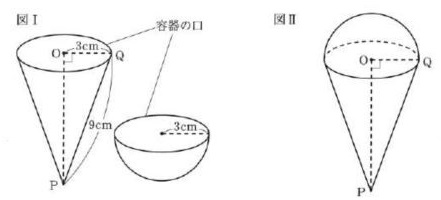
例題9)図Ⅰのような円錐と半球の容器があり、OQ=3cm、PQ=9cm、半球の半径3cmとする。この2つの容器の口をぴったりと重ねて、図Ⅱの立体をつくった。この立体の表面積を求めなさい。
2019 宮崎県公立高校入試問題 5-2
【ヒント】
複雑な図形を解くコツは「分けて、たす」「大きく求めて、ひく」のどっちか。
*複雑な図形については以下の記事内でも解説しています。
…
……。
では、解答です。
【解答例】
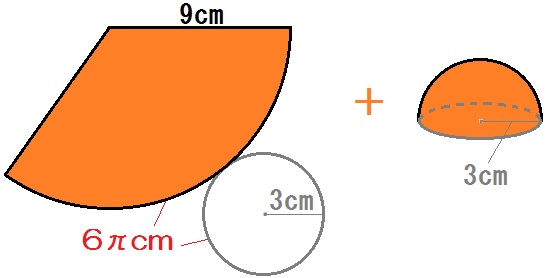
円錐の側面積は、
$$ \mbox{割合}= \frac{6 \pi}{18 \pi} = \frac{1}{3} $$
より
\begin{eqnarray} & &9 \times 9 \times \pi \times \frac{1}{3} \\ &=& 27 \pi \end{eqnarray}
(または 側面積=半径×母線× \(\pi\) より \(3 \times 9 \times \pi = 27 \pi\) )
半球の表面積は、
\begin{eqnarray} & &4 \pi \times 3 \times 3 \times \frac{1}{2} \\&=& 18 \pi \end{eqnarray}
よって求める表面積は、
\begin{eqnarray} & &27 \pi \ + \ 18 \pi \\&=& 45 \pi \end{eqnarray}
答. \(45 \pi\) ㎠
円の面積は含めないことに注意しましょう。
表面積って、表側にある面だけを足すからね。
そこさえ注意すれば、難問ってゆったけど、それほど難しくはないですね。
紙コップをころがす問題
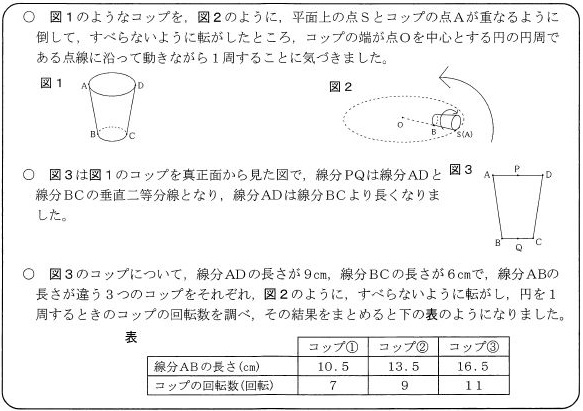
例題10)花子さんは、テーブルの上の紙コップが床に落ちたとき、横に倒れカーブを描きながら転がることに興味をもち、調べたことをまとめました。後の(1)(2)に答えなさい。
(1) 花子さんは、コップ③を図2のように、すべらないように転がしたときの半径OAの長さについて考えました。半径OAの長さを \(r\) cmとして、\(r\) の値を求めなさい。
(2) 花子さんは、下の図4のように、コップを1回転させたときの∠AOSの大きさについて考えました。コップ②を1回転させたときの∠AOSの大きさを求めなさい。
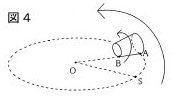
2019 滋賀県公立高校入試問題 3-1,2
【ヒント】
○(紙コップの口の円周)×(コップの回転数)=(大きな円の円周)となる。
○長い文章題が苦手な人は、表や図をかいて整理するといい。
*表や図をかいて整理することについては、以下の記事でも解説しています。
…
……。
では、解答です。
【解答例】
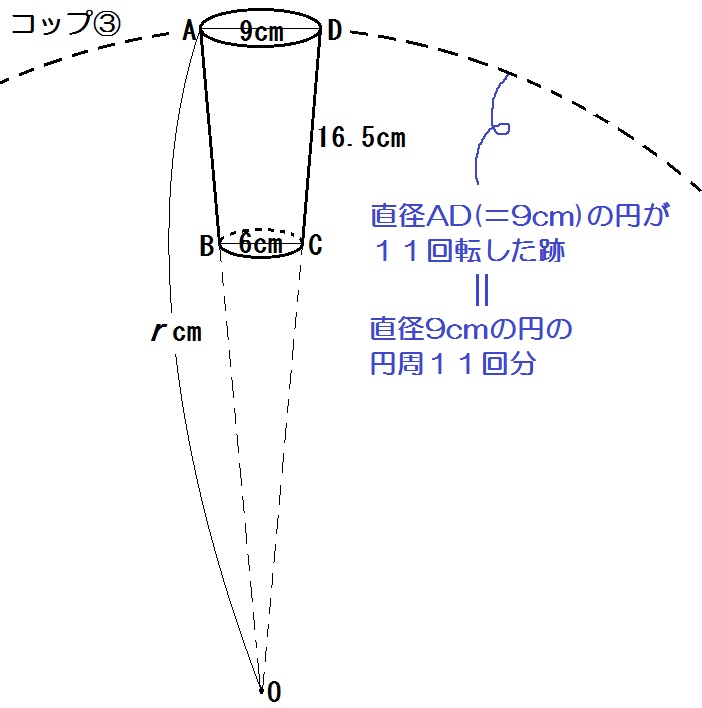
(1) コップ③を転がしたときの円Oの円周は、直径9cmの円が11回転したものなので
$$ 9 \pi \times 11 = 99 \pi \mbox{(cm)} $$
よって、円Oの半径OAの長さを \(r\) cmとすると、
\begin{eqnarray} 2 \pi r &=& 99 \pi \\ r &=& \frac{99}{2} \end{eqnarray}
答. \(r= \frac{99}{2}\) (49.5)
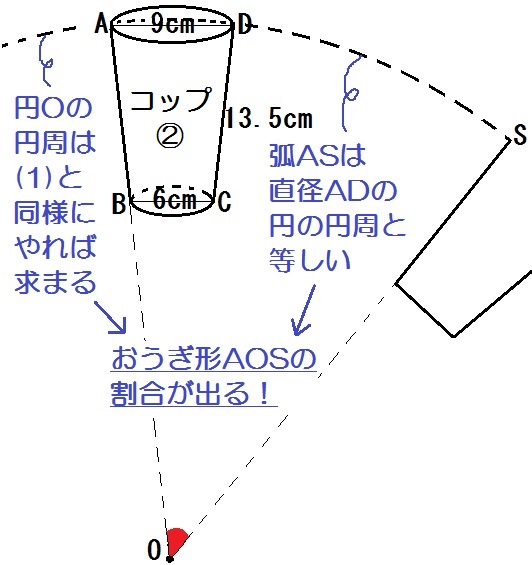
(2) コップ②を転がしたときの円Oの円周は、直径9cmの円が9回転したものなので
$$ 9 \pi \times 9 = 81 \pi \mbox{(cm)} $$
また弧ASの長さは、直径9cmの円の円周と等しいので、\(9 \pi\) cm。
よって、おうぎ形AOSの割合は
$$ \frac{9 \pi}{81 \pi} = \frac{1}{9} $$
したがって
\begin{eqnarray} \mbox{∠AOS} &=& 360 \mbox{°} \times \frac{1}{9} \\ &=& 40 \mbox{°} \end{eqnarray}
答. 40°
最後は表面積とはちょっと違いましたが、この記事の流れから載せてみました。
円とおうぎ形について根っこから理解していれば、このような入試問題も難しくありませんね。
おつかれさまでした。
まとめ

○表面積の求め方の基本は展開図をかくこと。
ただし球の表面積は \(4 \pi r^2\) (心配ある事情)という公式を使う。
○展開図をかけば、
- 円柱:「円周の長さ=長方形の横の長さ」
- 円錐:「円周の長さ=おうぎ形の弧の長さ」
とわかる。
○円錐の表面積の公式として
- 円錐の側面積=(半径)×(母線)× \(\pi\)
- 円錐の表面積=(半径)×(母線+半径)× \(\pi\)
があるが、頼りすぎないこと。
円とおうぎ形の基本をしっかり理解してはじめて、応用や難問に太刀打ちできる。
≪「空間図形」の記事一覧≫
次回は中1空間図形の最後として、立体の切断問題を解説します。
とくに「立体の切り口がどんな図形になるのかイメージできない」という中学生が多いので、攻略法を解説する予定です。




コメント
円錐では、円周と円弧が等しい、という考え方が大切なのはその通りだと思いますが、それを理解した上で、Θ=r1/r2×360゚は使えるようにした方がよいと思います。計算を簡単にするために。
最後のコップを転がす問題も、単純に、9回回転して一周(360゚)するのだから、単純に、360゚×1/9でよいのでは。
なお、最後のコップの問題は、実際には続きがあるんですよね?
上の問題では使わない条件があるので、惑わされる人がいるのではと思いました。
円錐の側面積 半径×母線×π ←これはいい
円錐の表面積 半径×(半径+母線)×π ←混乱します。
単純に
表面積=(側面積)+(底面積)
=(半径×母線×π)+(半径の二乗×π)
で解く方法ではいけないのでしょうか?
混乱するならその方法でもいいと思います。
この記事でジュウゴが言いたかったことは「公式に頼っていては円錐の応用問題が解けない」ということなので、ぶっちゃけ公式などどうでもいいんですが、いちおうの流れで公式っぽく単純な形にして紹介したまででした。