中1数学「平面図形」の円とおうぎ形、つづいて
- おうぎ形の半径の求め方
- 円とおうぎ形の複合図形
という応用問題を解説します。
おうぎ形の半径の求め方
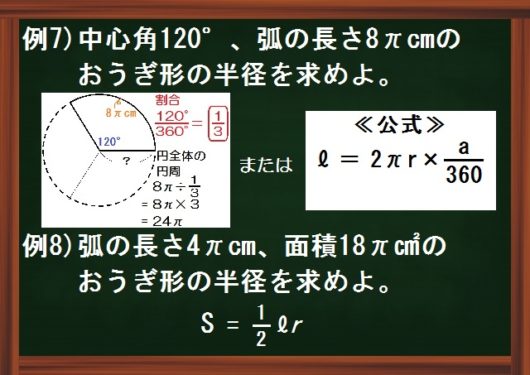
おうぎ形の半径の求め方は、公式を使わないやり方/使うやり方、両方があります。
ここではどちらも紹介します。
公式を使わない求め方
いままでの例題では、
【半径】&【中心角 or 弧 or 面積のどれか1つ】
という2つがわかっていました。
しかしこの例題7では、
【中心角 & 弧】
という2つがわかっていて、逆に半径がわかりません。
こーゆーのが半径を求める問題です。
まず何をしたらいいか?
やっぱり、割合を出します。
$$ \mbox{割合} = \frac{\mbox{おうぎ形}}{\mbox{円全体}} = \frac{\mbox{120°}}{\mbox{360°}} = \frac{1}{3}$$
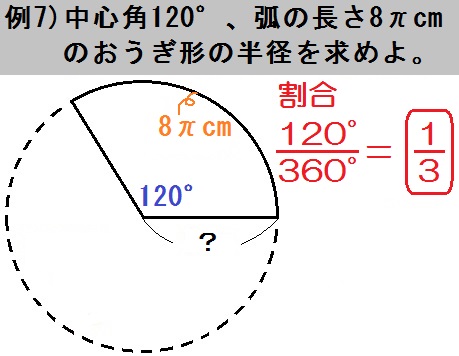
次にするのは、いままでとは逆に、弧の長さから円全体の円周を求めます。
弧 \(8 \pi\) cmというのが円周の \(\frac{1}{3}\) 。
じゃ円周は \(8 \pi\) の3倍すればいいですね。
(いちおう丁寧に言うと、\(\frac{1}{3}\) で割ればいいですね)
$$ \mbox{円周} = 8 \pi \div \frac{1}{3} = 8 \pi \times 3 = 24 \pi $$

あとは、円周が \(24 \pi\) cmになる半径ってなんぼ?と求めるだけ。
暗算で \(12\) cm( \(\pi\) をとって半分)とやってもいいし、半径 \(r\) cmと置くなら
$$ 2 \pi r = 24 \pi $$
という方程式を解いてもいい。
いずれにしろ、答.\(12\) cmと出ます。
以上のように、
- 中心角から割合を出す
- 弧の長さを割合で割って円周を求める
- (半径)×2× \(\pi\) =(円周) を解く
という手順で、公式を使わずにおうぎ形の半径を求めることができます。
[参考記事]
・中1「1次方程式」① 導入
公式を使う求め方
おなじ例題7を、今度は公式を使って解いてみます。
前ページをちゃんと読んだ中学生はもう、
$$ \mbox{弧の長さ} \quad l = 2 \pi r \times \frac{a}{360} $$
$$ \mbox{面積} \qquad S = \pi r^2 \times \frac{a}{360} $$
* \(r\) は半径、 \(a\) は中心角
という公式の意味を理解できてますね。
- 弧の長さ=円周×割合
- 面積=円の面積×割合
だと。
理解できてるなら、あとは上の公式に「中心角120°」「弧の長さ \(8 \pi\) cm」を当てはめるだけです。
\begin{eqnarray} 8 \pi &=& 2 \pi r \times \frac{120}{360} \\ 8 \pi &=& 2 \pi r \times \frac{1}{3} \\ \frac{2}{3} \pi r &=& 8 \pi \\ \frac{2}{3}r &=& 8 \\ r &=& 12 \end{eqnarray}
これが公式を使って半径を求める方法です。
なお、3行目から4行目にかけて両辺を \(\pi\) で割ってますが、\(\pi=3.141592\ldots\) という数字だと理解していれば、納得できるはずです。
[関連記事]
空間図形④ 表面積の問題のコツ
発展問題(\(S=\frac{1}{2}lr\))
ここでついでに発展問題も紹介します。
基本さえわかればいいという人はとばしてかまいません。
この半径を求める問題、中心角がわかりません。
なので、割合を出すことができません。
どーすんの?
以下の公式を使います。
半径 \(r\) 、弧の長さ \(l\) のおうぎ形の面積 \(S\) は
$$ S= \frac{1}{2} lr $$
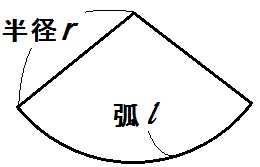
この公式に「弧の長さ \(4 \pi\) cm」「面積 \(18 \pi\) ㎠」を当てはめて、
\begin{eqnarray} 18 \pi &=& \frac{1}{2} \times 4 \pi \times r \\ 18 \pi &=& 2 \pi r \\ 2 \pi r &=& 18 \pi \\ r &=& 9 \end{eqnarray}
答.\(9\) cmと出ます。
なお、この公式 \(S= \frac{1}{2} lr\) は
$$ l = 2 \pi r \times \frac{a}{360} $$
$$ S = \pi r^2 \times \frac{a}{360} $$
という2つを組み合わせて導き出すことができます。
時間のある人はやってみてください。
[参考記事]
・中2数学「等式の変形」
練習問題
以上、おうぎ形の半径の求め方でした。
公式を使うか使わないか、それはあなた次第です。
ミスが少なく、速くできるほうでやりましょう。
それでは、練習問題を用意しましたのでどうぞ。
解答は末尾に記載、質問はコメント欄から。
問6)中心角72°、弧の長さ \(6 \pi\) cmのおうぎ形の半径を求めよ。
問7)中心角80°、弧の長さ \(10 \pi\) cmのおうぎ形の半径を求めよ。
問8)弧の長さ \(6 \pi\) cm、面積 \(12 \pi\) ㎠のおうぎ形の半径を求めよ。
6:15cm 7:\(\frac{45}{2}\) cm(22.5cm) 8:4cm
>Amazonプライム・ビデオ「きっと、うまくいく(字幕版)」
円とおうぎ形の複合図形

最後に円とおうぎ形の複合図形、つまり円とおうぎ形が組み合わさって色のついた問題の解き方です。
コツは
- 分けて、たす
- 大きく求めて、ひく
という2パターンを使いこなすことです。
色のついた周囲の長さ
このような周囲の長さを求める問題では、「分けて、たす」こと。
つまり、おうぎ形の弧など、あなたが求め方を知ってる部分に分けて、それらを足せばいい。
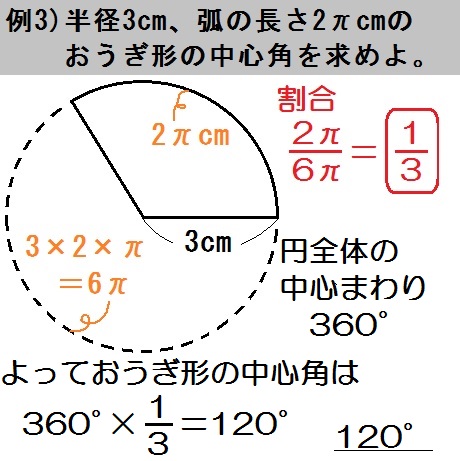
ようするに、こーゆーことです↓
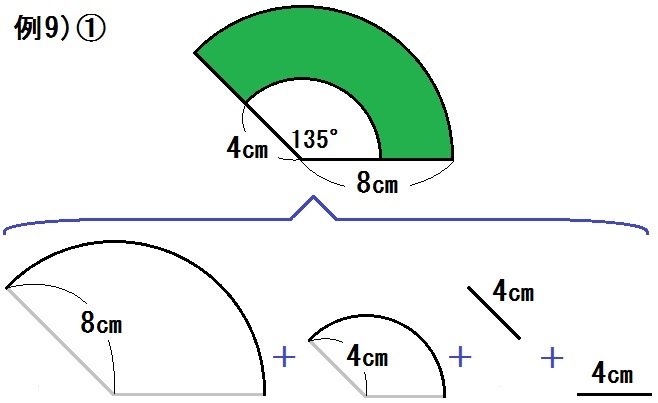
*おうぎ形の割合はどちらも \(\frac{135}{360} = \frac{3}{8}\) なので
\begin{eqnarray} & &8 \times 2 \times \pi \times \frac{3}{8} + 4 \times 2 \times \pi \times \frac{3}{8} + 4 + 4 \\ &=& 6 \pi + 3 \pi +4 +4 \\ &=& 9 \pi +8 \end{eqnarray}
答.\(9 \pi +8\) (cm)

*おうぎ形の割合はどちらも \(\frac{1}{4}\) なので
\begin{eqnarray} & &4 \times 2 \times \pi \times \frac{1}{4} + 4 \times 2 \times \pi \times \frac{1}{4} + 4 + 4 \\ &=& 2 \pi + 2 \pi +4 +4 \\ &=& 4 \pi +8 \end{eqnarray}
答.\(4 \pi +8\) (cm)
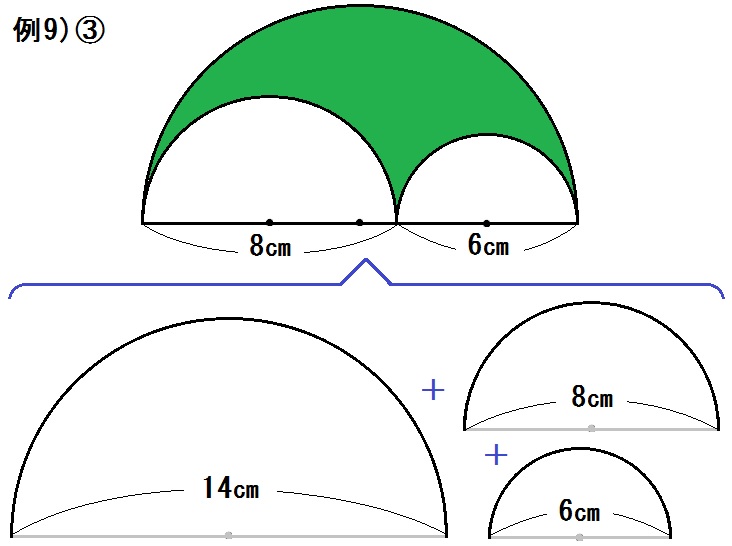
*おうぎ形の割合はぜんぶ \(\frac{1}{2}\) なので
\begin{eqnarray} & &14 \pi \times \frac{1}{2} + 8 \pi \times \frac{1}{2} + 6 \pi \times \frac{1}{2} \\ &=& 7 \pi + 4 \pi + 3 \pi \\ &=& 14 \pi \end{eqnarray}
答.\(14 \pi\) cm
①や②の問題では、直線部分も足すってこと、忘れやすい。
注意しよう!
色のついた面積
このような面積を求める問題では、「分けて、たす」と「大きく求めて、ひく」を組み合わせること。
つまり……見たほうが早いね。
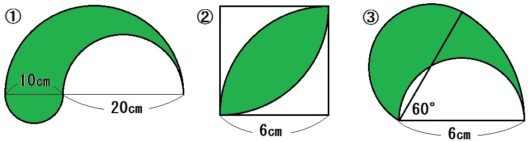
ようするにこーゆーこと↓
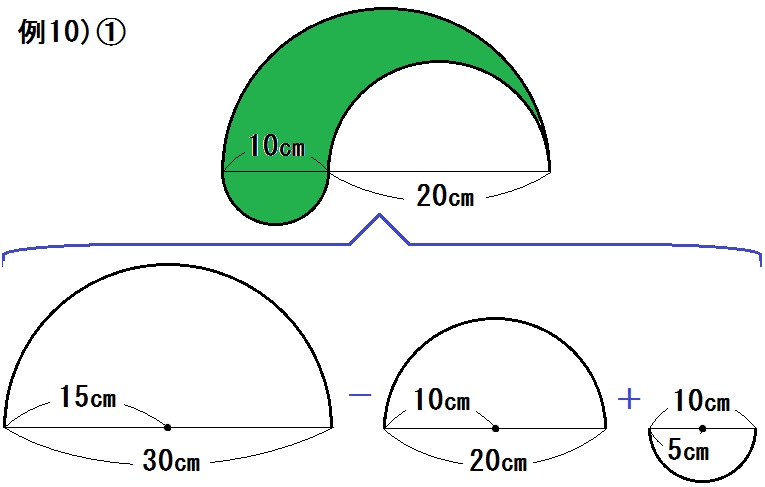
*おうぎ形の割合はぜんぶ \(\frac{1}{2}\) なので
\begin{eqnarray} & &15 \times 15 \times \pi \times \frac{1}{2} – 10 \times 10 \times \pi \times \frac{1}{2} + 5 \times 5 \times \pi \times \frac{1}{2} \\ &=& \frac{1}{2} \pi (225-100+25) \\&=& \frac{1}{2} \pi \times 150 \\&=& 75 \pi \end{eqnarray}
答.\(75 \pi \) ㎠
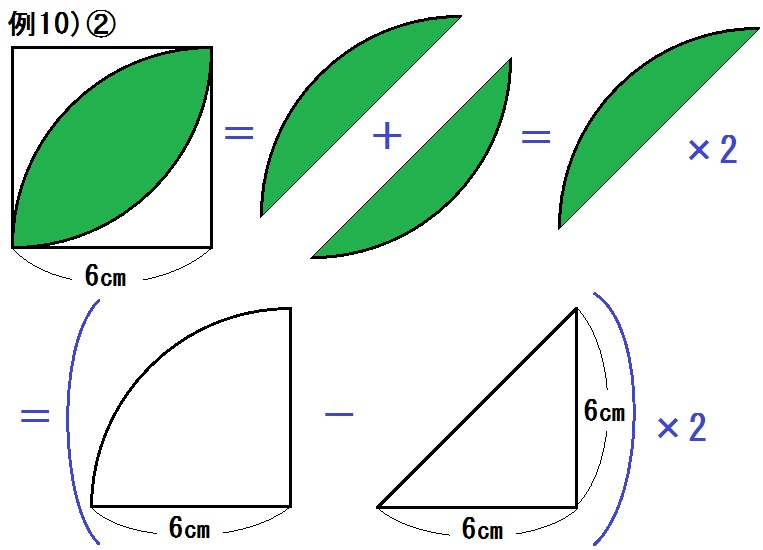
*おうぎ形の割合は \(\frac{1}{4}\) なので
\begin{eqnarray} & & \left( 6 \times 6 \times \pi \times \frac{1}{4} – 6 \times 6 \times \frac{1}{2} \right) \times 2 \\&=& (9 \pi -18) \times 2 \\&=& 18 \pi -36 \end{eqnarray}
答.\(18 \pi -36\) (㎠)
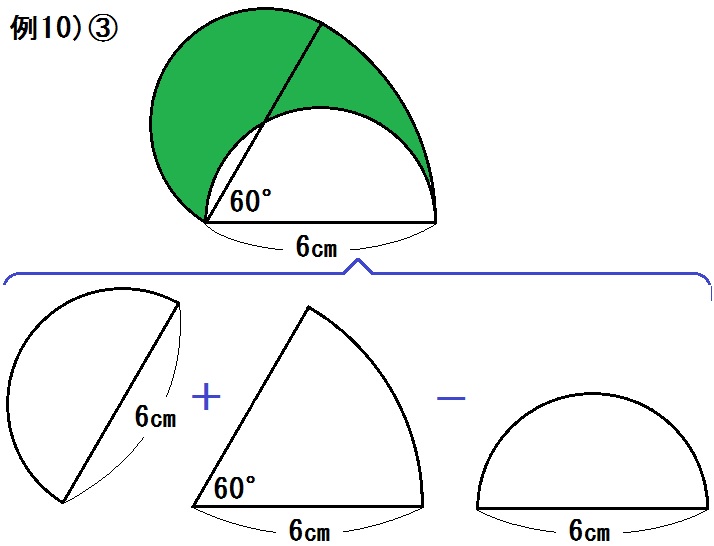
*半円どうしは打ち消しあう
*2番目のおうぎ形の割合は \(\frac{60}{360}= \frac{1}{6}\) なので
\begin{eqnarray} & & 6 \times 6\times \pi \times \frac{1}{6} \\&=& 6 \pi \end{eqnarray}
答.\(6 \pi \) ㎠
周じゃなくて面積なんで、
(半径)×(半径)× \(\pi\)
ってことに注意しよう。
複合図形問題が「できる」ために大切なこと
以上が、複合図形問題の解き方です。
コツは
- 分けて、たす
- 大きく求めて、ひく
の2つ。
解き方は「わかった」でしょう。
しかし自分でいざ解いてみて「できた」となるためには、ほかに3点ほど大切なことがあります。
1つ。
じっさいに分けた図を描いてみること。
「どう分けていいかわからない」という中学生ほど、自分で図を描くことを怠っています。
はじめはわからなくて当たり前。
でも自分で「ああかな、こうかな」とたくさん描くうちに、自然と分け方が身につきます。
複合図形問題では必ず余白に分けた図を描きましょう。

2つ。
式はつなげて書いたほうが、計算が速い。
たとえば、例題10①の式を、3つに分けて書いちゃうとこんな感じ↓
\begin{eqnarray} & &15 \times 15 \times \pi \times \frac{1}{2} = \frac{225}{2} \pi \\& & 10 \times 10 \times \pi \times \frac{1}{2} = 50 \pi \\& & 5 \times 5 \times \pi \times \frac{1}{2} = \frac{25}{2} \pi \end{eqnarray}
$$ \frac{225}{2} \pi -50 \pi + \frac{25}{2} \pi = 75 \pi $$
これでもいいんです。
ただ、上に書いた解答例では、つなげて書くことで \(\frac{1}{2} \pi\) でくくれるから、計算がラクになってますよね。
だから、式はつなげて書くほうをおすすめします。
これは中1よりもむしろ、中3以上へのアドバイス。
なぜなら受験と高校数学では計算スピードが大切になるから。

3つ。
複合図形問題は、公式丸暗記のままでは解けない。
たとえば例題9③を、
「\( 2 \pi r \times \frac{a}{360}\) に当てはめて、半径は14cmの半分の7cmで、それから中心角は180°で…」とやるか。
それとも
「ん?円周の半分やん、\(14 \pi \times \frac{1}{2}\) …」とできるか。
おうぎ形をちゃんと理解しているかどうかが、この複合図形問題で試されるんです。
だからこそ、前ページであれだけ詳しく解説しました。
まだ公式丸暗記の中学生は、まずおうぎ形の基本をしっかり理解しましょう。
練習問題
それでは、以上3点と
- 分けて、たす
- 大きく求めて、ひく
というコツを意識しながら、最後の練習問題をどうぞ。
解答は末尾に記載、質問はコメント欄から。
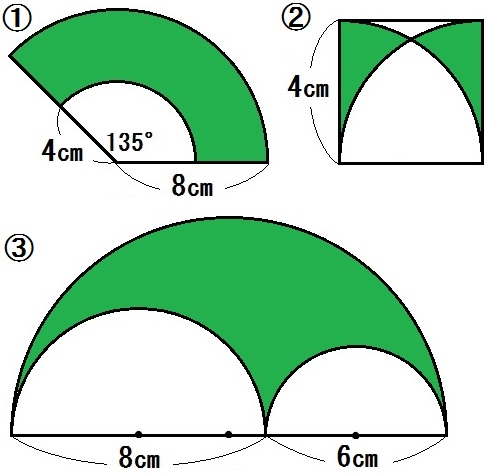
問9)下の図で、色をつけた部分の周囲の長さと面積を求めよ。
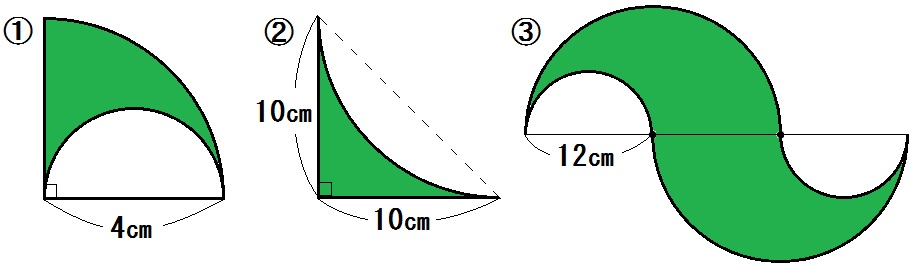
①周 \(4 \pi +4\) (cm) 面積 \(2 \pi\) ㎠
②周 \(5 \pi +20\) (cm) 面積 \(100- 25 \pi\) (㎠)
③周 \(36 \pi\) cm 面積 \(108 \pi\) ㎠
>Amazonプライム・ビデオ「リリィ、はちみつ色の秘密 (字幕版)」
まとめ

【おうぎ形の基本】
- 「\(\pi\)」とは円周率3.141592…という数字を表す定数
- おうぎ形とは円の一部
【中心角・弧・面積の求め方】
- 中心角・弧・面積のうち、わかっている1つから \(\frac{\mbox{おうぎ形}}{\mbox{円全体}}\) という割合を出す
- 円全体を求める
- (円全体)×(割合)をする
*公式は覚えなくていい!
【おうぎ形の半径の求め方】
- 中心角から割合を出す
- 弧の長さを割合で割って円周を求める
- (半径)×2× \(\pi\) =(円周) を解く
または
$$ \mbox{弧の長さ} \quad l = 2 \pi r \times \frac{a}{360} $$
という公式に当てはめる。
*発展問題 \(S= \frac{1}{2} lr\)
【円とおうぎ形の複合図形】
コツは
- 分けて、たす
- 大きく求めて、ひく
そして「できる」ようになるためには
- じっさいに分けた図を描いてみる
- 式はつなげて書いたほうが計算が速い
- 公式丸暗記のままでは解けない
おつかれさまでした。
以上で中1数学「平面図形」が終了です。
次回からは中1数学「空間図形」単元を解説していきます。
[中学数学「平面図形」の記事一覧]





コメント
問9の3の周りの長さの解説お願いします。
直径24cmの円周ひとつぶん+直径12cmの円周ひとつぶん
式をつなげて書く、というのは、地味に大事だと思います。
理由としては、上に挙げられている、計算が楽、のほか、
個々に計算した後、足したり引いたりすると、
足すのを忘れたり、引くのを忘れたり、ということが往々にしてあるので、
最初につなげて書くことで、それを防げる、ということも言えるかと思います。