つづいて、円錐の表面積の求め方を解説します。
ポイントとなるコツはひとつだけ。
このコツをしっかりマスターすれば、円錐の表面積問題はバッチリです。
応用:円錐の表面積
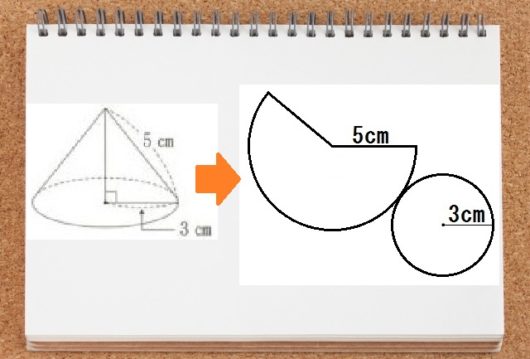
円錐の展開図は上図のように、円ひとつ・おうぎ形ひとつになります。
ここで、展開するまえにどこが接していたか考えれば、
円周の長さ=おうぎ形の弧の長さ
ということがわかる。
円錐の表面積のポイントはこれだけです。
円錐の表面積の求め方
側面積とは側面の面積のこと、表面積とは側面積もあわせてぜんぶの面積。
つまり円錐の場合、展開図において
- 側面積=おうぎ形の面積
- 表面積=おうぎ形の面積+円の面積
ということです。
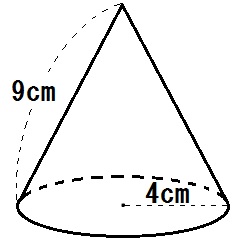
ちなみに例題4の図の9cm部分を「母線」といいます。
さて、表面積の求め方の基本にそって展開図をかきます↓
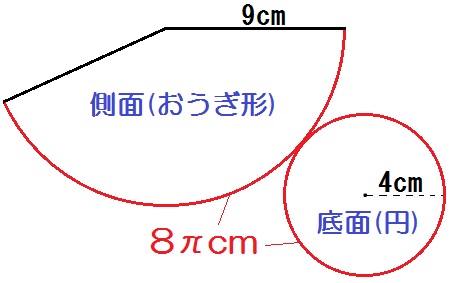
展開図をかいたら、さっそくコツを使う。
円周の長さ=おうぎ形の弧の長さで、円の半径4cmがわかってる。
よって円周の長さもおうぎ形の弧の長さも、\(8 \pi\) cmとわかる。(←円周=直径× \(\pi\))
こうして共通部分の長さを出したら、あとは側面積つまりおうぎ形の面積を求めるだけです。
おうぎ形については平面図形⑤ 円とおうぎ形でくわしく解説しましたね。
おうぎ形って円の一部だから、割合を出せばいいんだと。
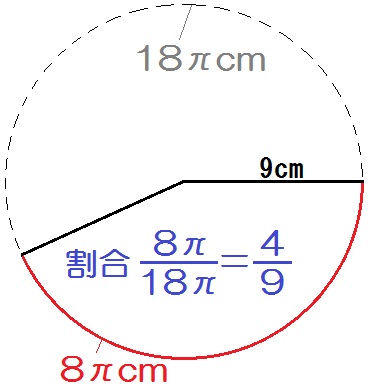
全体の周が \(18 \pi\) cmなので、割合は
$$ \frac{8 \pi}{18 \pi} = \frac{4}{9} $$
と出ます。
よって、おうぎ形の面積は
\begin{eqnarray} & & 9 \times 9 \times \pi \times \frac{4}{9} \\ &=& 36 \pi \end{eqnarray}
側面積. \(36 \pi\) ㎠と出ます。
また円錐ぜんぶの表面積は、これに円の面積を足せばいいから
\begin{eqnarray} & & 36 \pi \ + \ 4 \times 4 \times \pi \\&=& 36 \pi \ + \ 16 \pi \\&=& 52 \pi \end{eqnarray}
表面積. \(52 \pi\) ㎠と出ます。
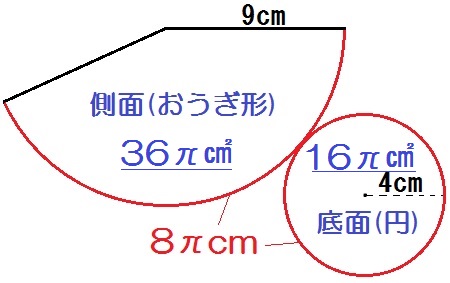
このように、円錐の表面積のポイントは円周の長さ=おうぎ形の弧の長さだけ。
もし以上の解説がよくわからないのであれば、それは表面積の単元でなく、平面図形:円とおうぎ形単元でつまずいています。
というか、そういう中学生がほとんど。
とくにおうぎ形の問題を公式に頼ってやってきたという人ほど、ここでつまずきます。
だからこそ、円とおうぎ形の記事は3ページにわたってくわしく解説しました。
この解説が腑に落ちないという人はいますぐ下の記事から復習してください。
また指導者や講師の方も、おうぎ形を根本から理解させたうえで円錐の表面積に入るという流れを、ぜひ参考にしてください。
円錐の表面積の公式
ここでちょっと、半径と母線を文字で一般化して、円錐の側面積・表面積を求めてみます。
やり方は例題5とまったく同じです。
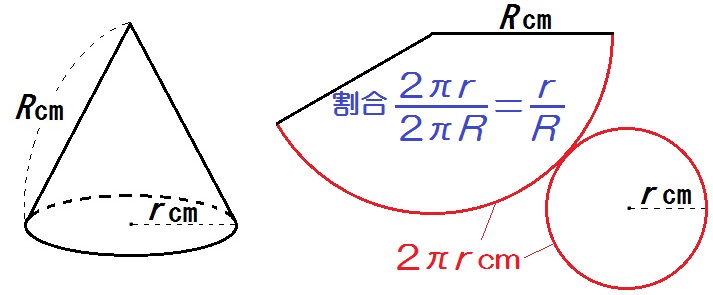
まず円周の長さ=おうぎ形の弧の長さ= \(2 \pi r\) cm。
よっておうぎ形の割合は
$$ \frac{2 \pi r}{2 \pi R} = \frac{r}{R} $$
したがって、おうぎ形の面積つまり側面積は
\begin{eqnarray} & & R \times R \times \pi \times \frac{r}{R} \\ &=& \pi rR \end{eqnarray}
また、表面積は
\begin{eqnarray} & & \pi rR \ + \ r \times r \times \pi \\&=& \pi rR \ + \ \pi r^2 \\&=& \pi r(R+r) \end{eqnarray}
こうして、円錐の側面積・表面積の公式が出てきました。
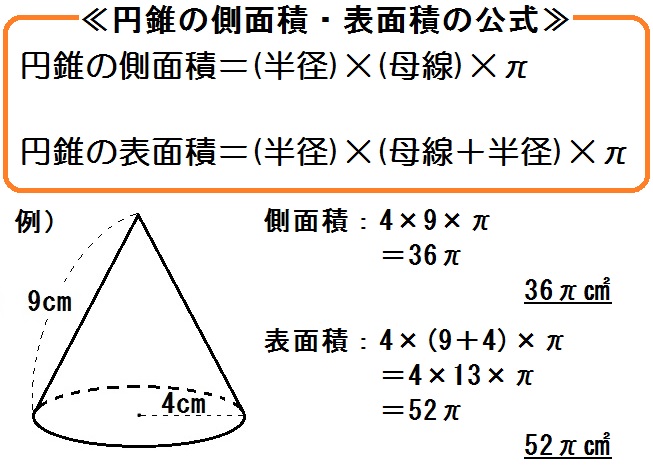
円錐の半径と母線がともにわかってる場合、この公式を使うとイッパツで側面積・表面積が出ます。
時間短縮につながるので、おぼえておいて損はないでしょう。
ただ、公式だけを丸暗記するのはやめてください。
なぜなら次の例題7、例題8のような高校入試問題が解けなくなるからです。
おうぎ形の中心角を求める
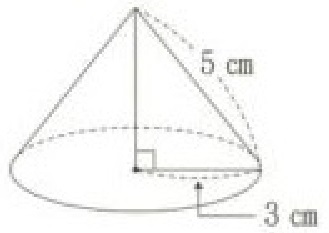
例題7)下の図のように、半径が3cmの円を底面とし、母線の長さが5cmとなる円錐があります。また、この円錐の展開図で、側面になるおうぎ形をPとします。おうぎ形Pの中心角を求めなさい。
2019 宮城県公立高校入試問題 2-4-1
例題7で求めるのは、側面積や表面積じゃなく、おうぎ形の中心角。
ただ「この円錐の展開図で」と言ってるので、なにはともあれ展開図をかきましょう。
かいたら、求める中心角がどこかわかりますね↓
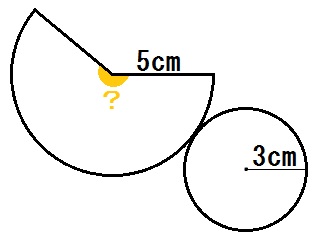
さて、円とおうぎ形の記事でやりましたが、中心角・弧・面積を求めるには、3つのどれか1つから割合を出せばよかった。
ここで円錐の表面積のコツ:「円周の長さ=おうぎ形の弧の長さ」を使えばいい。
いま、底面の半径3cmのほうがわかってるんで、円周の長さもおうぎ形の弧の長さも \(6 \pi\) cmとわかる。(←円周=直径× \(\pi\))
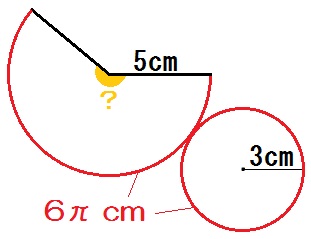
また全体の周は \(10 \pi\) cmなので、おうぎ形の割合は
$$ \frac{6 \pi}{10 \pi} = \frac{3}{5} $$
と出ます。
よって、おうぎ形の中心角は
$$ 360 \mbox{°} \times \frac{3}{5} = 216 \mbox{°} $$
中心角. 216°
このように、おうぎ形の中心角を求める問題であっても、例題5とやり方は同様です。
「おうぎ形って円の一部だから、割合を求めたらいい」という平面図形でやったコツに、「円錐の展開図では、底面の円周の長さ=おうぎ形の弧の長さ」という空間図形のコツを合わせるだけ。
これがわかれば、側面積だろうが中心角だろうが解いていけます。
底面の円の半径を求める
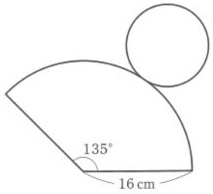
例題8)下の図は、円錐の展開図である。この展開図を組み立てたとき、側面となるおうぎ形は、半径が16cm、中心角が135°である。底面となる円の半径を求めなさい。
2019 徳島県公立高校入試問題 1-8
もう1問、円錐の高校入試問題をやってみましょう。
例題8は展開図をかいてくれています。
そして今回は例題7と逆に、おうぎ形の中心角が与えられていて、求めるものが底面の円の半径です。
…もうわかりますね?
例題7と逆の順序でやればいいと。
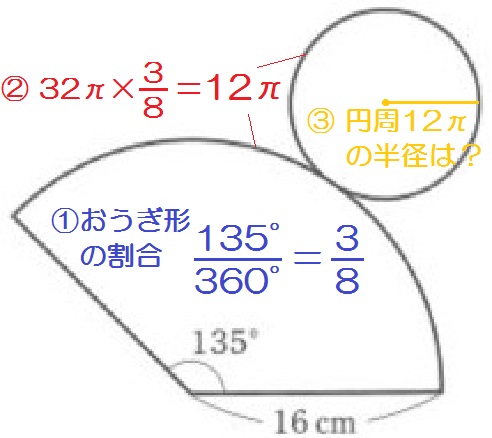
解答例)
おうぎ形の中心角135°より、おうぎ形の割合は
$$ \frac{135 \mbox{°}}{360 \mbox{°}} = \frac{3}{8} $$
よっておうぎ形の弧の長さは
$$ 32 \pi \times \frac{3}{8} = 12 \pi $$
つまり底面の円の円周も \(12 \pi\) cm。
ここで底面の円の半径を \(r\) cmとすると、
\begin{eqnarray} 2 \pi r &=& 12 \pi \\ r &=& 6 \end{eqnarray}
答. 6cm
もちろん解答の終盤は「\(12 \pi\) から \(\pi\) をとって半分にして、\(6\)」と暗算してもOKです。
ただこういう方程式をつくって解くという大切さも、前回の「円柱の高さを求める問題」で解説しましたね。中学生は徐々に慣れていってください。
以上、円錐の表面積にかんする問題を4つ紹介しました。
冒頭で述べたとおり、コツは円周の長さ=おうぎ形の弧の長さというひとつだけ。
「それでもできない」という中学生は、円とおうぎ形の基本をちゃんと身につけることです。
では最後に、表面積問題の難問を2つ、高校入試過去問から紹介します。




コメント
円錐では、円周と円弧が等しい、という考え方が大切なのはその通りだと思いますが、それを理解した上で、Θ=r1/r2×360゚は使えるようにした方がよいと思います。計算を簡単にするために。
最後のコップを転がす問題も、単純に、9回回転して一周(360゚)するのだから、単純に、360゚×1/9でよいのでは。
なお、最後のコップの問題は、実際には続きがあるんですよね?
上の問題では使わない条件があるので、惑わされる人がいるのではと思いました。
円錐の側面積 半径×母線×π ←これはいい
円錐の表面積 半径×(半径+母線)×π ←混乱します。
単純に
表面積=(側面積)+(底面積)
=(半径×母線×π)+(半径の二乗×π)
で解く方法ではいけないのでしょうか?
混乱するならその方法でもいいと思います。
この記事でジュウゴが言いたかったことは「公式に頼っていては円錐の応用問題が解けない」ということなので、ぶっちゃけ公式などどうでもいいんですが、いちおうの流れで公式っぽく単純な形にして紹介したまででした。