中学数学のつまずき解消をめざすこの連載。
今回からいよいよ「1次方程式の利用」、つまり文章題に入ります。
方程式の文章問題を解く手順は以下のとおりです。
(1)求めるものを \(x\) とする
(2)等しい関係をみつけて方程式をつくる
(3)方程式を解く
(4)問題に合っているか確かめる
この手順はすでにいろんな所で言われているので、知っているという人もいるでしょう。
でも、自分で実際に解こうとするとできない。
これがつまずく本当の原因ですよね。
とくに(1)と(2)の段階で困ることが多い。
「求めるものが2つあるときはどうすればいいの?」
「等しい関係って、どうみつけたらいいの?」
こんな悩みを抱える中学生を、わたしは数千人以上も指導してきました。

そこでここからは、問題パターン別に、文章問題の解き方のコツをぜんぶ伝授します。
つまり、「こんな問題ならこっちを x とする」とか、「こういう場合はこうやって式をつくる」というパターンを、ぜんぶ紹介します。
代金や個数、分配、年齢、整数や自然数、平均、過不足の問題、道のりの問題、割合の問題、図形の問題、規則性の問題…
ぜんぶのパターンが頭に入ったら、どんな問題でもやっつけられます。
だからひとつずつ焦らず、解き方のコツを身につけていってください。
1回目は「代金と個数」。
ここで方程式文章題の基本となる考え方も合わせて紹介します。
今後のすべての問題の基礎となるので、かならず読んでから次に進んでくださいね。
[関連記事]
○文章題①【代金、個数】
方程式文章題の基本の解き方

それでは、以下の例題を解いていきながら、文章題の基本を学びましょう。
方程式の手順に沿って、ていねいにやっていきます。
これくらいわかる!って人も、最初なんでまぁ付きあってください。
スポンサーリンク
(1)求めるものを \(x\) とする
まず求めるものは「みかんの個数」です。
よって一行目には「みかんの個数を \(x\) 個とする」等と書きます。

このとき、\(x\) に単位があればかならず付けること。
「みかんの個数を \(x\) とする」等と書いちゃう中学生、注意です。
なぜなら最初に単位を書かないと、\(x\) が何を表しているんだったか、あやふやになるから。
いまはまだいいですが、過不足・速さ・図形の問題などで困ります。
「長いす13人」と答えてしまったり。
道のりを \(x\) としたのに、時間とごっちゃにしたり。
面積を求めるのに「45cm」で終わったり。
こういうミスのないよう、\(x\) に単位があれば必ず付けましょう。
(2)等しい関係をみつけて方程式をつくる
次に等しい関係をみつけて、=でつないだ式、つまり方程式をつくります。
これを苦手とする中学生がとても多い。
つまり、文章から式になおすということがむずかしいんですね。
そこで、式をつくるときのコツを3つ伝授します。
「代金と個数」に限らず、あらゆる方程式文章題で役立つコツです。
それは↓
①イラストを描いてイメージする
②x の代わりに具体的な数字を入れてみる
③何算するか考える
①まず文章問題は「何を言ってるのかイメージしにくい」というのが難点です。
文章だけですからね。マンガじゃないし、イラスト付きでもないし。
だから自分で、かんたんなイラストを描いてやるんです。
たとえば、こんなかんじ↓
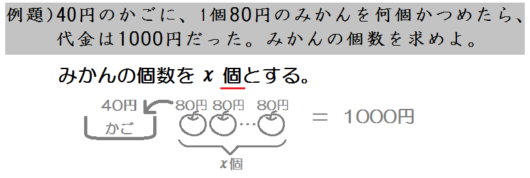
べつに上手な絵じゃなくてかまいません。
自分にとってイメージしやすい、さっと描けるものでいいです。
文章だけじゃイメージしにくい!と感じたら、絵を描く練習と思って、イラストを描くようにしてみてください。
②イラストを描いても、まだどんな式をつくったらいいかわからない。
そんな場合は、\(x\) の代わりに具体的な数字を入れてみます。
たとえばみかんの個数が \(x\) 個じゃなくて \(5\) 個だったら?
1個80円のみかんが \(5\) 個あったら?
みかんの値段は、ぜんぶで、そう、400円ですね。
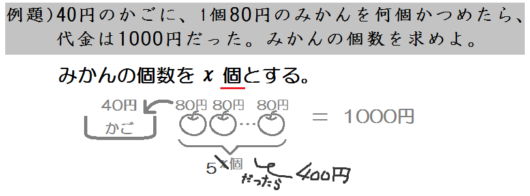
ちなみにこれをかごにつめたら、440円ですね。
③いま、400円は何算で出しましたか?
そう、かけ算。\(80 \times5\) 。
じゃ、\(5\) 個を \(x\) 個に戻したら、みかんの値段はぜんぶで \(80x\) 円。
これを40円のかごにつめます。
440円は何算で出しましたか?
そう、たし算。\(400+40\) 。
だから買った金額の合計は、\(80x+40\) となる。
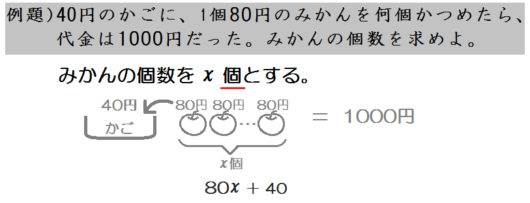
これが1000円と等しいから、方程式は
$$80x+40=1000$$
このように、方程式をつくるときには
①イラストを描いてイメージする
②x の代わりに具体的な数字を入れてみる
③何算するか考える
この3つのコツを常に意識するといいでしょう。
(ちなみにこれらのコツは「文字と式」数量の表し方でも紹介したものです)

(3)方程式を解く
あとは、つくった方程式を解くだけです。
\begin{eqnarray} 80x+40 &=&1000 \\ 80x &=&1000-40 \\ 80x &=&960 \\ x &=&12 \end{eqnarray}
ちなみにこの方程式を解く段階でつまずくという生徒は、文章題ではなく計算に原因があります。
よって、以下の過去記事を参照して、適宜復習してください。
(4)問題に合っているか確かめる
方程式が解けたら、答えの確かめをおこないます。
やりかたは、一行目の文に解を入れてみるんです。

「みかんの個数を \(12\) 個とする」。
おかしい?おかしくない?
おかしくないよね。
これがたとえば
「みかんの個数を \(-12\) 個とする」とか
「みかんの個数を \( \frac{7}{3}\) 個とする」
だったら明らかにおかしい。
計算ミスか、あるいは作った式がまちがってます。
この確かめを、文章題では必ずおこなうこと。
それだけで、正答率がかなりちがってきます。
5秒で終わります。
必ず実施してください。
最後に、単位つきで答えを書きます。

単位忘れや単位まちがいにも注意しましょう。
最後だからって気がぬけて、「12」や「12円」とか書く生徒もいます。
できた解答をながめて、まちがってないかもう一度確認するとよりいいですね。
以上、方程式文章題の基本の解き方でした。

[関連記事]
連立方程式の文章題① 立式のコツ
「代金と個数」問題のコツ(未知数が2つ)

ここまでの話は、どの文章問題にも当てはまる基本です。
ここからは「代金と個数」問題の解き方のコツをお話ししていきます。
[その他の文章問題はこちらから↓]
まず、わからない数が2つある問題。
問題パターン別に例題を出していくので、一緒に考えていきましょう。
合わせて~
例題2)50円のハガキと80円の切手を合わせて10枚買い、620円払った。ハガキと切手をそれぞれ何枚買ったか求めよ。
この例題では、ハガキの枚数と切手の枚数という2つを求めなければなりません。
このように、求めるものが2つある問題のコツは、一方を x とし、もう一方は x を使った式で表すです。
なかでも「合わせて●」という文ならば、好きな方を x とし、もう一方は ●-x と表すことができます。
たとえば例題2の場合、まずハガキの枚数か切手の枚数、好きなほうを \(x\) とします。
好みの問題なんで、どっちでもかまいません。

このようにハガキの枚数のほうを \(x\) とした、とします。
すると、もう一方の切手の枚数は \(10-x\) となります。
(たとえばハガキの枚数が3枚だったら切手は何枚ですか?そう、7枚ですね。いま7を何算で出しましたか?そう、\(10-3\) というひき算ですね。だからハガキが \(x\) 枚なら切手は \(10-x\) 枚となるんです)。

こうして求めるものが両方とも \(x\) を使って表せたら、次は等しい関係をみつけて方程式をつくります。
先に述べた3つのコツも随時活用してくださいね。

あとは方程式を解いて、確かめをして(ついでに切手の枚数も \(10-6=4\) と計算して)、答えを書きます。

このように、「合わせて●」なら、一方を \(x\) とし、他方を●\(-x\) と表す。
これが未知数2つ問題の解き方のコツです。
このコツを利用して、以下の類題も解いてみてください。
(解答は末尾に記載、質問はコメント欄からどうぞ)
問1)1本150円のジュースと1本130円のお茶を合わせて12本買ったら、代金が1720円だった。ジュースとお茶をそれぞれ何本買ったか求めよ。
問2)1個110円のりんごと1個60円のみかんを合わせて8個買って、120円のかごにつめたら、ちょうど700円だった。りんごとみかんをそれぞれ何個買ったか求めよ。
問3)1冊1300円の問題集と1冊100円のノートを合わせて7冊買い、5000円出したら700円のおつりがあった。問題集とノートをそれぞれ何冊買ったか求めよ。
問1)ジュース8本、お茶4本
問2)りんご2個、みかん6個
問3)問題集3冊、ノート4冊
BはAより~
例題3)鉛筆を5本とボールペンを3本買ったら代金が760円だった。ボールペン1本の値段は鉛筆1本の値段より40円高い。鉛筆とボールペンの値段をそれぞれ求めよ。
このような大小問題も、代金と個数でよく出てきます。
つまりAとBという2つの未知数があって、「BはAより~円高い(安い)」とか「BはAより~個多い(少ない)」とか「BはAの~倍」とか「BはAの半分」とかという大小の条件がある問題です。
ここでもわからない数が2つあるので、一方を \(x\) とし、もう一方を \(x\) を使った式で表すというのは同じです。
そして「BはAより~」という条件文がある問題では、Aを x とし、Bを条件文どおりの式で表すというのがコツになります。
たとえば例題3の場合、「ボールペン1本の値段は鉛筆1本の値段より40円高い」とある。
だから鉛筆1本の値段のほうを \(x\) とします。
そしてボールペン1本の値段は、条件文より、\(x+40\) と表せるのです。
(もし鉛筆が100円だったらボールペンは何円?そう、140円ですね。140は何算しましたか?そう、\(100+40\) というたし算ですね。だから鉛筆が \(x\) 円だったらボールペンは \(x+40\) 円なんです)。

こうして未知数2つを表せたら、あとはやることは一緒です。
等しい関係をみつけて方程式をつくる、その方程式を解く、確かめをする(ついでにボールペンの値段も \(80+40=120\) と求める)、最後は単位を忘れずに答えを書きます。

くりかえしますが、未知数が2つあって、かつ「BはAより~」という大小関係の文を見つけたら、Aを \(x\) とする、そしてBは条件どおりに式を作って表すというのがコツです。
たとえば「女子は男子より3人多い」とあれば、男子を \(x\)人とし、女子を \(x+3\)人とする。
「りんごはみかんより4個少ない」とあれば、みかんを \(x\)個とし、りんごを \(x-4\)個とする。
「ニンジンの本数は大根の5倍」とあれば、大根を \(x\)本とし、ニンジンを \(5x\)本とする。
「消しゴムの値段はシャーペンの半分」とあれば、シャーペンを \(x\)円とし、消しゴムを \(\frac{1}{2}x\)円とする。
この解き方のコツを利用して、類似の問題をやっつけていってください。
以下、練習問題を載せておきます。
(答は末尾に記載、質問はコメント欄からどうぞ)
問4)プリン4個とゼリー2個を買ったら代金は780円だった。ゼリーはプリンより30円安い。プリンとゼリーの値段をそれぞれ求めよ。
問5)姉と妹の所持金は合計で5200円で、姉は妹の3倍のお金をもっている。姉と妹の所持金はそれぞれ何円か求めよ。
問6)4mのロープをA,B2人で分ける。BのほうをAより30cm短くするように分けると、A,Bのロープはそれぞれ何cmになるか求めよ。
問4)プリン140円、ゼリー110円
問5)姉3900円、妹1300円
問6)A215㎝、B185㎝
*問6)はいわゆる「分配」問題ですが、未知数2つで大小関係の条件文があるので、ここで紹介した解き方で解けます。
分配問題について詳しくは次回の記事を参照。
「代金と個数」問題のコツ(残金)

最後に「残金」問題の解き方について解説します。
このような残金の問題は求めるものが1つなので、何を \(x\) とするかは難しくありません。
難しいのはそのあと、等しい関係をみつけて方程式をつくるときですね。
ここでのコツは、2段階に分けて考えることです。
つまり、
①それぞれの残金を \(x\) を使って表す
②文に沿って等式(=方程式)をつくる
以下、具体的な解き方を見てみましょう。
例題4)兄は860円、弟は940円持っていたが、同じボールを兄は2個、弟は3個買ったので、兄の残金は弟の残金の3倍になった。ボール1個の値段を求めよ。
まず求めるものは「ボール1個の値段」なので、それを \(x\) とします。

ここから2段階に分けて、方程式をつくっていきます。
①それぞれの残金を \(x\) を使って表す
兄は860円持っていて、\(x\) 円のボールを2個買いました。
兄の残金はいくらですか?
そう、\(860-2x\) ですね。
また弟は940円持っていて、\(x\) 円のボールを3個買いました。
弟の残金はいくらですか?
そう、\(940-3x\) ですね。
このように、まずはそれぞれの残金を \(x\) を使って表しましょう。
(難しい場合はイラストを描く、\(x\) の代わりに具体的な数を入れる、何算するか考えるというコツを使って表してください)。

②文に沿って等式をつくる
残金の問題の場合、文章中にかならず等しい関係を表す一文があります。
この問題の場合は「兄の残金は弟の残金の3倍になった」が、それです。
この文に沿って、あれこれ難しく考えず、等式をつくればいいんです。
つまりこれ。
$$860-2x=3(940-3x)$$

方程式がつくれないという生徒はよく、あれこれ難しく考えすぎていることがあります。
文に沿って素直につくっていけばいいからね。
あとはつくった方程式を解き、確かめて、答えを書くだけです。

このように「代金と個数」における残金の問題では、
①まずそれぞれの残金を \(x\) を使って表す
②等しい関係を表す文に沿って等式をつくる
この2段階に分けて考えれば解いていくことができます。
この方法で、以下、類題を解いてみてください。(答は末尾に記載)
問7)大泉君は1000円、安田君は820円持っていて、二人とも同じ本を買ったら、大泉君の残金は安田君の2倍になった。本代を求めよ。
問8)森崎君は4000円、音尾君は1500円持って買い物に行き、同じハンカチを森崎君は3枚、音尾君は1枚買ったところ、森崎君の残金は音尾君の残金の2倍より120円多くなった。ハンカチ1枚の値段を求めよ。
問9)鈴井君と戸次君はあわせて2000円持っていたが、鈴井君が800円、戸次君が300円使ったので、鈴井君の残金は戸次君の2倍になった。鈴井君ははじめ何円持っていたか求めよ。
問7)640円
問8)880円
問9)1400円
*問9)は合わせて~問題と組み合わせています。わからない場合はコメント欄から質問ください、お答えします。
ちなみにこの解き方は「分配」「年齢」「貯金」の文章問題でも利用できます。
つまり分配の問題も、年齢の問題も、貯金の問題も、ぜんぶやり方は残金の問題といっしょ。
①分配したり、年月が経ったり、貯めたり下ろしたりした後の数を \(x\) を使って表す
②文に沿って等式(=方程式)をつくる
この2段階でいけば、どんな問題でも方程式をつくることができます。
詳しくは次回の記事で解説しますね。
まとめ

〇方程式文章題の手順および基本の解き方は以下のとおり。
(1)求めるものを \(x\) とする
…単位があれば忘れずに付けること。
(2)等しい関係をみつけて方程式をつくる
…方程式をつくるときのコツは3つ
- イラストを描いてイメージする
- \(x\) の代わりに具体的な数字を入れてみる
- 何算するかを考える
(3)方程式を解く
…解く段階でつまずく場合は計算を復習すること。
(4)問題に合っているか確かめる
…一行目に解を入れて読み、おかしくないか確かめる。
…最後、答えを書くときも単位忘れに注意。
〇「代金と個数」の文章問題の解き方のコツは以下のとおり。
わからない数が2つある場合は、一方を \(x\) とし、もう一方を \(x\) を使った式で表す。
とくに「合わせて●」という問題なら、一方を \(x\) 、もう一方を ●\(-x\) と表せる。
とくに「BはAより~」という問題なら、Aを \(x\) 、Bを条件文どおりの式で表す。
また残金の問題なら、
①まずそれぞれの残金を \(x\) を使って表す
②等しい関係を表す文に沿って等式をつくる
という2段階にわけて方程式を立てるといい。
以上、方程式文章題の基本と、「代金、個数」問題の解き方のコツでした。
次回は「分配、年齢、貯金」問題のコツについて解説します。
→中学数学「1次方程式」文章題の解き方②【分配、年齢、貯金】
(数学指導法の記事一覧はまとめページへ)










コメント
問3の途中式がどうしてもわかりません。教えてください。
問8)森崎君は4000円、音尾君は1500円持って買い物に行き、同じハンカチを森崎君は3枚、音尾君は1枚買ったところ、森崎君の残金は音尾君の残金の2倍より120円多くなった。ハンカチ1枚の値段を求めよ。
上記の問いの式の立て方がわかりません。ぜひ教えてください。
4000−3x=2(1500−x)
4000~3x=3000−2x
移行したら符号変更するから4000引く3000=−2x+3x
=1000−120
X=880
ハンカチ一枚の値段は880円参考にしてくれたら嬉しいな勉強頑張ってね
残金の問題のコツがわかりません
Aノートと、それより50円高いBノートがある。Aノート3冊とBノート冊の代金の合計は600円です。Aノート1冊の値段を求めなさい。という問題の解き方を教えてください。
和田さま
Bノートが何冊か教えてください。
安田君と大泉君の問題についてですが(問7)大泉くんの残金は安田君の2倍と書かれていますが、どうして安田君に2が掛けられるのでしょうか、教えて下さいm(_ _)m
なまちさま
返信が遅くなりましたm(_ _)m
たとえば「6は3の2倍」なら
6=3×2
となります。同様に「大泉は安田の2倍」なら
(大泉の残金)=(安田の残金)×2
だからです。
問7)大泉君は1000円、安田君は820円持っていて、二人とも同じ本を買ったら、大泉君の残金は安田君の2倍になった。本代を求めよ。
の、計算方法を教えていただきたいです
>上野さま
本代をx円とすると、
1000-x=2(820-x)
1000-x=1640-2x
-x+2x=1640-1000
x=640
回答ありがとうございます。またわからない時はよろしくお願いします
先日質問させて頂いた問題の類題は、どのように解けばよいでしょうか。(共通したやり方はありますか。)
教えていただきありがとうございます。またわからないところがあったらお教えください。宜しくお願いいたします。
バス遠足に行くのに55人乗りのバスにすると最後の1台にまだ40人乗れ、65人乗りのバスにすると55人乗りよりも2台少なくて済み、空席もないといいます。そこで、65人乗りのバスで行くことにしました。バスは何台必要ですか。また、遠足に行く人数を求めなさい。
この問題の式は、65x=55(x+2)-40なのですが、いまいちよくわかりません。説明をよろしくお願い致します。
>この問題の式は、65x=55(x+2)-40なのですが、いまいちよくわかりません。
「65人乗りのバスをx台とする。」として、両辺それぞれで人数を表しています。左辺はわかりやすいと思うので、右辺の説明だけ。
(x+2):55人乗りのバスは65人乗りのバスより2台多いから。
-40:55人乗りのバスの場合、最後の1台に空席が40あるから。
詳しくは以下の記事を参照ください↓
中学数学「1次方程式」文章題の解き方⑤【過不足の問題】
問2の式が作れません。
問2の120円のかごの値段をどこに置いたらいいか分かりません。また解がりんご2個ですが、何故そうなるのか分かりません。
りんごをx個とすると、
みかんは(8-x)個と表せる。
110x+60(8-x)+120=700
これを解けば x=2 と出ます。
姉と妹の問題の式がわかりません
妹の所持金をx円とすると、
姉の所持金は3x円と表せる。
3x + x = 5200
または
妹の所持金をx円とすると、
姉の所持金は5200-x(円)と表せる。
5200-x = 3x
どちらの式でも解けます。
問3の5000円とお釣りの700円の置く場所が分かりません。
Youtubeで動画を見てはどうでしょう。
意外と参考になりますよ。
問6)4mのロープをA,B2人で分ける。BのほうをAより30cm短くするように分けると、A,Bのロープはそれぞれ何cmになるか求めよ
どうやって求めればいいですか?
Aのロープをxcmとする。
Bのロープはx-30 cmと表せる。
x+(x-30)=400
2人合わせて4m(400cm)なので、こんな方程式で求められます。
「求めるものをxとする」は導入時には確かにわかりやすくてよいと思います。
しかし、例えば、「BはAより~」の問題で「Bを求めよ」という問題のように「求めるものをx」としない方がよい問題もありますよね。
その意味では、「求めるものをxとする」のではなく「わからないものをxとする」(わからないものが複数あるときに、どれをxとしたらよいかは、「BはAより~」では「Aをx」のように、問題のパターンに応じて覚える)の方がよいかと思うのですが、いかがでしょうか?
また、「残金」問題の
①それぞれの残金をxを使って表す
②文に沿って等式(=方程式)をつくる
ですが、
生徒が、なぜ、最初に「①それぞれの残金をxを使って表す」のか、
疑問に感じることはないでしょうか?
私は以下のように教えていますが、いかがでしょうか?
①問題文から等しい関係を見つけ、それを「日本語混じりの数式」で表す
等しい関係:兄の残金は弟の残金の3倍
→(兄の残金)=(弟の残金)×3
②日本語の部分をxを使って表し、方程式をつくる
(兄の残金)は、860-2x
(弟の残金)は、940-3x
よって、860-2x=3(940-3x)
「わからないものをxとする」という表現では戸惑う中学生がいました。
サンダー様も仰るように、導入時には「求めるものをxとする」という表現がいちばん納得率が高いので、いまはこれで統一しています。
また、残金問題を2段階に分けるのは、難しいと感じる生徒に対してのアドバイスです。
この連載はそうした中学生を救う目的で書いているので、もちろん、いきなり立式できる生徒ならする必要はありません。
「日本語混じりの数式」で表す、というのもナイスな工夫ですね。
機会があればジュウゴも試してみます!
回答ありがとうございます。
やはり、はじめは「求めるものをxとする」としておき、
そうではない問題が出てきたときに、例外として教えるのがよさそうですね。
2段階、については、次回とも共通しますので、そちらに書きたいと思います。
わかりやすく勉強になりました。
テストがあるので、学習ツールに使わせていただきます。
問9)鈴井君と戸次君はあわせて2000円持っていたが、鈴井君が800円、戸次君が300円使ったので、鈴井君の残金は戸次君の2倍になった。鈴井君ははじめ何円持っていたか求めよ。
解は1400円ですが、求める式を教えてください。よろしくお願い致します。
遅くなりました。
鈴井君ははじめx 円とすると、
戸次君ははじめ2000-x 円。
よって求める式は
x-800=2(2000-x-300)
となります。
ありがとうございます。
鈴井君の残金が戸次君の2倍ですので、2000-x-800=2(x-300)
x=600で戸次君の2倍になり、2000-600=1400 答え1400円 と考えました。
これでは間違いでしょうか? 宜しくお願い致します。
「戸次君ははじめx円持っていた」とするなら、その方程式で間違いありません。
ひとつ計算が余計に必要になりますが、その方法でもOKですよ。
おそらく「BはAより~」という部分を読んで、戸次君のほうをxとされたのだと思います。
ただ問9)に限っていえば、最初に「鈴井君と戸次君はあわせて2000円持っていた」とあるので、どっちをxとしてもかまわないのです。
そのうえで、最後に「鈴井君ははじめ何円持っていたか」とあるので、「鈴井君ははじめx円持っていた」としたほうが計算がひとつラクになります。
つまり
「あわせて○なら、どちらか一方をx」
「BはAより~なら、Aをx」
これのどっちを使うかの判断は、お金を出したりして変化する前の、文章題の最初の段階で、ということです。
ありがとうございました。よく分かりました。また分からない所がありましたらお教え下さい。宜しくお願い致します。