有理化とルートの乗除につづいて、ルートの加減および展開の計算を解説します。
ルートの計算(加減)

ルートの足し算・引き算のやり方は、同類項をまとめる場合とおなじです。
ルートの加法・減法のやり方
例題5)次の計算をせよ。
$$ \mbox{(1)} \ 3 \sqrt{5} + 4 \sqrt{5} \qquad \mbox{(2)} \ 2 \sqrt{3} – 3 \sqrt{7} – 4 \sqrt{3} + 5 \sqrt{7} $$
たとえば例題5-(1)の場合、\(\sqrt{5}\) が共通です。
なので、\(3x+4x=7x\) という計算と同じようにして、
\begin{eqnarray} & & 3 \sqrt{5} + 4 \sqrt{5} \\ &=& 7 \sqrt{5} \end{eqnarray}
とできます。
また例題5-(2)の場合、\(\sqrt{3}\) と \(\sqrt{7}\) を含む項がそれぞれ2つずつあります。
なので、\(2a-3b-4a+5b=-2a+2b\) という計算と同じようにして、
\begin{eqnarray} & & 2 \sqrt{3} – 3 \sqrt{7} – 4 \sqrt{3} + 5 \sqrt{7} \\ &=& -2 \sqrt{3} + 2 \sqrt{7} \end{eqnarray}
とできます。
つまり、文字式の同類項をまとめるのと同じようにするだけ。
ちなみに、なぜこう計算していいのか?
それはどちらも、分配法則の逆をしているからですね↓
\(-2 \sqrt{3} +2 \sqrt{7}\) がこれ以上計算できないのもおなじ理由です。
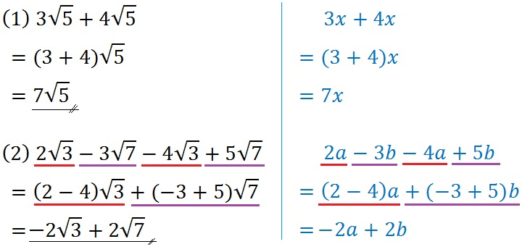
注意点
例題6)次の計算をせよ。
$$ \mbox{(1)} \ \sqrt{27} – \sqrt{48} \qquad \mbox{(2)} \ \sqrt{18} – \frac{4}{\sqrt{2}} $$
ルートの足し算・引き算における注意点も2つです。
- ルートを簡単にしてから計算
- 有理化してから計算
たとえば例題6-(1)の場合、一見するとまとめることができそうにありません。
しかし、ルートを簡単にしてやれば \(\sqrt{3}\) という共通部分が出てきて、以下のようにまとめられます。
\begin{eqnarray} & & \sqrt{27} – \sqrt{48} \\ &=& 3 \sqrt{3} -4 \sqrt{3} \\ &=& – \sqrt{3} \end{eqnarray}
また例題6-(2)の場合も、パッと見たところ、まとめられる感じではない。
しかし、\(\sqrt{18}\) を簡単にして、そして \(\frac{4}{\sqrt{2}}\) を有理化してやれば、以下のようにまとめられます。
\begin{eqnarray} & & \sqrt{18} – \frac{4 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} \\ &=& 3 \sqrt{2} – \frac{4 \sqrt{2}}{2} \\ &=& 3 \sqrt{2} -2 \sqrt{2} \\ &=& \sqrt{2} \end{eqnarray}
ルートの足し算・引き算では「ルートを簡単にしてから・有理化してから」計算すればいいと覚えておきましょう。
>Amazonプライム・ビデオ「簡単なお仕事です。に応募してみた」
ルートの計算(展開)

平方根の計算、さいごは展開です。
やり方は、展開公式に当てはめるだけです。
ルートの展開のやり方
例題7)次の計算をせよ。
(1) \( ( \sqrt{2} +3)( \sqrt{2} +4) \)
(2) \( ( \sqrt{5} -6)^2 \)
(3) \( ( \sqrt{7} +\sqrt{6} )( \sqrt{7} -\sqrt{6} ) \)
例題7-(1)はかっこの前だけそろっているので、乗法公式1
\begin{eqnarray} & & (x+a)(x+b) \\ &=& x^2 +(a+b)x +ab \end{eqnarray}
に当てはめます。
前を二乗して:\(2\)
うしろを足して、×前:\(+7 \sqrt{2} \)
うしろをかけて:\(+12\)
\begin{eqnarray} & & ( \sqrt{2} +3)( \sqrt{2} +4) \\ &=& 2+7 \sqrt{2} +12 \\ &=& 14+7 \sqrt{2} \end{eqnarray}
詳しくは→乗法公式1

また例題7-(2)はかっこの二乗の形なので、乗法公式2
\begin{eqnarray} & & (a+b)^2 \\ &=& a^2 +2ab +b^2 \end{eqnarray}
に当てはめます。
前を二乗して:\(5\)
前・うしろかけて、2倍:\(-12 \sqrt{5}\)
うしろを二乗して:\(+36\)
\begin{eqnarray} & & ( \sqrt{5} -6)^2 \\ &=& 5 -12 \sqrt{5} +36 \\ &=& 41-12 \sqrt{5} \end{eqnarray}
詳しくは→乗法公式2

そして例題7-(3)はうしろの符号だけちがう形なので、乗法公式3
\begin{eqnarray} & & (a+b)(a-b) \\ &=& a^2 -b^2 \end{eqnarray}
に当てはめます。
同符号どうしをかけて:\(7\)
異符号どうしをかけて:\(-6\)
\begin{eqnarray} & & ( \sqrt{7} +\sqrt{6} )( \sqrt{7} -\sqrt{6} ) \\ &=& 7-6 \\ &=& 1 \end{eqnarray}
詳しくは→乗法公式3
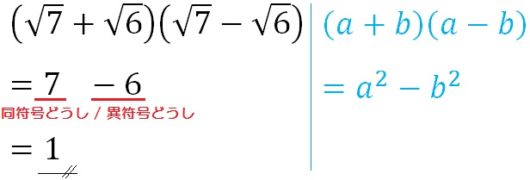
注意点
このように、ルートの展開の計算では乗法公式をスラスラ使えることが前提になります。
教科書や参考書などには説明のために
\begin{eqnarray} & & ( \sqrt{2} +3)( \sqrt{2} +4) \\ &=& (\sqrt{2})^2 +(3+4) \times \sqrt{2} +3 \times 4 \\ &=& \cdots \end{eqnarray}
などとていねいな計算式が書いてありますが、これをマネしてはいけません。
マネしてこんなん書いてたら、テスト時間内に解き終わらないから。
「前を二乗」
「うしろを足して、×前」
「うしろをかけて」
などの計算は暗算でやるようにしましょう。
例題8)次の計算をせよ。
(1) \( (2 \sqrt{2} -5)(\sqrt{8} +3) \)
(2) \( (\sqrt{3} + \sqrt{6})^2 \)
(3) \( (\sqrt{20} -2 \sqrt{3})(2 \sqrt{5} + \sqrt{12}) \)
ルートの展開における注意点はあと2つ。
- 最後まで計算する
- ルートを簡単にする
という2点を忘れないコト。
これらに注意して例題8を計算すると、以下のとおりです。
例題8がこれくらいの式の短さでスラスラ計算できるようになれば、ルートの計算はOKと思っていいでしょう。
逆に
「\(-5+3\) で \(-2\) 、これに \(2 \sqrt{2}\) をかけて、ええと…」
「\(2 \sqrt{18}=\) …、あれ、\(\sqrt{18}\) って何ルート何だっけ…」
「\((2 \sqrt{5})^2\) は、\(2 \sqrt{5} \times 2 \sqrt{5}\) だから、あれ?」
などと考えこんで、たびたび手が止まる。
こんな場合はまだ練習が不十分です。
前回までの記事を確認して、そのあと教科書や問題集でたくさん練習してください。
[平方根の記事 一覧]
- 中3数学「平方根」のコツ① 平方根とは/平方根の大小
- 中3数学「平方根」のコツ② 有理数と無理数/循環小数と分数
- 中3数学「平方根」のコツ③ 素因数分解/ルートを簡単にする計算
- 中3数学「平方根」のコツ④ 有理化/加減乗除/展開
- 中3数学「平方根」のコツ⑤ 平方根の近似値/式の値
- 中3数学「平方根」のコツ⑥ 最小の自然数n/整数部分と小数部分
まとめ

○分母の有理化は、上下に同じ数をかける。
注意点は、有理化したあとの約分を忘れないこと。
○ルートの乗除は、ルートの中どうし・外どうしを計算する。
注意点は、数がでかくなりそうならルートの中身を素因数分解してもいい。
また、わり算は分数になおすこと。
○ルートの加減は、同類項をまとめるように。
注意点は、有理化してからまとめたりすること。
○ルートの展開は、乗法公式に当てはめる。
注意点は、乗法公式をスラスラ使えるようになっておくこと。
また、最後まで計算できるところは計算すること。
そしてルートの計算ではすべて、ルートを簡単にしてから計算すること。
以上、ルートの基本計算でした。
次回と次々回は中3平方根単元の最後として、平方根の利用・応用問題を解説します。
定期テストや模試・入試でよく出る難問をどうやって解けばいいか、パターンにわけてコツをお伝えしていきます。


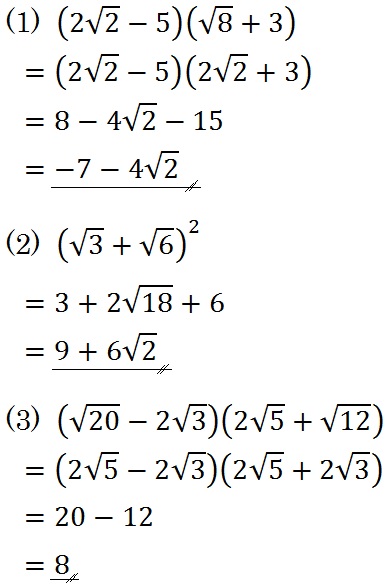
コメント