中学数学の教え方について、具体的に解説するこの連載。
今回から中2「連立方程式」単元に入ります。
この連立方程式単元は、今後の生徒の数学力を左右するおおきな山場のひとつです。にもかかわらず、「思考力」とか「深い理解」とか言って具体例や理屈をこねくり回し、肝心のところが抜け落ちた指導をよく見かけます。
連立方程式でもっとも身につけさせるべき能力とは何か?
そのためにどんな指導がもっとも効果的なのか?
中学生を教えるすべての方にご参考ください。
[前の記事]中2数学「等式の変形」の教え方
[次の記事]中2数学「連立方程式」加減法つづき
(数学指導法の記事一覧はまとめページへ)
連立方程式を通して養うべき力

中学2年生の春から夏にかけて学校で習う連立方程式。
子どもたちがこれからも数学好き・数学できる人となるために、この単元でもっとも養うべき能力とは何か?
それは記述式の解答を論理だてて書ききる力です。
数学が得意になるかの分岐点
上図の問題・解答例を見てもわかるとおり、連立方程式を解くには長ーい記述が必要です。
連立方程式では、式の計算・1次方程式・代入といった学習済みの知識をいろいろ組み合わせて書かなくてはいけません。また「ここでどんな計算をしたのか」という言葉も、あいだあいだに挟まなくてはいけません。
これが十分にできない中学生は、これから先、数学が苦手になります。
なぜなら、パッと答えが浮かぶ問題以外はぜんぶ「むずかしい」と感じるようになるからです。
つまり、長い論理的思考が必要な問題はすべて、できなくなってしまいます。
結果として、
- 「図形の証明」
- 「方程式 文章題」
- 「関数の利用」
- 「複雑な確率問題」
など、およそ模試や入試や定期テストで出されるあらゆる問題がぜんぶ太刀打ちできなくなります。
その結果、高校受験時の選択肢は限られてきます。「小問集合だけカンペキに解いて、あとは運まかせ」というスタンスで望むしかなくなるからです。
また高校入試はなんとかなって、平均以上の高校に進学したけれど、高校数学にはまったくついていけず、記述問題は定期テストでも模試でもボロボロ。こんな生徒もたくさん見てきました。
みな、記述式の解答を論理的に書ききる力がないからです。
中3ならまだなんとか矯正できた子もいますが、高校生になるともう自分のクセがついてしまって、よほど本人のなかで意識改革が起こらないかぎりはムリでした。
いかに連立方程式の導入が大切か。
つまりここで、他人にわかりやすく説明するような解答を書けるようになるのか。
それとも「答えさえ出りゃいい」というスタンスのまま2学期を迎えるのか。
連立方程式という単元はその分岐点だと、中学数学の指導にあたる者はまず心得るべきだと考えます。
不要な指導いろいろ
なので、連立方程式の導入においては、「記述式の解答を論理だてて書ききる力」の育成にポイントをしぼって、指導にあたるといいでしょう。
よって、教科書にあるような具体例などは不要です。
りんごとかアメとか、鶴亀算とか、はては生徒自身に具体例を考えさせたりとか、そんな授業で数学の有用性が実感できるでしょうか?
わたしたちが「数学ってこんな役に立つんだ」と実感するのは、大学以降の、高等数学を自由自在に使えるようになった後の話です。この連載で何回も書いてますが、中学・高校数学においては、まずびしーっとやり方を示してできるようにさせること。意味とか理屈とか教えるのはそのあとにしましょう。

また、解き方を示す前に「考え方としては \(y\) を消去して \(x\) だけの一次方程式にする」とかの説明も不要です。
そんな説明は、生徒が実際に解き方を理解した後じゃないと、イメージをともなって理解できないからです。同じ理由で「加減法とは」「等式の性質とは」などの前口上も要りません。
そして、連立方程式を解いている最中に既習の知識を解説しだす、これも混乱をきたす原因です。
たとえば式どうしの引き算の筆算をつくってから、「引き算だから、\(y -(-3y) \) となるから…」みたいな説明とか。「\(3x=5\) 、この1次方程式を解くには、両辺に \(\frac{1}{3}\) をかければよかったね」とか。
こういうその場その場での復習が、記述式の解答を一気に書くという姿勢から生徒を遠ざけることになります。
したがって、既習の知識の復習は連立方程式に入る前にぜんぶ済ませてしまう。この指導順をおすすめします。
効果的な指導順
では、ジュウゴのおすすめする最短かつ効果的な指導とは何か。
以下の内容と順番です。
1.復習をする
- 1次方程式
- 式の値(代入)
- 式の加減の筆算
2.連立方程式とは何かの説明
- 文字が2つで等式も2つだ
- 加減法と代入法って解き方がある
3.加減法の導入(たし算)
- 解答を示してから、解説
- 書き写させてから、類題
4.加減法の導入(ひき算)
- 解答を示してから、解説
- 書き写させてから、類題
- 練習問題をさせてみる
5.加減法つづき(一方だけ係数をそろえる)
- 解答を示してから、解説
- 書き写させてから、類題
- 練習問題をさせてみる
6.加減法つづき(両方とも係数をそろえる)
- 解答を示してから、解説
- 書き写させてから、類題
- 練習問題をさせてみる
7.まとめと練習
以上1~7の内容をだいたい2時間くらいで指導します。
塾や予備校、家庭教師などで時間のない方。
またわが子に「連立方程式を教えてー」とせがまれた保護者の方。
これから実際の指導案を書いていきますのでぜひ参考にしてください。
*連立方程式の文章題はこちら
1.復習をする

まずは「これからの単元で必要な知識だから」と言って、復習をさせます。
連立方程式を一気に解くために必要な力はあるか、チェックすると同時に、忘れているようなら必要量を練習させてください。
復習する内容はぜんぶで3つです。
1次方程式
$$ 3x=18 \quad -12y=60 $$
$$ 7x=2 \quad 8y=-36 $$
$$ 5x-2=3x+4 $$
$$ 8y-3(2y-1)=9 $$
$$ 0.7x+4=1.5x $$
$$ \frac{1}{4}y – \frac{5}{6} = \frac{1}{2} – \frac{2}{3}y $$
以上8問がすべて解ければ、1次方程式はOKです。
解けない場合は50問でも100問でも復習しましょう。
1次方程式の解き方については過去記事もご参照ください↓
式の値(代入)
\(x=-5\) 、\(y=\frac{1}{2}\) のとき、次の式の値を求めよ。
$$3x \qquad -5x+7$$
$$8y \qquad 4x-6y$$
$$2x-9y-6x+5y$$
$$4(x-2y)-5(3x-y)$$
以上6問がすべて解ければ、代入もOKです。
解けない場合は50問でも100問でも復習しましょう。
式の加減の筆算
\begin{eqnarray} 7x &+&2y \\ +) \ 3x &-&6y \\ \hline \end{eqnarray}
\begin{eqnarray} -8x &-&5y \\ +) \ x &-&9y \\ \hline \end{eqnarray}
\begin{eqnarray} 4x &+&7y \\ -) \ 3x &-&10y \\ \hline \end{eqnarray}
\begin{eqnarray} -x &-&6y \\ -) \ 5x &-&2y \\ \hline \end{eqnarray}
以上4問がすべて解ければ、式の加減の筆算もOKです。
解けない場合は50問でも100問でも復習しましょう。
なお引き算の場合、「下段の符号をぜんぶ逆にする」というコツがあります。難しがる生徒にはご参考ください。
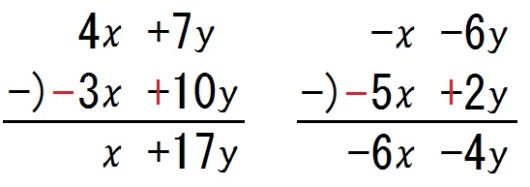
以上の復習を終えてから、連立方程式の導入に入ります。
2.連立方程式とは何か

連立方程式とはどういうものか。
簡潔に、わかりやすく伝えましょう。
文字が2つで等式も2つ
問題)■+▲=\(5\)
■と▲に当てはまる整数の組はなーんだ?
(生徒に答えさせていく)。
そうだね、
(1,4)(2,3)(3,2)(4,1)(5,0)
(0,5)(-1,6)(-2,7)…限りなくあるね。
では、これらの答えの中で、
■ー▲=\(3\) にも当てはまるものはなーんだ?
そう、(4,1)だ。
つまり
\begin{eqnarray} \left\{ \begin{array}{l} \mbox{■}+ \mbox{▲} = 5 \\ \mbox{■}- \mbox{▲} = 3 \end{array} \right.\end{eqnarray}
この2つの等式を同時に満たす答えは
ただ1組だ。
■と▲の代わりに \(x\) と \(y\) を使うと、
\begin{eqnarray} \mbox{(問題)}\left\{ \begin{array}{l} x+y = 5 \\ x-y = 3 \end{array} \right.\end{eqnarray}
$$ \mbox{(解答)} \ x=4 , y=1 $$
こんなふうに、等式(方程式)が2つあって、両方に当てはまる \(x\) と \(y\) の正体を探す、これを連立方程式という。
この連立方程式をこれから学習していきます。
ちなみに、\(x+y=5\) とか \(x-y=3\) という方程式は「文字が2つで、どっちも次数は1次」だから2元1次方程式という。
だから中1で習った \(x+2=5\) などは「文字が1つで次数も1次」だから、正確にいうと1元1次方程式。中3で習う \(x^2 =9\) とかは1元2次方程式、です。
あと、連立方程式の答えは分数になることもあるからね。
[関連記事]
中1「1次方程式」でつまずく原因と解決法④ 分数
加減法と代入法
では、連立方程式というパズルを解くにはどうしたらいいか?
当てずっぽうで解くしかないのか?
いや、どんな連立方程式でも絶対に解ける方法がある。しかも2つ。
ひとつは加減法。
もうひとつは代入法。
まずは加減法のやり方から説明するよ。
最終的にはどっちの方法で解いてもいいんだけどね。
3.加減法の導入(たし算)

ではいよいよ加減法の導入です。
解答を示してから、解説
\begin{eqnarray} \left\{ \begin{array}{l} 7x+3y = 26 \\ 5x-3y = -2 \end{array} \right.\end{eqnarray}
たとえばこの連立方程式を、加減法で解いてみせます。
よーく見ててくれ。
\begin{eqnarray} \left\{ \begin{array}{l} 7x+3y = 26 \ \large{\mbox{…①}} \\ 5x-3y = -2 \ \large{\mbox{…②}} \end{array} \right.\end{eqnarray}
①+②をして
\begin{eqnarray} 7x +3y &=& 26 \\ +) \ 5x -3y &=& -2 \\ \hline 12x \qquad &=& 24 \\ x &=& 2 \ \large{\mbox{…③}} \end{eqnarray}
③を①に代入して
\begin{eqnarray} 14 +3y &=& 26 \\ 3y &=& 26 -14 \\ 3y &=& 12 \\ y &=& 4 \end{eqnarray}
答.\(x=2 , y=4\)
さて、いま何をしたのか解説するね。
まず2つの式に①②と番号をふった。
んで①と②の式を筆算でたし算した。
すると \(12x=24\) となり、\(y\) が消えた。
なぜか?
\(y\) の係数が、①式は \(+3\) 、②式は \(-3\) だったからだ。
つまり数字が同じで符号が逆なら、式どうしをたし算すれば、その文字が消去できるんだ。
そしたら、\(12x=24\) はただの1元1次方程式だから、解いて、\(x=2\) 。
こうしてまず、片方の文字の正体がわかる。

\(x\) の正体が \(2\) とわかったら、次にそいつを①式または②式に代入する。
これはどっちに代入してもいい。自分のお好みで。
たとえば①式に代入した場合、\(14+3y=26\) 。
これも、\(y\) についてのただの1元1次方程式だ。だから解ける。
解いたら \(y=4\) が出て、これで両方の正体がわかった。
最後に「 \(x=2 , y=4\) 」と、両方の正体をそろえて書いて、答えとなる。

ちなみに \(x=2\) を②に代入しても、以下のように同じ答えになるからね。
③を②に代入して
\begin{eqnarray} 10 -3y &=& -2 \\ -3y &=& -2 -10 \\ -3y &=& -12 \\ y &=& 4 \end{eqnarray}
書き写させてから、類題
つまり加減法とは、
- 数字が同じで符号が逆、そんな係数があったら式どうしをたし算して、文字をひとつ消去する。
- 残った文字についての方程式を解いて、片方の正体を出す。
- その正体を①か②に代入して、また方程式を解いて、もう片方の正体も出す。
こんな方法のこと。
理解したら、解答をすべて書き写してもらう。
写すときの注意点は以下3つ。
- どんな計算をしたのか、ことばを必ず書く。
- 式どうしの筆算のときや方程式を解くとき、=を縦にそろえるときれい。
- 答えの形は教科書によっては \((x,y)=(2.4)\) などの場合もある。学校に従おう。
では、類題を一緒に解いてみよう。
\begin{eqnarray} \left\{ \begin{array}{l} x-4y = -5 \\ 3x+4y = -7 \end{array} \right.\end{eqnarray}
\begin{eqnarray} \left\{ \begin{array}{l} x-4y = -5 \ \large{\mbox{…①}} \\ 3x+4y = -7 \ \large{\mbox{…②}} \end{array} \right.\end{eqnarray}
①+②をして
\begin{eqnarray} x -4y &=& -5 \\ +) \ 3x +4y &=& -7 \\ \hline 4x \qquad &=& -12 \\ x &=& -3 \ \large{\mbox{…③}} \end{eqnarray}
③を①に代入して
\begin{eqnarray} -3 -4y &=& -5 \\ -4y &=& -5 +3 \\ -4y &=& -2 \\ y &=& \frac{1}{2} \end{eqnarray}
答.\(x=-3 , y=\frac{1}{2} \)
長くなったので、つづきは次回。
*連立方程式の記事一覧
- 導入と指導上の注意点
- 加減法のつづき
- 代入法
- 小数・分数問題
- 文章題1(立式のコツ)
- 文章題2(整数や過不足問題など)
- 文章題3(道のり問題)
- 文章題4(割合の問題)









コメント
このサイトが上に来てしまうのがやばいなと思いました。
いかにも塾っぽい考え方ですね。教育学を学んで教科書研究をしたらこんな考え方にはならないです。あくまで持論ということだとは思いますが。
教育学を学んで、現行の指導要領などに沿った指導なら、このような教え方にならないのはわかりますが、結局学校によって学力に差があり、色々な意味での困難校なら探究的や対話的が成り立たないような場合もあると思います。基礎基本がなっていない人間に課題探究なんでやらせても、結局何ができるようになったのかわからず、知識思考は散漫になるので、そういう生徒向けにはよいと思います。
すみません、名前を入力せずに送信してしまったので、念のため再送します。
記述式の解答を論理だてて書ききる力、が大切なのはその通りだと思います。
ただ、上記の連立方程式程度の問題だと、てきとーにやっても答えが出せてしまうので、
てきとーにやってしまう生徒が多いです。
じゅうごさんは、そのようなてきとーにやってしまう生徒に対して、どのように対応していますか?
>てきとーにやってしまう生徒に対して、どのように対応していますか?
答えだけ合っていても途中の解答に不備があるなら✓にします。
記述式の解答を論理だてて書ききる力、が大切なのはその通りだと思います。
ただ、上記の連立方程式程度の問題だと、てきとーにやっても答えは出せてしまいますよね。
なので、てきとーにやってしまう生徒が多いです。
じゅうごさんは、そのようなてきとーにやってしまう生徒に対して、どのように対応していますか?